5 5/6 As A Decimal
straightsci
Sep 13, 2025 · 5 min read
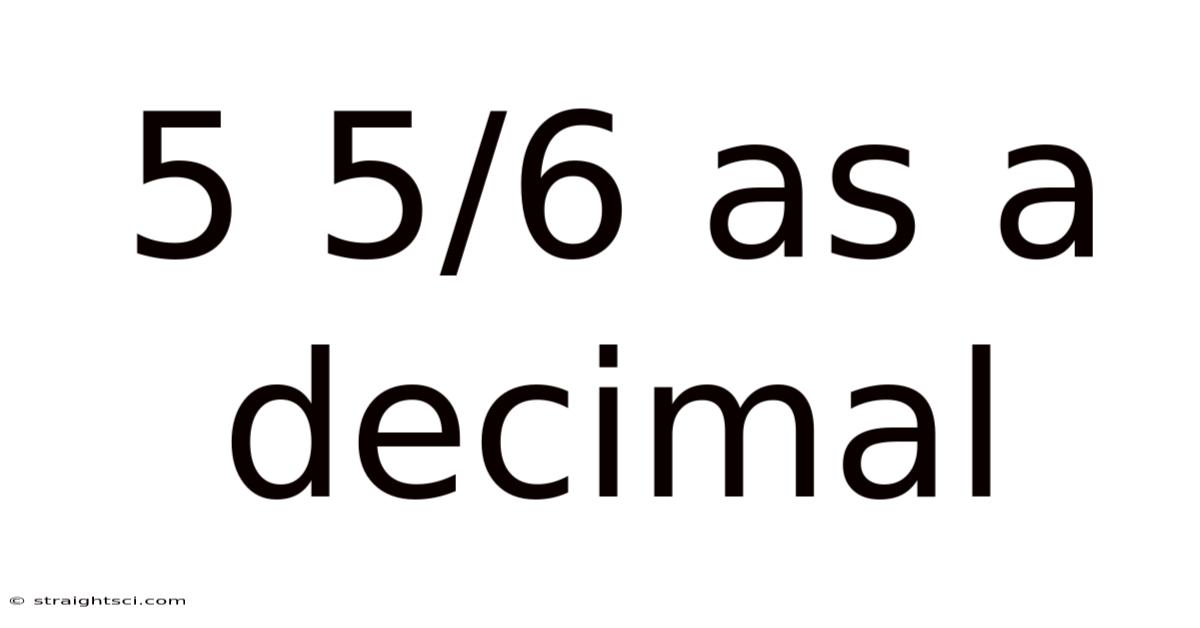
Table of Contents
5 5/6 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide delves into the process of converting the mixed number 5 5/6 into its decimal equivalent, explaining the methodology step-by-step and exploring the underlying mathematical principles. Understanding this conversion is not just about getting the right answer; it's about grasping the relationship between fractions and decimals, a key concept in numeracy. We'll cover the process, explore alternative methods, and answer frequently asked questions to solidify your understanding.
Understanding Fractions and Decimals
Before diving into the conversion, let's briefly review the concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 5/6, 5 is the numerator and 6 is the denominator. A decimal, on the other hand, represents a part of a whole using the base-ten number system. The decimal point separates the whole number part from the fractional part. For instance, 0.75 represents seventy-five hundredths.
The key to converting between fractions and decimals lies in understanding that both represent portions of a whole. The denominator of a fraction dictates the place value in the decimal representation.
Converting 5 5/6 to a Decimal: The Step-by-Step Method
The mixed number 5 5/6 consists of a whole number part (5) and a fractional part (5/6). To convert this to a decimal, we'll handle each part separately and then combine them.
Step 1: Convert the Fraction to a Decimal
The core of the conversion lies in transforming the fraction 5/6 into its decimal equivalent. We achieve this through division:
- Divide the numerator by the denominator: Divide 5 by 6. This gives us 0.83333... The three dots indicate that the decimal is recurring or repeating; the digit 3 repeats infinitely.
Step 2: Combine the Whole Number and Decimal Parts
Now that we have the decimal equivalent of the fractional part (0.83333...), we simply add it to the whole number part (5):
- Add the whole number and the decimal: 5 + 0.83333... = 5.83333...
Therefore, 5 5/6 as a decimal is approximately 5.8333. The recurring 3 necessitates rounding depending on the desired level of precision. For most practical purposes, rounding to a few decimal places (e.g., 5.833) is sufficient.
Alternative Methods: Understanding Long Division
While the previous method provides a quick overview, a deeper understanding involves exploring long division – the process behind the conversion. Let's illustrate this with the fraction 5/6:
0.8333...
6 | 5.0000
4.8
0.20
0.18
0.020
0.018
0.0020
0.0018
0.0002
As you can see, the division results in a recurring decimal, 0.8333... This emphasizes that some fractions do not have exact finite decimal representations.
Understanding Recurring Decimals
The recurring decimal 0.8333... is a specific type of decimal known as a repeating decimal or recurring decimal. It's characterized by a sequence of digits that repeat indefinitely. These decimals are often represented using a bar over the repeating digits (e.g., 0.8̅3̅) or by specifying the repeating block. Understanding recurring decimals is essential because many fractions produce them upon conversion.
Practical Applications of Decimal Conversion
Converting fractions to decimals is a fundamental skill with broad applications across various fields:
- Everyday calculations: Sharing bills, calculating discounts, measuring ingredients in recipes, and many other daily activities involve fractional and decimal representations.
- Science and engineering: Precise measurements and calculations in physics, chemistry, and engineering often necessitate converting between fractions and decimals for accuracy and consistency.
- Financial calculations: Interest rates, stock prices, and various financial transactions often involve decimal representations of fractions.
- Computer programming: Many programming languages require numerical inputs in decimal format, making fraction-to-decimal conversion crucial for certain algorithms and computations.
Frequently Asked Questions (FAQ)
Q1: Why is 5/6 a recurring decimal?
A1: The reason 5/6 results in a recurring decimal is due to the denominator (6). When the denominator of a fraction contains prime factors other than 2 and 5 (the prime factors of 10), it will typically result in a recurring decimal. Since 6 has a prime factor of 3, the decimal representation is non-terminating (recurring).
Q2: How can I round recurring decimals effectively?
A2: The most common rounding method involves determining the desired precision (number of decimal places) and then examining the digit immediately following. If this digit is 5 or greater, round up; otherwise, round down. For instance, rounding 5.83333... to three decimal places gives 5.833.
Q3: Are there other ways to convert mixed numbers to decimals?
A3: Yes, you can first convert the mixed number to an improper fraction and then divide the numerator by the denominator. For 5 5/6, you would first convert it to (5*6 + 5)/6 = 35/6, and then perform the division 35/6 = 5.8333...
Q4: What if I need more precision in my decimal conversion?
A4: While rounding is commonly used for practical purposes, some applications might require higher precision. For those cases, software or calculators with higher precision capabilities can provide more decimal places. You can represent the recurring decimal using the bar notation (0.8̅3̅) to indicate the infinite repetition.
Q5: How does this relate to percentage calculations?
A5: Decimals are directly related to percentages. To convert a decimal to a percentage, you multiply it by 100 and add a percent sign (%). For example, 0.8333... is approximately 83.33%. This connection makes decimal conversion essential for understanding and working with percentages.
Conclusion
Converting 5 5/6 to a decimal, yielding approximately 5.8333, is a straightforward process involving the division of the numerator by the denominator and the addition of the whole number part. However, the process also highlights crucial mathematical concepts such as fractions, decimals, recurring decimals, and the significance of long division. Understanding these concepts enhances not only your ability to perform this specific conversion but also your overall mathematical proficiency. This skill forms the foundation for more advanced mathematical computations and has widespread practical applications in various fields. By grasping the methods and principles outlined in this guide, you can confidently tackle similar conversions and apply this knowledge in diverse contexts. Remember that understanding why a process works, rather than just how it works, is critical for building a strong and enduring grasp of mathematics.
Latest Posts
Latest Posts
-
1 1 7 As A Decimal
Sep 13, 2025
-
Derivative Ln X 2 1
Sep 13, 2025
-
Simple Machines In Rube Goldberg
Sep 13, 2025
-
Cheats For The Impossible Quiz
Sep 13, 2025
-
Whats The Formula For Volume
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 5 5/6 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.