Derivative Ln X 2 1
straightsci
Sep 13, 2025 · 6 min read
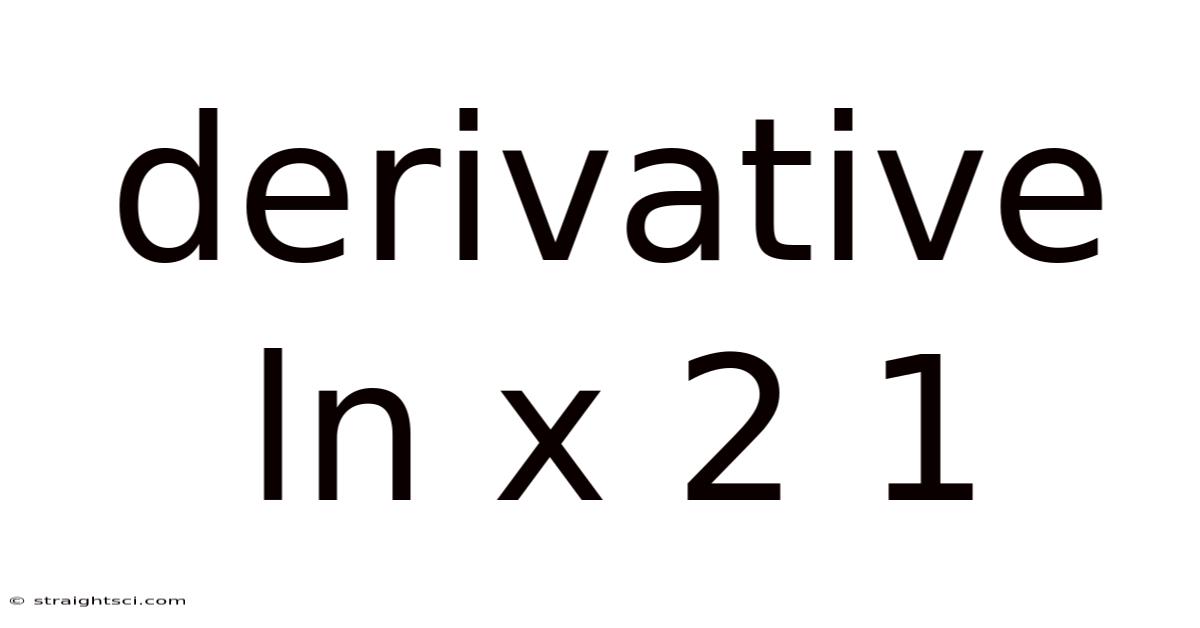
Table of Contents
Unveiling the Mysteries of the Derivative of ln(x² + 1): A Comprehensive Guide
Understanding derivatives is crucial in calculus and numerous scientific fields. This article delves into the intricacies of finding the derivative of ln(x² + 1), a common function encountered in various mathematical applications. We'll explore the process step-by-step, providing a clear and comprehensive explanation suitable for students and anyone interested in deepening their understanding of calculus. We'll also delve into the underlying principles and practical applications of this derivative.
Introduction: Understanding Derivatives and Logarithmic Functions
Before diving into the specifics of finding the derivative of ln(x² + 1), let's establish a foundational understanding of derivatives and logarithmic functions.
A derivative, in simple terms, measures the instantaneous rate of change of a function. Geometrically, it represents the slope of the tangent line to the function's graph at a specific point. The process of finding a derivative is called differentiation.
Logarithmic functions, specifically natural logarithms (denoted as ln), are inverses of exponential functions. The natural logarithm of a number x, denoted as ln(x), is the exponent to which the mathematical constant e (approximately 2.718) must be raised to obtain x. The natural logarithm is defined only for positive values of x.
The key rules we will use for differentiation are:
- Chain Rule: If we have a composite function, f(g(x)), its derivative is f'(g(x)) * g'(x). This rule is essential for differentiating complex functions.
- Derivative of ln(x): The derivative of ln(x) with respect to x is 1/x.
- Derivative of xⁿ: The derivative of xⁿ with respect to x is nxⁿ⁻¹.
- Derivative of a Constant: The derivative of a constant is 0.
Step-by-Step Calculation of the Derivative of ln(x² + 1)
Now, let's tackle the derivative of ln(x² + 1). We'll employ the chain rule, as we have a composite function: the natural logarithm of a function of x (x² + 1).
-
Identify the Outer and Inner Functions: Our composite function is ln(u), where u = x² + 1. The outer function is ln(u), and the inner function is u = x² + 1.
-
Find the Derivative of the Outer Function: The derivative of ln(u) with respect to u is 1/u.
-
Find the Derivative of the Inner Function: The derivative of u = x² + 1 with respect to x is 2x.
-
Apply the Chain Rule: According to the chain rule, the derivative of ln(x² + 1) is the derivative of the outer function (1/u) multiplied by the derivative of the inner function (2x). Substituting u = x² + 1, we get:
d/dx [ln(x² + 1)] = (1/(x² + 1)) * (2x) = 2x / (x² + 1)
Therefore, the derivative of ln(x² + 1) is 2x / (x² + 1).
A Deeper Dive: Understanding the Result
The result, 2x / (x² + 1), provides valuable insights into the behavior of the original function, ln(x² + 1). Let's analyze it:
-
The numerator (2x): This term indicates that the derivative is positive when x is positive and negative when x is negative. This means the function ln(x² + 1) is increasing for positive x values and decreasing for negative x values.
-
The denominator (x² + 1): This term is always positive because x² is always non-negative, and adding 1 ensures it's always greater than zero. This means the derivative is always defined for all real numbers x.
Applications of the Derivative
The derivative of ln(x² + 1) has significant applications in various fields:
-
Optimization Problems: In calculus, derivatives are essential for finding maximum and minimum values of functions. The derivative we calculated can be used to find critical points of the ln(x² + 1) function, helping to solve optimization problems.
-
Physics and Engineering: Many physical phenomena are modeled using logarithmic functions. The derivative aids in understanding the rate of change of these phenomena. For example, it might represent the rate of change of a quantity related to a process described by a logarithmic function.
-
Economics and Finance: Logarithmic functions and their derivatives are extensively used in financial modeling, analyzing growth rates, and understanding the behavior of various economic variables. For instance, it might represent the rate of change of a quantity related to a logarithmic growth model.
-
Computer Science: The derivative could be used in algorithm development, specifically in areas involving optimization and machine learning.
-
Statistics and Probability: Logarithmic functions are used in various statistical distributions. Their derivatives can be used to solve problems related to probability density functions and other statistical concepts.
Illustrative Examples
Let's consider a few examples to solidify our understanding:
Example 1: Find the slope of the tangent line to the curve y = ln(x² + 1) at x = 1.
To find the slope, we evaluate the derivative at x = 1:
2(1) / (1² + 1) = 2 / 2 = 1
The slope of the tangent line at x = 1 is 1.
Example 2: Find the critical points of y = ln(x² + 1).
Critical points occur where the derivative is zero or undefined. Since the denominator (x² + 1) is always positive, the derivative 2x / (x² + 1) is only zero when 2x = 0, which means x = 0. Therefore, the only critical point is at x = 0.
Frequently Asked Questions (FAQ)
Q: Why is the natural logarithm used instead of other logarithms?
A: While other logarithms could be used, the natural logarithm (base e) simplifies calculations due to its convenient properties in calculus. Its derivative is particularly straightforward.
Q: What if the function was ln(ax² + b), where 'a' and 'b' are constants?
A: The chain rule would still apply. The derivative would be (2ax) / (ax² + b).
Q: Can the derivative be negative?
A: Yes. The derivative 2x / (x² + 1) is negative when x is negative.
Q: What is the second derivative of ln(x² + 1)?
A: To find the second derivative, we differentiate the first derivative:
d²/dx² [ln(x² + 1)] = d/dx [2x / (x² + 1)] = (2(x² + 1) - 2x(2x)) / (x² + 1)² = (2 - 2x²) / (x² + 1)²
Conclusion: Mastering the Derivative of ln(x² + 1)
This comprehensive guide has explored the derivative of ln(x² + 1), providing a step-by-step explanation, deeper analysis of the results, illustrative examples, and answers to frequently asked questions. Mastering this derivative is a crucial step in building a strong foundation in calculus. Understanding the process and the implications of the result opens doors to solving various problems across numerous disciplines. Remember, the key is to practice and apply these concepts to solidify your understanding. With consistent effort, you can confidently tackle more complex derivative problems and unlock the power of calculus in your academic pursuits and professional endeavors.
Latest Posts
Latest Posts
-
6 X 9 X 2
Sep 13, 2025
-
Name Of The Thigh Muscle
Sep 13, 2025
-
Animals In Temperate Coniferous Forest
Sep 13, 2025
-
Jj Thomson Plum Pudding Experiment
Sep 13, 2025
-
What Is The Pioneer Species
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Derivative Ln X 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.