1 1/7 As A Decimal
straightsci
Sep 13, 2025 · 6 min read
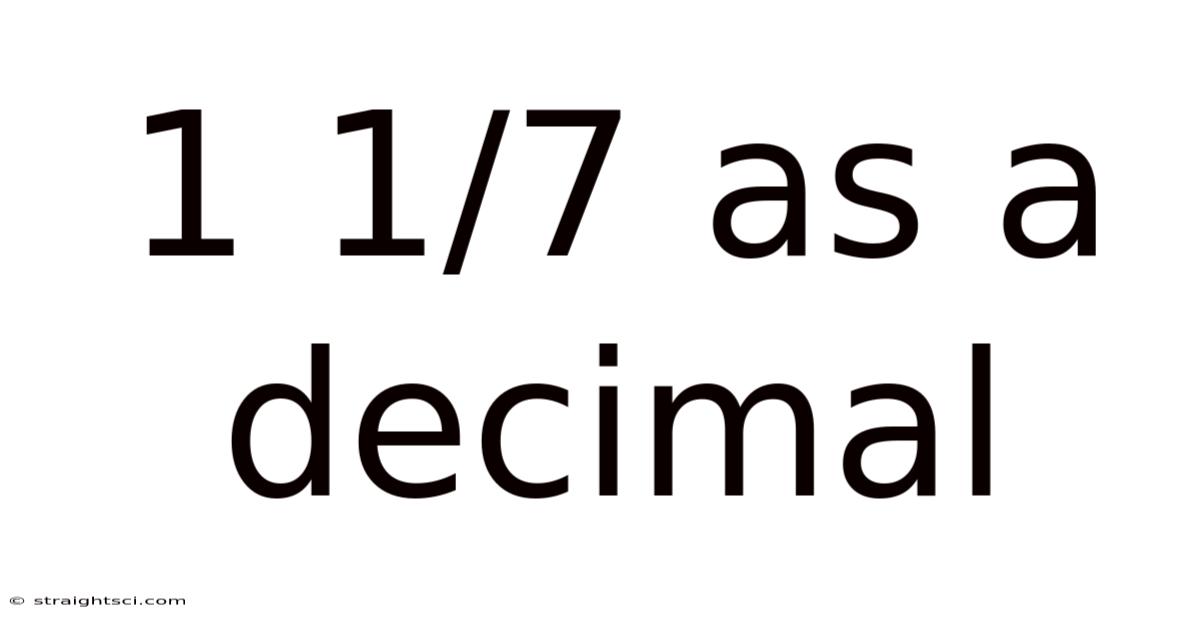
Table of Contents
1 1/7 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the mixed number 1 1/7 into its decimal equivalent, exploring various methods and delving into the underlying mathematical principles. We'll also address common questions and misconceptions surrounding decimal representation of fractions. By the end, you'll not only know the decimal value of 1 1/7 but also possess a deeper understanding of fraction-to-decimal conversion.
Understanding Fractions and Decimals
Before we dive into the conversion, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 1/7, 1 is the numerator and 7 is the denominator. This means we have one part out of seven equal parts.
A decimal, on the other hand, represents a number using a base-ten system. The decimal point separates the whole number part from the fractional part. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For instance, 0.5 represents five-tenths, or 5/10, while 0.125 represents one hundred twenty-five thousandths, or 125/1000.
Converting 1 1/7 to a Decimal: Method 1 - Long Division
The most straightforward method for converting a fraction to a decimal is through long division. Since 1 1/7 is a mixed number (a whole number and a fraction), we first convert it into an improper fraction.
Step 1: Convert the mixed number to an improper fraction.
To do this, we multiply the whole number (1) by the denominator (7) and add the numerator (1). This result becomes the new numerator, while the denominator remains the same.
1 1/7 = (1 * 7 + 1) / 7 = 8/7
Step 2: Perform long division.
Now, we divide the numerator (8) by the denominator (7).
1.142857...
7 | 8.000000
-7
10
-7
30
-28
20
-14
60
-56
40
-35
50
-49
10
-7
3...
As you can see, the division results in a repeating decimal. The digits 142857 repeat infinitely. We can represent this using a bar over the repeating sequence: 1.1̅4̅2̅8̅5̅7̅.
Therefore, 1 1/7 as a decimal is approximately 1.142857. The "..." indicates that the decimal continues to repeat indefinitely.
Converting 1 1/7 to a Decimal: Method 2 - Using a Calculator
A simpler, albeit less insightful, method is to use a calculator. Simply enter 8 ÷ 7 and the calculator will display the decimal equivalent, which will likely show a truncated version of the repeating decimal, like 1.142857142857... While convenient, this method doesn't illustrate the underlying mathematical principles involved.
Understanding Repeating Decimals
The decimal representation of 1 1/7 is a repeating decimal, also known as a recurring decimal. This means the decimal part doesn't terminate but rather repeats a specific sequence of digits infinitely. Not all fractions result in repeating decimals; some terminate (e.g., 1/4 = 0.25). Whether a fraction results in a terminating or repeating decimal depends on the denominator's prime factorization. If the denominator's prime factorization only contains 2s and/or 5s, the decimal will terminate. Otherwise, it will repeat.
The Significance of Repeating Decimals
Repeating decimals are significant because they highlight the limitations of representing rational numbers (fractions) using a finite number of decimal places. While we can approximate a repeating decimal by truncating it to a certain number of decimal places, we're always losing some degree of accuracy. The true value of the decimal representation of 1 1/7 is infinitely long.
Practical Applications and Rounding
In real-world applications, we often need to round repeating decimals to a specific number of decimal places. The level of precision required depends on the context. For example:
- Engineering: High precision is crucial, requiring many decimal places.
- Finance: Depending on the application (e.g., currency conversion), rounding to two decimal places is often sufficient.
- Everyday Calculations: Rounding to a few decimal places is typically enough.
For 1 1/7, rounding to different decimal places gives us:
- One decimal place: 1.1
- Two decimal places: 1.14
- Three decimal places: 1.143
- Four decimal places: 1.1429
- Five decimal places: 1.14286
The choice of rounding depends on the desired accuracy. It's important to be aware that rounding introduces a small error, but often this error is acceptable in practical situations.
Frequently Asked Questions (FAQ)
Q1: Why does 1 1/7 result in a repeating decimal?
A1: Because the denominator (7) in the fraction 8/7 does not have only 2 and/or 5 as its prime factors. Its prime factorization is simply 7.
Q2: Can all fractions be expressed as decimals?
A2: Yes, all fractions can be expressed as decimals, either as terminating decimals or as repeating decimals.
Q3: Is there a way to predict if a fraction will result in a repeating or terminating decimal without performing the division?
A3: Yes, by examining the prime factorization of the denominator. If the denominator's prime factorization contains only 2s and/or 5s, the decimal will terminate. Otherwise, it will repeat.
Q4: What's the difference between truncating and rounding a decimal?
A4: Truncating involves simply cutting off the decimal after a certain number of places. Rounding involves considering the next digit; if it's 5 or greater, we round up; otherwise, we round down.
Q5: How can I convert a repeating decimal back into a fraction?
A5: This involves algebraic manipulation. Let's take the repeating decimal 0.333... Let x = 0.333... Multiplying by 10 gives 10x = 3.333... Subtracting x from 10x results in 9x = 3, which simplifies to x = 1/3. This method can be extended to other repeating decimals, although the algebra can become more complex for longer repeating sequences.
Conclusion
Converting fractions to decimals is an essential mathematical skill with various applications. We've explored two methods for converting 1 1/7 into its decimal equivalent: long division, which demonstrates the underlying mathematical process, and using a calculator, which provides a quicker solution. We've also discussed the significance of repeating decimals, their practical implications, and how to handle them in real-world scenarios. Understanding these concepts not only helps in solving mathematical problems but also provides a deeper appreciation for the relationship between fractions and decimals. Remember that while calculators are helpful, understanding the underlying principles is key to mastering this fundamental mathematical concept. By utilizing long division, we can not only find the answer but also appreciate the beauty of mathematical processes and the intricate relationships between different number systems.
Latest Posts
Latest Posts
-
Identical Twins Female And Male
Sep 13, 2025
-
2x 5x 10
Sep 13, 2025
-
Freakshow In Harold And Kumar
Sep 13, 2025
-
What Do Hammer Sharks Eat
Sep 13, 2025
-
What Is A Branch Circuit
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 1 1/7 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.