X 2 Y 2 Y
straightsci
Sep 02, 2025 · 5 min read
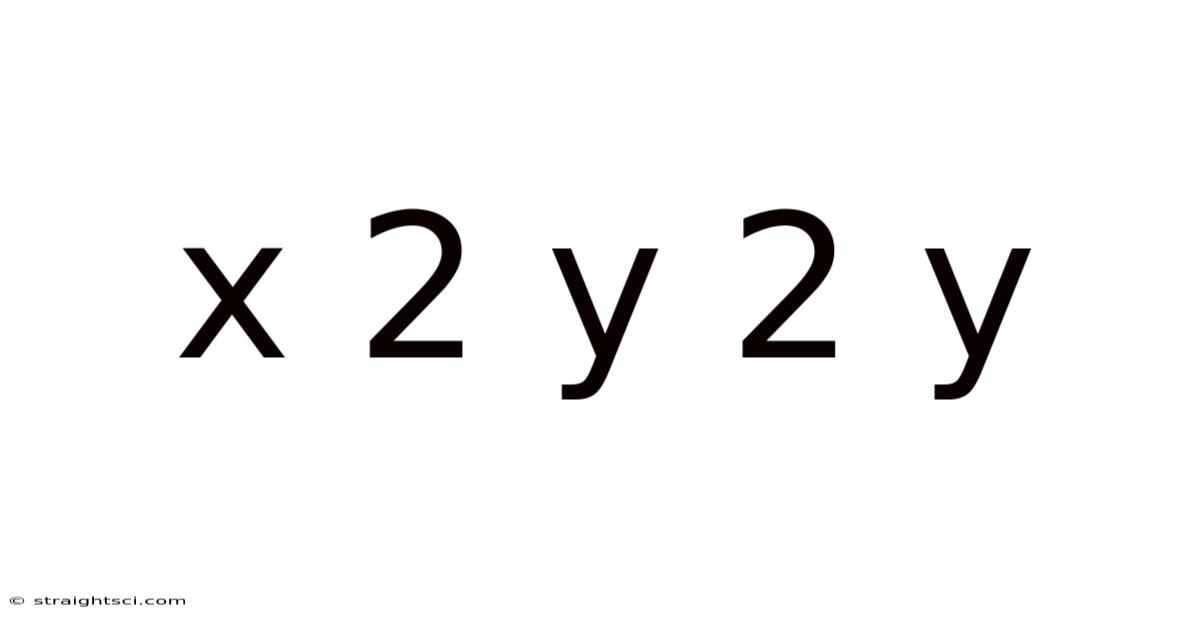
Table of Contents
Understanding and Solving Equations of the Form x² + 2y² = y
This article delves into the mathematical exploration of equations in the form x² + 2y² = y. We'll dissect its structure, explore methods for solving it, and delve into the underlying mathematical concepts. This equation, while seemingly simple, presents interesting challenges and opportunities for understanding quadratic equations and their solutions. We'll cover various approaches, suitable for different mathematical backgrounds, ensuring a comprehensive understanding for all readers.
Introduction: Deconstructing the Equation
The equation x² + 2y² = y presents a unique challenge due to the interplay between the x and y variables. Unlike a typical quadratic equation where we solve directly for a single variable, this equation requires a more nuanced approach. Our objective is to find solutions (x, y) that satisfy this equation. We'll examine both analytical methods and consider the graphical representation to gain a deeper understanding of the solution space.
The equation isn't immediately solvable for either x or y in a straightforward manner. The presence of both x² and y² terms, along with a linear y term, suggests a quadratic relationship with potentially multiple solutions or no solutions at all, depending on the values of the variables. We'll explore how to address these complexities.
Method 1: Rearranging and Solving for x
One approach involves rearranging the equation to solve for x in terms of y:
x² = y - 2y²
This allows us to express x as a function of y:
x = ±√(y - 2y²)
This solution highlights a critical point: the expression inside the square root (y - 2y²) must be non-negative for real solutions to exist. Therefore, we have the constraint:
y - 2y² ≥ 0
This inequality can be factored and solved:
y(1 - 2y) ≥ 0
This inequality holds true when 0 ≤ y ≤ 1/2. This means that for real solutions of x, the value of y is restricted to the interval [0, 1/2]. For any y outside this interval, the equation yields imaginary solutions for x.
For every value of y within the interval [0, 1/2], we obtain two values of x (except at the endpoints where x=0). This implies that the solution set is a curve, symmetric about the y-axis.
Method 2: Completing the Square (for y)
Another powerful technique is to complete the square with respect to the variable y. We rewrite the equation as:
x² + 2(y² - y/2) = 0
To complete the square for the y terms, we add and subtract (1/2)² * 2 = 1/8 inside the parenthesis:
x² + 2(y² - y/2 + 1/16 - 1/16) = 0
This simplifies to:
x² + 2((y - 1/4)² - 1/16) = 0
Rearranging the equation:
x² + 2(y - 1/4)² = 1/8
This equation represents an ellipse centered at (0, 1/4) with semi-major axis a = √(1/8) and semi-minor axis b = √(1/16) = 1/4. This provides a geometric interpretation of the solution set. The ellipse's shape and position confirm the restriction on y found in Method 1.
Method 3: Implicit Differentiation (for Advanced Analysis)
For a more advanced approach, we can employ implicit differentiation to analyze the slope of the curve defined by the equation. Differentiating both sides with respect to x, we get:
2x + 4y(dy/dx) = dy/dx
Solving for dy/dx:
dy/dx = 2x / (1 - 4y)
This equation gives the slope of the tangent line at any point (x, y) on the curve. Points where dy/dx is undefined (1 - 4y = 0 or y = 1/4) correspond to vertical tangents. The analysis of the first derivative helps understand the curve's behavior and locate potential maxima, minima, or points of inflection. Further analysis using the second derivative would provide more detailed information about concavity.
Graphical Representation
Plotting the equation x² + 2y² = y reveals an ellipse-like curve confined within the boundaries 0 ≤ y ≤ 1/2. This visual representation confirms the analytical results obtained through the different methods. The symmetry about the y-axis is evident, and the limitations on the range of y values become immediately clear. Software such as graphing calculators or mathematical software packages can easily generate the graph, providing a valuable tool for understanding the solution space.
Frequently Asked Questions (FAQ)
-
Q: Are there any integer solutions to the equation?
A: By inspecting the equation and the solution constraints (0 ≤ y ≤ 1/2), it’s evident that there are no integer solutions. The only possible integer value for y is 0, which results in x = 0. All other solutions involve non-integer values for both x and y.
-
Q: What happens if the equation is modified, say, to x² + 2y² = 2y?
A: This modification changes the solution set significantly. Similar techniques, like completing the square or rearranging and solving for x, can be applied, but the resulting curve and solution constraints will differ. The resulting curve will be a scaled and potentially shifted version of the original.
-
Q: Can this equation be solved using numerical methods?
A: Yes, numerical methods such as the Newton-Raphson method or iterative techniques can be used to find approximate solutions for x and y, especially if analytical solutions are difficult to obtain for modified versions of the equation.
-
Q: What is the significance of the constraint 0 ≤ y ≤ 1/2?
A: This constraint arises from the requirement that the expression under the square root (y - 2y²) must be non-negative for real solutions of x. It defines the boundaries within which the curve exists and highlights that the equation has no real solutions for y values outside this interval.
Conclusion: A Comprehensive Exploration
The equation x² + 2y² = y, though seemingly simple, presents a rich opportunity to explore various mathematical concepts and techniques. We've explored several methods—rearranging and solving for x, completing the square, and implicit differentiation—demonstrating the versatility of mathematical approaches. The graphical representation further solidified our understanding, visually confirming the limitations on y and the elliptical nature of the solution set. By combining analytical and graphical methods, we achieved a complete understanding of the solution space and the underlying mathematical principles governing this intriguing equation. This exploration emphasizes the importance of combining different mathematical tools to achieve a thorough understanding of even seemingly simple equations. The techniques and insights gained here are applicable to a wider range of quadratic equations and related problems, reinforcing the value of this detailed analysis.
Latest Posts
Latest Posts
-
Target Profit Pricing Refers To
Sep 02, 2025
-
X 2 Y 2 3
Sep 02, 2025
-
Quarter Acre To Square Feet
Sep 02, 2025
-
Convert 6 Cm To Inches
Sep 02, 2025
-
Difference Between Prism And Pyramid
Sep 02, 2025
Related Post
Thank you for visiting our website which covers about X 2 Y 2 Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.