X 2 Y 2 3
straightsci
Sep 02, 2025 · 6 min read
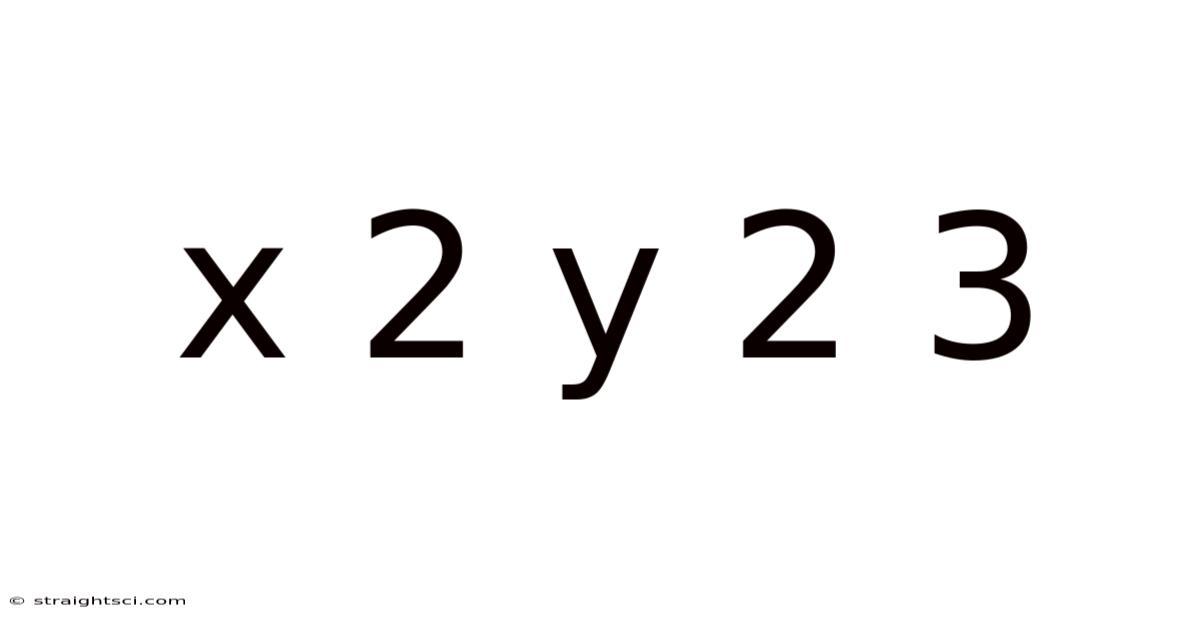
Table of Contents
Decoding the Enigma: A Deep Dive into x² + y² = 3
The equation x² + y² = 3 might seem deceptively simple at first glance. It's a Diophantine equation, meaning we're looking for integer solutions – whole numbers that satisfy the equation. However, the seemingly straightforward nature of this equation belies a rich mathematical landscape, touching upon concepts in number theory, geometry, and even abstract algebra. This article will delve into the intricacies of solving x² + y² = 3, exploring its solutions, the underlying mathematical principles, and related concepts to provide a comprehensive understanding.
Introduction: Understanding the Equation
At its core, x² + y² = 3 represents a circle with a radius of √3 in the Cartesian coordinate system. We are searching for points (x, y) where both x and y are integers and lie on this circle. This seemingly simple geometric interpretation immediately hints at the potential scarcity of solutions. The irrationality of √3 plays a crucial role in determining the feasibility of integer solutions. Unlike the equation x² + y² = 4, which has several integer solutions (e.g., (2,0), (0,2), (-2,0), (0,-2)), the specific value of 3 introduces significant constraints.
Searching for Integer Solutions
Let's embark on a systematic search for integer solutions. We can approach this problem using brute force – testing various integer values for x and y. However, this method is inefficient and doesn't offer much insight into the underlying mathematical structure.
- Testing Small Values: If we let x = 0, we get y² = 3, which has no integer solution for y. Similarly, if y = 0, we have x² = 3, again yielding no integer solution.
- Considering Positive and Negative Values: Since x² and y² are always non-negative, we can restrict our search to non-negative integers without loss of generality. The negative counterparts will automatically be solutions as well.
- Exploring Larger Numbers: As we test larger integer values for x and y, we will quickly observe that the sum x² + y² consistently falls short of or exceeds 3.
This exhaustive search reveals a crucial fact: there are no integer solutions to the equation x² + y² = 3.
The Mathematical Proof: Why No Integer Solutions Exist
The lack of integer solutions isn't a matter of chance; it's a consequence of deep mathematical properties. We can provide a rigorous proof based on modular arithmetic and the properties of quadratic residues.
Proof by Contradiction:
Let's assume there exists an integer solution (x, y) such that x² + y² = 3.
-
Modulo 4 Analysis: Consider the equation modulo 4 (i.e., examining the remainders when divided by 4). The quadratic residues modulo 4 are 0 and 1. This means that any perfect square (x² or y²) can only leave a remainder of 0 or 1 when divided by 4.
-
Possible Combinations: Let's analyze the possible combinations of remainders for x² and y²:
- If x² ≡ 0 (mod 4) and y² ≡ 0 (mod 4), then x² + y² ≡ 0 (mod 4).
- If x² ≡ 0 (mod 4) and y² ≡ 1 (mod 4), then x² + y² ≡ 1 (mod 4).
- If x² ≡ 1 (mod 4) and y² ≡ 0 (mod 4), then x² + y² ≡ 1 (mod 4).
- If x² ≡ 1 (mod 4) and y² ≡ 1 (mod 4), then x² + y² ≡ 2 (mod 4).
-
Contradiction: The equation x² + y² = 3 implies that x² + y² ≡ 3 (mod 4). However, none of the possible combinations of remainders for x² and y² result in a remainder of 3 when added together. This contradiction proves that our initial assumption – the existence of an integer solution – must be false. Therefore, there are no integer solutions to the equation x² + y² = 3.
Extending the Concept: Variations and Related Equations
The analysis of x² + y² = 3 provides a foundation for understanding similar Diophantine equations. Let's explore some related concepts:
-
Different Right-Hand Sides: Changing the right-hand side of the equation drastically alters the solution set. For example, x² + y² = 4 has several integer solutions, while x² + y² = 5 also has solutions. The analysis of these equations often involves similar techniques, including modular arithmetic and considerations of quadratic residues.
-
Higher Dimensions: The concept can be extended to higher dimensions. For instance, we could consider equations like x² + y² + z² = n, where we search for integer solutions in three-dimensional space. The complexity increases with the number of variables and the value of n.
-
Sums of Squares Theorem: A fundamental theorem in number theory states that a positive integer can be written as a sum of two squares if and only if each prime factor of the form 4k+3 appears with an even exponent in its prime factorization. This theorem provides a powerful tool for analyzing the solvability of equations of the form x² + y² = n.
-
Applications in Geometry: The equation x² + y² = r², where r is the radius, represents a circle. Finding integer solutions corresponds to finding points on the circle with integer coordinates. This has implications in various geometric problems and constructions.
Frequently Asked Questions (FAQ)
-
Q: Are there any real solutions to x² + y² = 3?
- A: Yes, there are infinitely many real solutions. These solutions form a circle with a radius of √3 in the Cartesian plane.
-
Q: What about rational solutions?
- A: While there are no integer solutions, there are infinitely many rational solutions. These can be found using techniques from number theory and algebraic geometry.
-
Q: How does this relate to other areas of mathematics?
- A: This equation connects to various fields, including number theory (specifically, Diophantine equations and quadratic residues), geometry (circles and coordinate systems), and abstract algebra (rings and fields).
-
Q: Is there a general method to solve all Diophantine equations?
- A: No, there is no general algorithm to solve all Diophantine equations. The solvability and difficulty of solving them depend heavily on the specific form of the equation. Many are incredibly challenging and remain unsolved.
Conclusion: The Significance of Simplicity
The seemingly simple equation x² + y² = 3 has unveiled a surprising depth of mathematical concepts. The absence of integer solutions, far from being trivial, highlights the subtleties and intricacies of number theory. Through exploring this equation, we've touched upon crucial tools like modular arithmetic, the nature of quadratic residues, and the broader landscape of Diophantine equations. Understanding the intricacies of this equation serves as a gateway to appreciating the power and elegance of mathematical reasoning, demonstrating that even seemingly simple problems can lead to profound insights. The journey of exploring this equation underscores the beauty of mathematics: the unexpected connections, the rigorous proofs, and the endless possibilities for exploration. Further investigations into similar equations, coupled with the tools we've discussed, can open up fascinating new avenues of mathematical discovery.
Latest Posts
Latest Posts
-
Slope And Tangent Line Calculator
Sep 02, 2025
-
Absolute And Relative Refractory Period
Sep 02, 2025
-
16 Ounces Converted Into Grams
Sep 02, 2025
-
Scientific Notation Speed Of Light
Sep 02, 2025
-
What Is A Hanging Chad
Sep 02, 2025
Related Post
Thank you for visiting our website which covers about X 2 Y 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.