X 2 Y 2 X
straightsci
Sep 14, 2025 · 6 min read
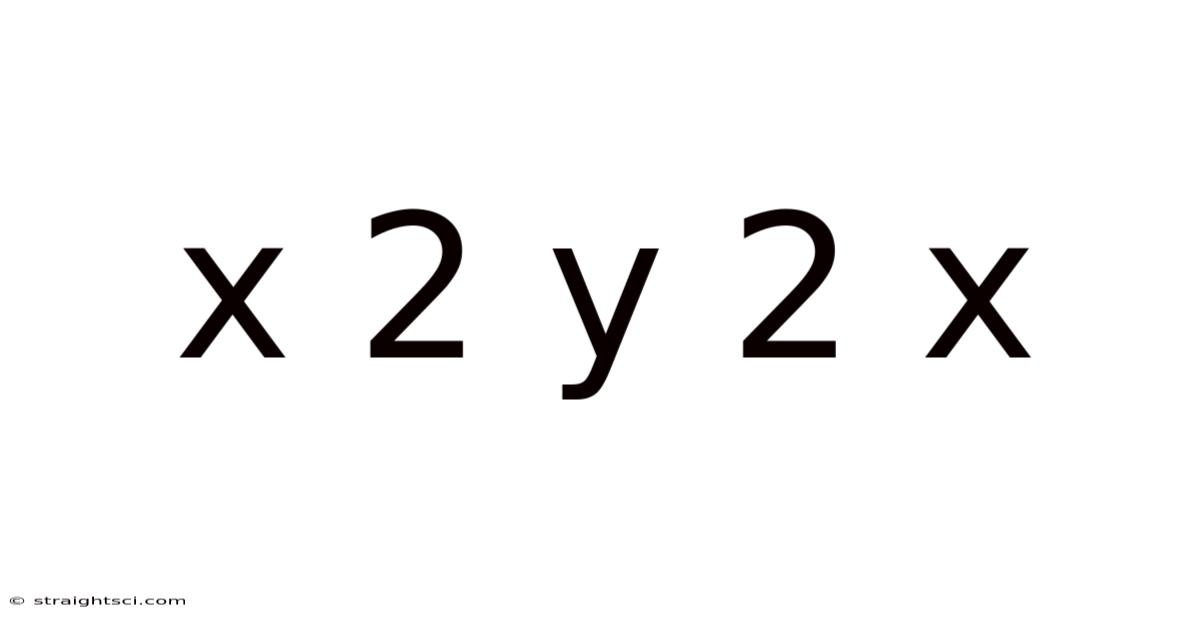
Table of Contents
Decoding the Mystery: A Deep Dive into x²y²x
The expression "x²y²x" might seem simple at first glance, but it opens a door to a fascinating world of mathematical concepts and interpretations. This seemingly straightforward algebraic expression offers opportunities to explore various mathematical fields, including algebra, calculus, and even abstract algebra depending on the context. This article will delve into the multiple meanings and interpretations of x²y²x, examining its basic algebraic structure, potential interpretations in different mathematical contexts, and exploring related concepts to offer a comprehensive understanding.
Understanding the Fundamentals: Basic Algebraic Interpretation
At its most basic level, x²y²x represents a term in an algebraic expression. Let's break down the components:
- x²: This signifies 'x' multiplied by itself (x * x). It's a term involving the variable 'x' raised to the power of 2, commonly known as 'x squared'.
- y²: Similarly, this represents 'y' multiplied by itself (y * y), or 'y squared'.
- x: This is simply the variable 'x'.
Therefore, the entire expression, x²y²x, can be rewritten as (x * x) * (y * y) * x. This represents the product of three terms: x squared, y squared, and x. The order of multiplication doesn't change the result due to the commutative property of multiplication. This means that x²y²x = x³y². This simplification reveals that the expression is essentially a monomial – a single term comprising variables and constants.
Expanding the Horizons: Interpretations Beyond Basic Algebra
While the basic algebraic interpretation provides a foundation, the expression x²y²x can take on richer meanings depending on the context.
1. Context in Polynomial Algebra:
In the realm of polynomial algebra, x²y²x is simply a term within a larger polynomial expression. For instance, it could be part of a polynomial like:
3x³y² + 2x²y²x - 5xy + 7
In this case, understanding the order of operations and simplifying the expression (as shown above to x³y²) is crucial for further algebraic manipulations, such as combining like terms or factoring the polynomial.
2. Exploring the Context of Calculus:
If x and y are considered variables representing functions of a single variable (say, 't'), then x²y²x becomes a composite function. Imagine x = f(t) and y = g(t). Then, x²y²x translates to [f(t)]²[g(t)]²f(t), which is a function of 't'. This opens doors to performing calculus operations such as finding derivatives or integrals. For example, if we had specific functions for x and y, we could calculate the derivative with respect to 't' using the chain rule and product rule.
Let's consider a simple example:
Let x = t and y = t². Then x²y²x becomes (t)²(t²)²(t) = t⁷. The derivative with respect to 't' would be a straightforward 7t⁶. However, with more complex functions for x and y, the process becomes significantly more involved.
3. Abstract Algebra and Group Theory:
In abstract algebra, the expression could represent elements within a group. If 'x' and 'y' represent elements within a group under a defined operation (such as multiplication), then x²y²x represents the result of applying the group's operation sequentially. The outcome depends heavily on the specific group's properties (commutative, associative, etc.). For instance, if the group is non-commutative, the order of operations is critical. x²y²x would not necessarily be equal to x³y². The result could be drastically different depending on the group's operation table.
4. Geometric Interpretations:
While less direct, the expression can have indirect geometric interpretations. For example, if 'x' and 'y' represent coordinates in a 2D or 3D space (depending on the context), then x² and y² could represent squares of distances from the origin along the x and y axes respectively. However, a direct geometric interpretation of the entire expression x²y²x is not immediately apparent without further context or definitions.
Beyond the Expression: Related Mathematical Concepts
Understanding x²y²x opens doors to various related mathematical concepts:
- Exponents and Powers: The expression fundamentally relies on the concept of exponents and powers, explaining how repeated multiplication is represented concisely.
- Variables and Constants: The 'x' and 'y' terms highlight the use of variables to represent unknown or changing quantities.
- Monomials, Polynomials, and Algebraic Expressions: The expression itself is a monomial, forming the building block of larger polynomial expressions.
- Order of Operations (PEMDAS/BODMAS): The order of operations dictates the sequence of calculations within the expression.
- Commutative and Associative Properties: These properties govern the rearrangement and grouping of terms in multiplication.
- Functions and Composition of Functions (in Calculus): The expression can represent a composite function in a calculus setting.
- Group Theory and Abstract Algebra: In abstract algebra, the expression can represent group operations.
Frequently Asked Questions (FAQ)
Q1: Can x²y²x be simplified further?
A1: Yes, using the commutative property of multiplication, it simplifies to x³y².
Q2: What if x and y were numbers?
A2: If x and y were assigned numerical values, the expression becomes a simple arithmetic calculation. For example, if x = 2 and y = 3, then x²y²x = (2²)(3²)(2) = 4 * 9 * 2 = 72.
Q3: What are the limitations of simplifying x²y²x to x³y²?
A3: The simplification only holds true under the standard rules of arithmetic and algebra. It does not apply in all mathematical contexts, particularly in abstract algebra where the commutative property might not hold.
Q4: How does the context affect the interpretation of x²y²x?
A4: The interpretation depends heavily on the context. In basic algebra, it's a simple algebraic term. In calculus, it can represent a composite function. In abstract algebra, it might represent group operations.
Conclusion: A Versatile Expression with Deep Implications
The simple algebraic expression x²y²x, while appearing straightforward, reveals the multifaceted nature of mathematics. Its interpretation can range from a basic algebraic term to a complex function or an abstract algebraic element depending on the surrounding context. Understanding this expression provides a strong foundation for exploring various mathematical concepts, highlighting the importance of context in mathematical interpretation and problem-solving. The exploration of x²y²x serves as a microcosm of the wider mathematical landscape, demonstrating how a seemingly simple concept can lead to deeper and more nuanced understandings. Its versatility highlights the power of mathematical notation and the importance of contextual awareness in navigating the diverse applications of mathematical principles. This comprehensive exploration offers a deeper understanding not only of the expression itself but also of the fundamental building blocks that underpin higher mathematical concepts.
Latest Posts
Latest Posts
-
Derivative Of X 2 3
Sep 15, 2025
-
How Do I Spell Professional
Sep 15, 2025
-
50 Kg Converted To Pounds
Sep 15, 2025
-
What Does In Succession Mean
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 2 Y 2 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.