Derivative Of X 2 3
straightsci
Sep 15, 2025 · 6 min read
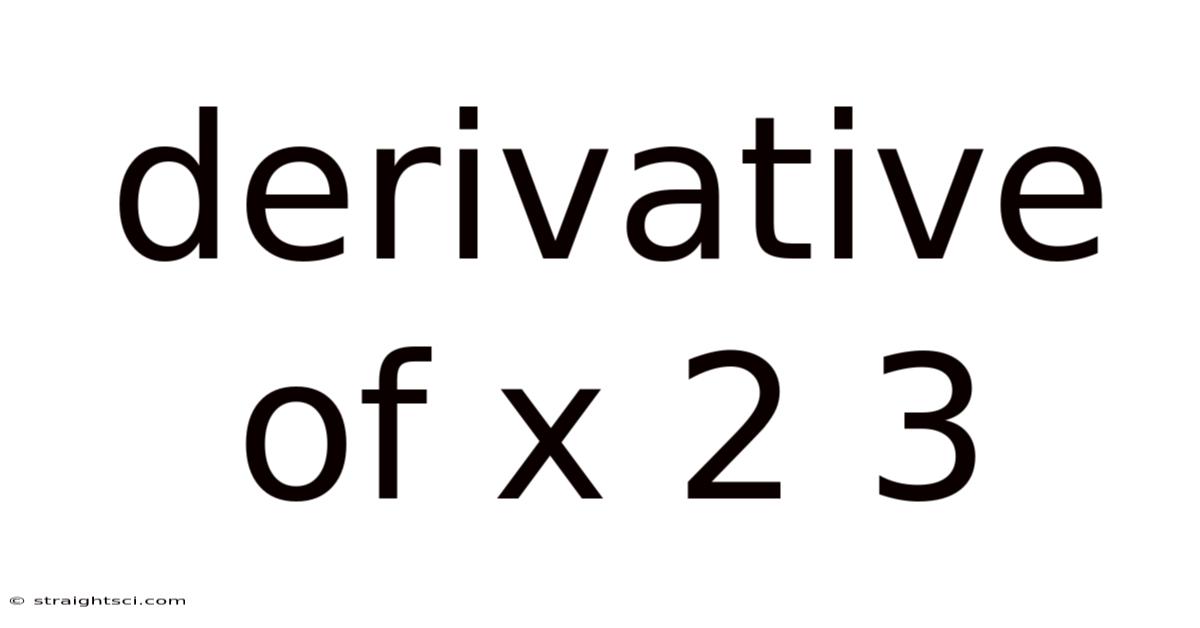
Table of Contents
Understanding the Derivative of x<sup>2/3</sup>: A Comprehensive Guide
Finding the derivative of a function is a fundamental concept in calculus. This article will delve into the process of finding the derivative of x<sup>2/3</sup>, explaining the underlying principles and providing a step-by-step guide accessible to those with varying levels of mathematical background. We'll cover the power rule, its application to fractional exponents, and address common questions and potential pitfalls. This comprehensive guide will equip you with a solid understanding of this important calculus concept.
Introduction: The Power Rule and Fractional Exponents
The cornerstone of finding the derivative of x<sup>2/3</sup> is the power rule of differentiation. The power rule states that the derivative of x<sup>n</sup>, where 'n' is any real number, is nx<sup>n-1</sup>. This seemingly simple rule unlocks the ability to differentiate a vast array of functions.
However, the power rule's elegance extends even to fractional exponents like the 2/3 in our target function. Fractional exponents represent roots and powers simultaneously. For example, x<sup>2/3</sup> is equivalent to (x<sup>2</sup>)<sup>1/3</sup>, or the cube root of x squared, or equivalently (x<sup>1/3</sup>)<sup>2</sup>, the square of the cube root of x. This dual representation helps visualize the function's behavior.
Step-by-Step Differentiation of x<sup>2/3</sup> using the Power Rule
Let's apply the power rule directly to find the derivative of f(x) = x<sup>2/3</sup>.
-
Identify the exponent: In our function, f(x) = x<sup>2/3</sup>, the exponent 'n' is 2/3.
-
Apply the power rule: According to the power rule, the derivative f'(x) is obtained by multiplying the function by the exponent and then reducing the exponent by 1. Therefore:
f'(x) = (2/3)x<sup>(2/3) - 1</sup>
-
Simplify the exponent: Subtracting 1 from 2/3 gives us:
(2/3) - 1 = (2/3) - (3/3) = -1/3
-
Write the final derivative: Substituting the simplified exponent back into the equation, we get:
f'(x) = (2/3)x<sup>-1/3</sup>
-
Express in radical form (optional): While the derivative is perfectly valid in exponential form, it can also be expressed using radicals for better understanding:
f'(x) = 2 / (3x<sup>1/3</sup>) or f'(x) = 2 / (3∛x)
This final expression, f'(x) = 2 / (3∛x), represents the derivative of x<sup>2/3</sup>. It tells us the instantaneous rate of change of the function at any given point x. Notice that the derivative is undefined at x = 0, reflecting a vertical tangent to the original function at that point.
Explanation of the Derivative's Behavior
The derivative, f'(x) = 2 / (3∛x), provides crucial insights into the original function's behavior.
-
Positive values of x: For positive values of x, the derivative is positive, indicating that the original function f(x) = x<sup>2/3</sup> is increasing. As x increases, the rate of increase slows down, reflecting the curve of the function flattening out.
-
Negative values of x: For negative values of x, the derivative is negative, indicating that the function is decreasing. Similar to the positive x values, the rate of decrease slows down as |x| increases.
-
Undefined at x = 0: The derivative is undefined at x = 0 because the cube root of 0 is 0, resulting in division by zero. This reflects the fact that the function f(x) = x<sup>2/3</sup> has a cusp (a sharp point) at x = 0. The tangent line is vertical at this point.
Graphical Representation
Visualizing the function f(x) = x<sup>2/3</sup> and its derivative f'(x) = 2 / (3∛x) graphically further reinforces the understanding of their relationship. The graph of f(x) shows a smooth curve passing through the origin with a cusp at (0,0). The graph of f'(x) displays a hyperbola-like shape, reflecting the undefined value at x=0 and showing positive values for positive x and negative values for negative x. The steepness of the curve in the graph of f(x) corresponds to the magnitude of f'(x). The flatter the curve, the closer f'(x) is to zero.
Further Applications and Extensions
The principles illustrated here extend far beyond the simple function x<sup>2/3</sup>. The power rule remains a fundamental tool for differentiating numerous polynomial and other functions involving fractional and negative exponents. Understanding the derivative of x<sup>2/3</sup> provides a stepping stone to tackling more complex derivatives involving combinations of functions, chain rule, product rule, and quotient rule. These advanced techniques build upon the basic understanding of the power rule.
Frequently Asked Questions (FAQ)
Q1: What is the difference between x<sup>2/3</sup> and x<sup>3/2</sup>?
A1: The key difference lies in the order of operations. x<sup>2/3</sup> represents the cube root of x squared ((x²)<sup>1/3</sup> or (x<sup>1/3</sup>)²), whereas x<sup>3/2</sup> represents the square of the cube root of x ( (x<sup>1/3</sup>)³). Their derivatives are also different: the derivative of x<sup>3/2</sup> is (3/2)x<sup>1/2</sup>.
Q2: Can the power rule be applied to all functions?
A2: No, the power rule specifically applies to functions of the form x<sup>n</sup>, where n is a real number. For other functions (e.g., trigonometric functions, exponential functions, logarithmic functions), different differentiation rules are required.
Q3: What does it mean when the derivative is undefined at a point?
A3: An undefined derivative at a specific point usually indicates a discontinuity or a sharp change in the function's slope at that point. This could be a cusp, a vertical tangent, or a point of non-differentiability.
Q4: Why is it important to understand derivatives?
A4: Derivatives are crucial in various fields like physics (velocity and acceleration), engineering (optimization problems), economics (marginal cost and revenue), and computer science (machine learning algorithms). They provide a mathematical framework to analyze rates of change and optimize processes.
Q5: How can I practice finding derivatives?
A5: The best way to improve your understanding and proficiency in differentiation is through consistent practice. Start with simple functions and gradually work your way up to more complex ones. Use online resources, textbooks, and practice problems to strengthen your skills.
Conclusion
The process of finding the derivative of x<sup>2/3</sup>, while seemingly straightforward, illustrates a fundamental concept in calculus – the power rule and its application to fractional exponents. Understanding this concept unlocks the door to a deeper appreciation of calculus and its diverse applications. Remember, mastering calculus requires practice and patience. By understanding the underlying principles and applying the steps outlined, you can confidently approach and solve a wide range of differentiation problems. The ability to find the derivative of functions like x<sup>2/3</sup> forms a crucial building block for tackling more complex calculus problems. This knowledge will serve you well in various mathematical and scientific pursuits.
Latest Posts
Latest Posts
-
Hydrogen Peroxide And Manganese Oxide
Sep 15, 2025
-
Factor 2x 2 5x 3
Sep 15, 2025
-
2 5 Kg To Lbs
Sep 15, 2025
-
D Vit 1 2at 2
Sep 15, 2025
-
Challenge The Status Quo Definition
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of X 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.