Whats 5 Percent Of 2000
straightsci
Sep 12, 2025 · 6 min read
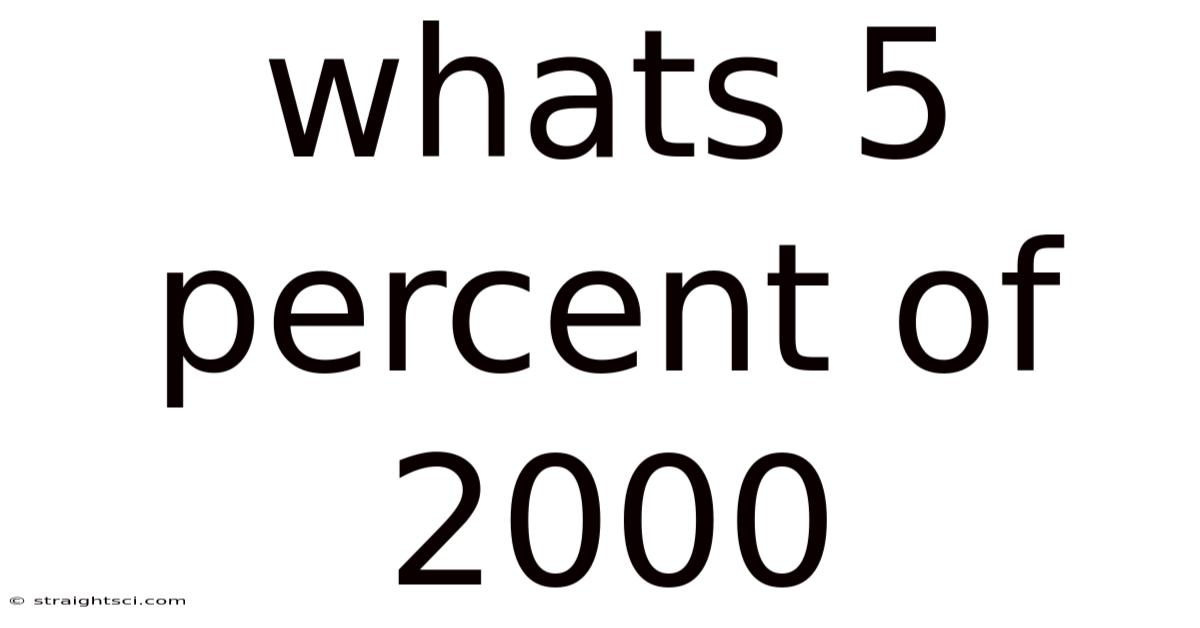
Table of Contents
What's 5 Percent of 2000? A Comprehensive Guide to Percentages and Their Applications
Finding 5 percent of 2000 might seem like a simple arithmetic problem, but understanding the underlying concepts of percentages is crucial for a wide range of applications in everyday life, from calculating discounts and taxes to understanding financial statements and statistical data. This article will not only answer the question "What's 5 percent of 2000?" but also delve into the methods for calculating percentages, explore real-world applications, and address frequently asked questions.
Introduction: Understanding Percentages
Percentages are a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 5% literally means 5 out of every 100. Calculating percentages involves understanding the relationship between the percentage, the whole amount, and the resulting part. In our case, we want to find 5% of 2000, where 2000 represents the whole amount.
Methods for Calculating 5% of 2000
There are several ways to calculate 5% of 2000. We'll explore three common approaches:
-
Using the Decimal Equivalent:
The most straightforward method involves converting the percentage to its decimal equivalent. To do this, divide the percentage by 100. So, 5% becomes 5/100 = 0.05. Then, multiply this decimal by the whole amount:
0.05 * 2000 = 100
Therefore, 5% of 2000 is 100.
-
Using Fractions:
Percentages can also be expressed as fractions. 5% is equivalent to the fraction 5/100, which simplifies to 1/20. To find 5% of 2000, multiply the fraction by the whole amount:
(1/20) * 2000 = 100
Again, we arrive at the answer: 100.
-
Using Proportions:
A proportion sets up an equivalence between two ratios. We can set up a proportion to solve for 5% of 2000:
5/100 = x/2000
To solve for x (5% of 2000), cross-multiply:
100x = 5 * 2000 100x = 10000 x = 10000/100 x = 100
This method reinforces the concept of percentages as a ratio and provides a systematic approach to solving percentage problems.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world situations. Here are some examples:
-
Sales and Discounts: Stores frequently offer discounts expressed as percentages. For example, a 20% discount on a $50 item means you'll save 20% of $50, which is $10, making the final price $40. This same principle applies to calculating sales tax, where a percentage is added to the original price.
-
Financial Calculations: Percentages are fundamental in finance. Interest rates on loans and savings accounts are expressed as percentages. Calculating compound interest, which is interest earned on both the principal amount and accumulated interest, heavily relies on percentage calculations. Understanding percentage changes in investments is crucial for assessing portfolio performance.
-
Statistics and Data Analysis: Percentages are widely used in statistics to represent proportions and probabilities. For instance, a survey might report that 60% of respondents favor a particular policy, indicating that 60 out of every 100 respondents hold that opinion. Percentage changes are used to track trends and analyze data over time.
-
Everyday Budgeting: Understanding percentages helps in budgeting effectively. For example, you can determine what percentage of your income you allocate to various expenses such as housing, food, transportation, and savings. This facilitates better financial planning and helps you stay within your budget.
-
Scientific and Engineering Applications: Percentages are employed in many scientific and engineering fields to express error margins, efficiency rates, and various other proportions.
A Deeper Dive into Percentage Concepts
To further solidify your understanding, let's explore some related percentage concepts:
-
Finding the Percentage: If you know the part and the whole, you can find the percentage by dividing the part by the whole and multiplying by 100. For example, if 150 out of 500 people prefer a certain brand, the percentage is (150/500) * 100 = 30%.
-
Finding the Whole Amount: If you know the part and the percentage, you can find the whole amount by dividing the part by the percentage (expressed as a decimal) and multiplying by 100. For instance, if 25 is 10% of a number, the number is (25/0.1) * 100 = 250.
-
Percentage Increase and Decrease: These calculations are used to determine the change in a value over time. A percentage increase is calculated by dividing the increase by the original value and multiplying by 100. A percentage decrease is calculated similarly, but the difference is subtracted from the original value.
-
Percentage Points: It's crucial to distinguish between percentage points and percentage change. A change from 20% to 25% is a 5 percentage point increase, but a 25% increase from the original 20%.
Advanced Percentage Applications:
While finding 5% of 2000 is a simple calculation, the underlying principles can be applied to more complex scenarios:
-
Compound Interest: Interest that's calculated not only on the principal but also on the accumulated interest, leading to exponential growth over time.
-
Discount Series: Calculating the final price after applying multiple discounts successively. The discounts don't simply add up; each discount is applied to the progressively reduced price.
-
Tax Calculations with Multiple Brackets: Many tax systems have progressive tax brackets. Calculating the total tax owed requires applying different percentage rates to different income levels.
Frequently Asked Questions (FAQs)
-
What is the easiest way to calculate percentages? The easiest way is often using the decimal equivalent method. Convert the percentage to a decimal (divide by 100) and multiply by the whole amount.
-
How can I calculate percentages quickly in my head? For simple percentages like 10%, 25%, or 50%, mental math strategies are possible. For example, 10% is simply moving the decimal point one place to the left. 50% is half the number, and 25% is one-quarter of the number.
-
Are there any online calculators for percentages? Yes, many online calculators are readily available that can perform percentage calculations automatically.
-
Why is understanding percentages important? Understanding percentages is crucial for making informed decisions in various aspects of life, from personal finances to career choices to understanding data analysis.
Conclusion:
We've determined that 5% of 2000 is 100. However, the true value of this exercise lies not just in the answer itself, but in understanding the broader concepts of percentages and their applications. From basic arithmetic to complex financial calculations, the ability to work with percentages is a vital skill that enhances decision-making and problem-solving capabilities in various areas of life. Mastering percentage calculations empowers you to navigate the world of numbers with confidence and effectively interpret numerical information presented in countless everyday scenarios. The seemingly simple question, "What's 5 percent of 2000?" opens the door to a far more extensive understanding of a fundamental mathematical concept.
Latest Posts
Latest Posts
-
Age Of Viability Of Fetus
Sep 13, 2025
-
Square Root Of X 2
Sep 13, 2025
-
Convert 130 Lbs To Kg
Sep 13, 2025
-
Convert 4 0z To Grams
Sep 13, 2025
-
3 Years How Many Months
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Whats 5 Percent Of 2000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.