Square Root Of X 2
straightsci
Sep 13, 2025 · 5 min read
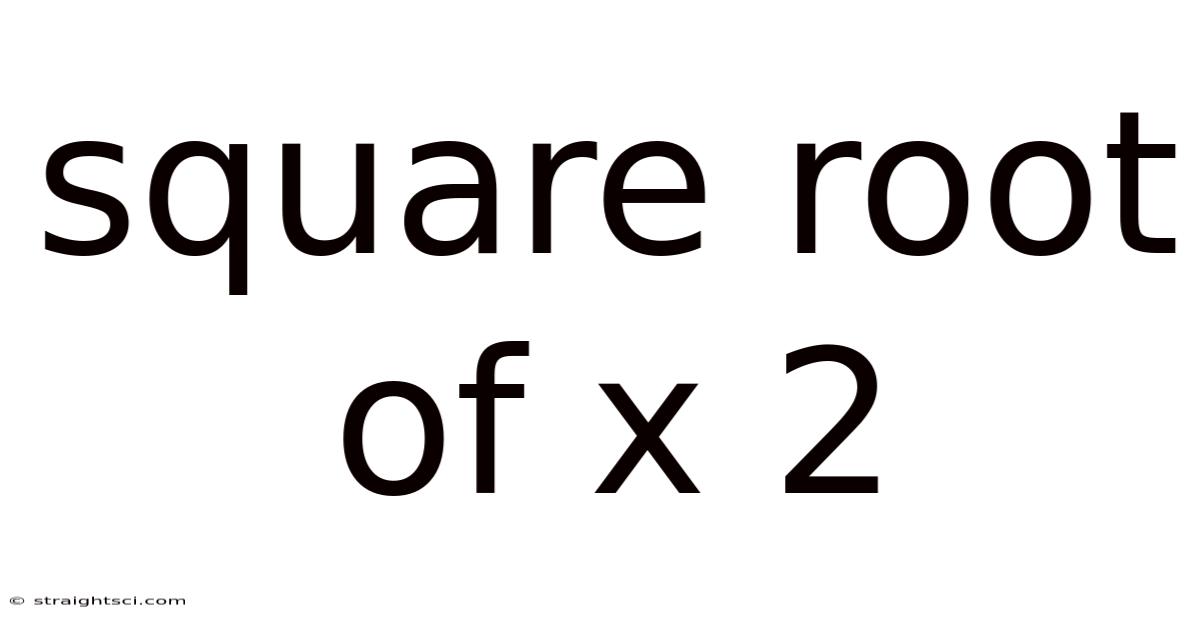
Table of Contents
Understanding the Square Root of x²: A Comprehensive Guide
The square root of x², denoted as √(x²), is a fundamental concept in mathematics with far-reaching applications across various fields. This comprehensive guide will explore this concept in detail, moving from basic understanding to more advanced considerations, ensuring a thorough grasp of its implications. We'll delve into its definition, properties, different approaches to solving it, potential pitfalls, and real-world applications. This article aims to provide a complete understanding of the square root of x², suitable for learners of all levels.
What is the Square Root of x²?
At its core, the square root of a number is a value that, when multiplied by itself, equals the original number. Therefore, the square root of x² is the number that, when multiplied by itself, results in x². This seems straightforward, and in many cases, it is: the answer is simply x. However, there's a crucial nuance that needs careful consideration, particularly when dealing with negative numbers and the broader context of complex numbers.
Understanding Absolute Value and its Significance
The simplified answer, x, is only completely accurate when x is non-negative (x ≥ 0). This is because the square of both a positive and a negative number results in a positive number. For example:
- 3² = 9, and √9 = 3
- (-3)² = 9, and √9 = 3
This leads us to the importance of absolute value. The absolute value of a number is its distance from zero, always represented as a non-negative value. It's denoted by |x|. Therefore, the accurate and complete representation of the square root of x² is:
√(x²) = |x|
This means the square root of x² is always the absolute value of x. This seemingly small detail is crucial for avoiding errors in mathematical calculations and problem-solving.
Solving for the Square Root of x²: Different Approaches
While the conceptual understanding is key, let's explore different approaches to solving for √(x²):
-
Direct Calculation (for non-negative x): If x is non-negative, the square root of x² is simply x. For instance, if x = 4, then √(4²) = √16 = 4.
-
Using Absolute Value (for all real numbers): This is the universally applicable method. Regardless of whether x is positive, negative, or zero, the square root of x² is always the absolute value of x. For example:
- If x = 5, √(5²) = |5| = 5
- If x = -5, √((-5)²) = |-5| = 5
-
Graphical Representation: Visualizing the function y = √(x²) on a graph helps solidify the understanding. The graph will show a V-shaped curve, reflecting the absolute value. The curve is symmetrical about the y-axis, further illustrating that both positive and negative values of x yield the same positive result for √(x²).
-
Using Properties of Exponents: Recall that √(x²) can also be written as (x²)^(1/2). Using exponent rules, this simplifies to x^(2*(1/2)) = x¹. However, this approach, while mathematically correct, doesn't explicitly incorporate the absolute value, so caution is necessary.
Advanced Considerations and Potential Pitfalls
While the core concept is relatively simple, several advanced considerations and potential pitfalls deserve attention:
-
Complex Numbers: The discussion so far has focused on real numbers. When dealing with complex numbers (numbers involving the imaginary unit i, where i² = -1), the concept of square root becomes more nuanced. The square root of a complex number has two possible values.
-
Equations Involving √(x²): When solving equations containing √(x²), it's crucial to remember the absolute value. For instance, solving the equation √(x²) = 5 leads to two solutions: x = 5 and x = -5. Simply dropping the absolute value could lead to an incomplete solution set.
-
Calculus and Derivatives: In calculus, the derivative of √(x²) needs to be handled carefully, requiring the chain rule and consideration of the absolute value function's non-differentiability at x = 0.
-
Numerical Methods: For extremely large or complex values of x, numerical methods might be employed to approximate the square root, again emphasizing the importance of considering the absolute value for accurate results.
Real-World Applications of the Square Root of x²
The seemingly simple concept of √(x²) has significant real-world applications across numerous disciplines:
-
Physics: In physics, calculations involving distance, velocity, and acceleration frequently utilize the square root of squared quantities. For example, calculating the magnitude of a vector involves the square root of the sum of the squares of its components.
-
Engineering: Many engineering calculations, particularly those involving geometry, mechanics, and signal processing, rely heavily on the square root of squared values.
-
Computer Science: Computer graphics and image processing utilize this concept extensively in operations involving distance calculations and transformations.
-
Statistics: In statistics, standard deviation and variance calculations utilize the square root of sums of squares.
Frequently Asked Questions (FAQ)
Q1: Is √(x²) always equal to x?
A1: No, √(x²) is always equal to |x| (the absolute value of x). This ensures a non-negative result, accommodating both positive and negative values of x.
Q2: What is the difference between √(x²) and x?
A2: If x is non-negative, they are equal. However, if x is negative, √(x²) is the positive equivalent of x (its absolute value), while x remains negative.
Q3: How do I solve an equation containing √(x²)?
A3: Remember the absolute value. If √(x²) = a, then x = ±a. Consider both the positive and negative solutions.
Q4: Why is the absolute value important in this context?
A4: The absolute value guarantees a non-negative result, consistent with the definition of the square root as a non-negative value.
Q5: What happens when x is a complex number?
A5: The square root of a complex number has two possible solutions, requiring a different approach than simply taking the absolute value.
Conclusion
The seemingly simple concept of the square root of x² reveals subtle yet crucial nuances when examined closely. Understanding the role of absolute value and its implications is essential for accurate calculations and problem-solving in mathematics, physics, engineering, computer science, and other fields. This comprehensive guide has explored various approaches to calculating √(x²), highlighting potential pitfalls and demonstrating its widespread real-world applications. Mastering this concept solidifies a fundamental building block for advanced mathematical endeavors. Remember, while the simple answer might seem to be "x," the complete and accurate answer, encompassing all possibilities, is always |x|, the absolute value of x.
Latest Posts
Latest Posts
-
Capital Of State Of Florida
Sep 13, 2025
-
One And A Half Inch
Sep 13, 2025
-
Dna Fingerprinting And Dna Profiling
Sep 13, 2025
-
Figuring Out Weight Loss Percentage
Sep 13, 2025
-
Equation Of A Line Formula
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.