What's 1/3 As A Percent
straightsci
Aug 27, 2025 · 5 min read
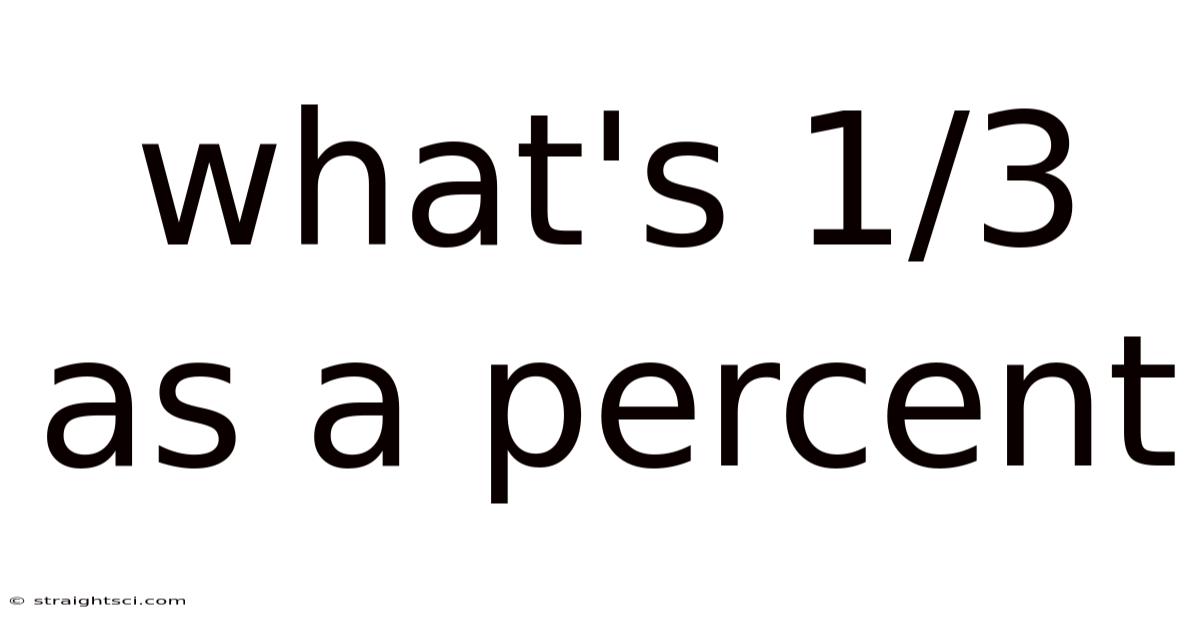
Table of Contents
What's 1/3 as a Percent? A Comprehensive Guide to Fractions, Decimals, and Percentages
Understanding the relationship between fractions, decimals, and percentages is a fundamental skill in mathematics. This comprehensive guide will explore how to convert the fraction 1/3 into a percentage, explaining the process step-by-step and delving into the underlying concepts. We'll also address common misconceptions and explore practical applications of this conversion. By the end, you'll not only know the answer but also understand the 'why' behind the calculation, empowering you to tackle similar conversions with confidence.
Understanding the Basics: Fractions, Decimals, and Percentages
Before diving into the conversion of 1/3 to a percentage, let's establish a solid foundation by defining these three mathematical representations:
-
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, in the fraction 1/3, 1 is the numerator and 3 is the denominator. The denominator indicates how many equal parts the whole is divided into, and the numerator shows how many of those parts are being considered.
-
Decimals: A decimal is another way to represent a part of a whole. It uses a base-ten system, with a decimal point separating the whole number part from the fractional part. For example, 0.5 represents one-half (1/2). Each position to the right of the decimal point represents a decreasing power of ten (tenths, hundredths, thousandths, and so on).
-
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" signifies "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to 1/2 or 0.5.
Converting 1/3 to a Decimal
The first step in converting 1/3 to a percentage is to convert it to a decimal. This is done by dividing the numerator (1) by the denominator (3):
1 ÷ 3 = 0.333333...
Notice that the result is a repeating decimal. The digit 3 repeats infinitely. This is a characteristic of some fractions, and it means the decimal representation is non-terminating. We often round these repeating decimals to a certain number of decimal places for practical purposes. For example, we might round 0.333333... to 0.33 or 0.333 depending on the required level of precision.
Converting the Decimal to a Percentage
Now that we have the decimal representation (approximately 0.3333), we can convert it to a percentage by multiplying by 100 and adding the "%" symbol:
0.3333 × 100 = 33.33%
Therefore, 1/3 is approximately equal to 33.33%. The three dots (...) after 33.33% indicate that this is an approximation, and the actual percentage is a non-terminating decimal.
The Significance of the Repeating Decimal
The repeating decimal in the conversion of 1/3 to a percentage highlights an important aspect of representing fractions as decimals and percentages. Not all fractions can be expressed as terminating decimals. Fractions with denominators that are not factors of powers of 10 (e.g., 2, 5, 10, 20, 50, 100, etc.) will often result in repeating decimals. This is because the decimal system is based on powers of 10.
For 1/3, the denominator (3) is not a factor of any power of 10. This leads to the repeating decimal 0.3333..., which represents the infinitely repeating sequence of 3s.
Different Levels of Accuracy in the Approximation
The accuracy of the percentage representation of 1/3 depends on the number of decimal places we use in our approximation.
- Rounding to one decimal place: 33.3%
- Rounding to two decimal places: 33.33%
- Rounding to three decimal places: 33.333%
While using more decimal places gives a more accurate representation, for most practical purposes, rounding to two decimal places (33.33%) is sufficient. The level of precision required will depend on the specific application.
Practical Applications
Understanding the conversion of 1/3 to a percentage has practical applications in various fields:
-
Finance: Calculating discounts, interest rates, or profit margins. For example, if a store offers a 1/3 discount, it's equivalent to a 33.33% discount.
-
Science: Expressing experimental results or data analysis. For example, if 1/3 of a sample shows a certain characteristic, this can be represented as 33.33%.
-
Everyday life: Sharing or dividing resources equally among three people. Each person would receive approximately 33.33% of the total.
Common Misconceptions
A common misconception is that 1/3 is equal to 33%. While 33% is a close approximation, it's not perfectly accurate. The exact value is 33.333...% (a repeating decimal). The difference, though seemingly small, becomes significant in calculations involving large numbers.
Frequently Asked Questions (FAQ)
Q: Is there a way to express 1/3 as a percentage without using a repeating decimal?
A: No, there isn't. The fraction 1/3 inherently leads to a repeating decimal (0.333...) when converted. The only way to represent it precisely is as the fraction itself or using a notation indicating the repeating decimal (e.g., 0.3̅).
Q: Why is it important to understand this conversion?
A: Understanding the conversion between fractions, decimals, and percentages is essential for various mathematical and practical applications. It allows for flexible representation and manipulation of data, facilitating calculations and interpretations across different contexts.
Q: Can I use a calculator to convert 1/3 to a percentage?
A: Yes, most calculators can perform this conversion. Simply divide 1 by 3 and then multiply the result by 100. However, be aware that the calculator may round the result, so you might see a slightly different value depending on the calculator's settings.
Q: How accurate does the percentage representation need to be?
A: The required accuracy depends on the context. For many everyday purposes, rounding to two decimal places (33.33%) is perfectly sufficient. However, in scientific or financial applications where high precision is crucial, more decimal places might be necessary.
Conclusion
Converting 1/3 to a percentage involves understanding the relationships between fractions, decimals, and percentages. While the exact value is 33.333...% (a repeating decimal), for most applications, approximating it to 33.33% is sufficiently accurate. Grasping this fundamental concept expands your mathematical skills and provides the tools to tackle similar conversions with confidence, empowering you to confidently interpret and apply mathematical concepts in diverse situations. Remember to always consider the context and the required level of accuracy when working with fractions, decimals, and percentages.
Latest Posts
Latest Posts
-
Minimum Value Of A Parabola
Aug 27, 2025
-
Y 2 X 1 2
Aug 27, 2025
-
Pros Of A Market Economy
Aug 27, 2025
-
Where Is A Cytoplasm Found
Aug 27, 2025
-
Is A Rabbit A Herbivore
Aug 27, 2025
Related Post
Thank you for visiting our website which covers about What's 1/3 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.