Y 2 X 1 2
straightsci
Aug 27, 2025 · 5 min read
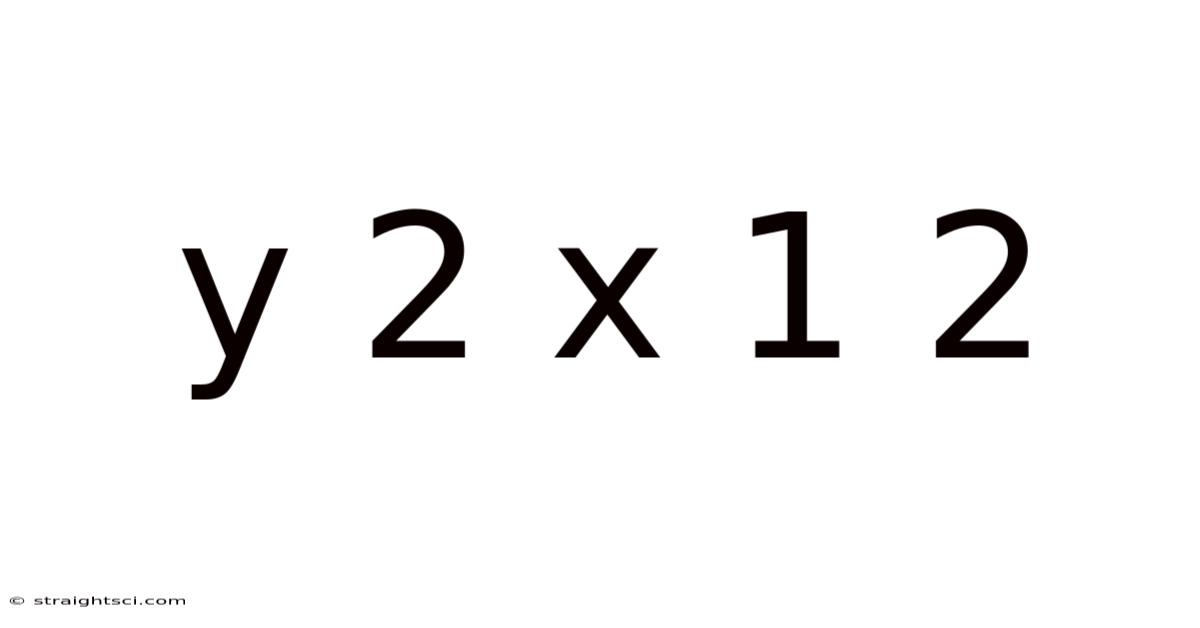
Table of Contents
Decoding the Mystery: A Deep Dive into "Y = 2X + 12"
This article explores the mathematical expression "Y = 2X + 12," demystifying its components, applications, and implications. We'll delve into its graphical representation, its use in various fields, and address frequently asked questions. Understanding this seemingly simple equation opens doors to a broader comprehension of linear algebra and its practical applications in everyday life. This exploration will be suitable for students, educators, and anyone curious about the power of mathematical relationships.
Understanding the Basics: Variables and Constants
At its core, "Y = 2X + 12" is a linear equation. This means it represents a straight line when graphed. Let's break down the components:
-
Y and X: These are variables. They represent unknown quantities that can change. 'Y' is typically considered the dependent variable (its value depends on X), and 'X' is the independent variable (its value is chosen freely).
-
2: This is the coefficient of X. It indicates the rate of change of Y with respect to X. In simpler terms, for every one-unit increase in X, Y increases by two units.
-
12: This is the constant term or y-intercept. It represents the value of Y when X is zero. The line intersects the Y-axis at the point (0, 12).
Graphical Representation: Visualizing the Equation
The beauty of this equation lies in its visual representation. Plotting it on a Cartesian coordinate system reveals a straight line with a specific slope and intercept.
-
Slope: The coefficient of X (2) determines the slope of the line. A positive slope indicates a positive correlation – as X increases, Y increases. The slope of 2 means the line rises 2 units for every 1 unit it moves to the right.
-
Y-intercept: The constant term (12) indicates where the line intersects the Y-axis. This is the point where X = 0.
To graph the equation:
-
Find the y-intercept: When X = 0, Y = 12. Plot the point (0, 12).
-
Find another point: Choose any value for X (e.g., X = 1). Substitute it into the equation: Y = 2(1) + 12 = 14. Plot the point (1, 14).
-
Draw a line: Draw a straight line through the two points you plotted. This line represents the equation Y = 2X + 12.
Real-World Applications: Where Do We See This Equation?
While seemingly abstract, "Y = 2X + 12" finds applications in numerous real-world scenarios:
-
Business and Economics: It can model simple cost functions. Imagine X represents the number of units produced, and Y represents the total cost. The constant term (12) could represent fixed costs (rent, utilities), while the coefficient (2) represents the variable cost per unit.
-
Physics: It can describe uniform motion. If X represents time and Y represents distance, the equation could model an object moving at a constant speed of 2 units of distance per unit of time, starting 12 units away from the origin.
-
Engineering: It can be used in simple linear estimations and predictions in various engineering disciplines. For example, predicting the relationship between input voltage (X) and output current (Y) in a simple circuit (assuming a linear relationship).
-
Data Analysis: In simpler data sets, this equation can be used to perform a linear regression, allowing for basic predictions based on the relationship between two variables.
-
Everyday Life: While less obvious, similar linear relationships exist in many daily situations. For example, the total cost of purchasing apples (Y) where X represents the number of apples, and the price per apple and any initial fee are represented by the coefficient and constant.
Extending the Understanding: Slope-Intercept Form and Other Representations
The equation "Y = 2X + 12" is presented in the slope-intercept form, which is arguably the most intuitive for understanding the slope and y-intercept. However, other forms exist, such as the standard form (Ax + By = C) and point-slope form (y - y1 = m(x - x1)). Understanding these different representations allows for greater flexibility in solving problems and applying the equation in different contexts.
Solving Problems with the Equation: Finding X and Y
We can use the equation to find the value of either variable given the value of the other.
-
Finding Y given X: Simply substitute the known value of X into the equation and solve for Y. For example, if X = 5, then Y = 2(5) + 12 = 22.
-
Finding X given Y: Substitute the known value of Y into the equation and solve for X using algebraic manipulation. For example, if Y = 20, then 20 = 2X + 12. Subtracting 12 from both sides gives 8 = 2X, and dividing by 2 gives X = 4.
Advanced Concepts: Linear Inequalities and Systems of Equations
This equation serves as a foundation for more advanced concepts.
-
Linear Inequalities: Instead of an equals sign, we could have an inequality (>, <, ≥, ≤). This would represent a region on the graph rather than a single line.
-
Systems of Equations: Multiple linear equations can be solved simultaneously to find the intersection point of the lines they represent. This can provide solutions to more complex problems involving multiple variables and relationships.
Frequently Asked Questions (FAQ)
Q: What happens if the coefficient of X is negative?
A: A negative coefficient indicates a negative correlation – as X increases, Y decreases. The line will slope downwards from left to right.
Q: What if the constant term is zero?
A: If the constant term is zero, the line passes through the origin (0, 0). The equation would simplify to Y = 2X.
Q: Can this equation represent a curve?
A: No, this equation specifically represents a straight line. Curved relationships require different types of equations (e.g., quadratic, exponential).
Q: How can I use this equation in a spreadsheet program like Excel or Google Sheets?
A: You can easily create a table with values for X and use the formula (=2*X+12) to calculate the corresponding values for Y. You can then graph this data to visualize the line.
Conclusion: The Power of Simplicity
The seemingly simple equation "Y = 2X + 12" offers a powerful introduction to the world of linear algebra. Understanding its components, graphical representation, and applications broadens our ability to model, analyze, and predict relationships in diverse fields. Its simplicity belies its power, serving as a foundational stepping stone for more complex mathematical concepts and real-world problem-solving. By mastering this equation, we unlock a deeper understanding of the language of mathematics and its ability to illuminate the patterns that shape our world.
Latest Posts
Latest Posts
-
Beans With The Most Iron
Aug 27, 2025
-
4 Km How Many Miles
Aug 27, 2025
-
Pentagons Have How Many Sides
Aug 27, 2025
-
How Much Is 50 Kilos
Aug 27, 2025
-
Whats An Outlier In Math
Aug 27, 2025
Related Post
Thank you for visiting our website which covers about Y 2 X 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.