What Is 20 Of 25
straightsci
Sep 09, 2025 · 5 min read
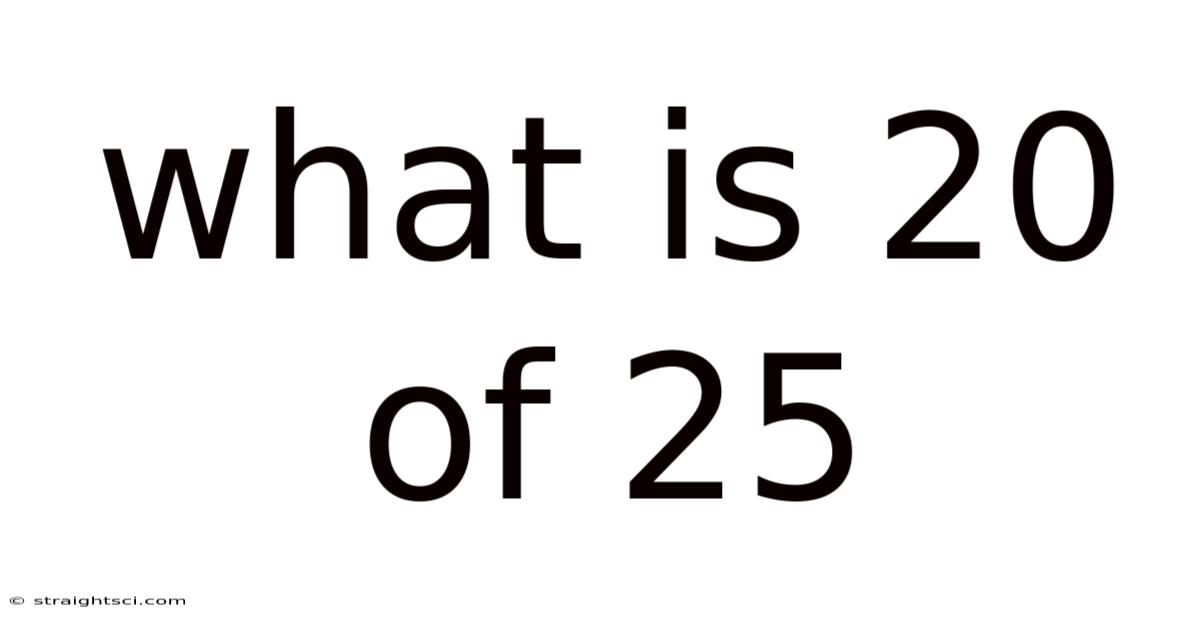
Table of Contents
What is 20 out of 25? Understanding Fractions, Percentages, and Ratios
Finding out "what is 20 out of 25?" might seem like a simple arithmetic problem, but it opens the door to understanding several fundamental mathematical concepts: fractions, percentages, and ratios. This seemingly basic calculation is crucial in many real-world scenarios, from calculating grades to understanding financial data and interpreting statistics. This article will thoroughly explore this question, providing a step-by-step guide, explaining the underlying principles, and offering practical applications.
Understanding the Problem: Fractions, Percentages, and Ratios
The question "what is 20 out of 25?" essentially asks us to express the relationship between 20 and 25 in different mathematical forms. Let's break down each representation:
-
Fraction: A fraction represents a part of a whole. In this case, 20 out of 25 can be written as the fraction 20/25. This means 20 represents the part, and 25 represents the whole.
-
Percentage: A percentage expresses a fraction as a portion of 100. To find the percentage, we need to convert the fraction 20/25 into an equivalent fraction with a denominator of 100, or we can use a simpler method involving decimal conversion.
-
Ratio: A ratio compares two quantities. The ratio of 20 out of 25 is expressed as 20:25. This shows the relationship between the part (20) and the whole (25).
Calculating 20 out of 25 as a Fraction
The simplest way to represent 20 out of 25 is as a fraction: 20/25. However, fractions are often simplified to their lowest terms. To simplify a fraction, we find the greatest common divisor (GCD) of the numerator (20) and the denominator (25). The GCD of 20 and 25 is 5. We divide both the numerator and the denominator by the GCD:
20 ÷ 5 = 4 25 ÷ 5 = 5
Therefore, the simplified fraction is 4/5. This means that 20 out of 25 is equivalent to 4 out of 5.
Converting the Fraction to a Percentage
There are two primary ways to convert the fraction 4/5 (or 20/25) to a percentage:
Method 1: Creating an equivalent fraction with a denominator of 100
To convert a fraction to a percentage, we need to express it as a fraction with a denominator of 100. We can do this by finding an equivalent fraction:
We can multiply both the numerator and the denominator of 4/5 by 20 to get a denominator of 100:
(4 x 20) / (5 x 20) = 80/100
Since 80/100 means 80 out of 100, this is equivalent to 80%.
Method 2: Converting the fraction to a decimal and then to a percentage
First, we convert the fraction 4/5 to a decimal by dividing the numerator by the denominator:
4 ÷ 5 = 0.8
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage sign (%):
0.8 x 100 = 80%
Therefore, 20 out of 25 is 80%.
Expressing 20 out of 25 as a Ratio
A ratio expresses the relationship between two quantities. The ratio of 20 out of 25 is written as 20:25. Like fractions, ratios can be simplified by dividing both parts by their GCD (which is 5):
20 ÷ 5 = 4 25 ÷ 5 = 5
The simplified ratio is 4:5. This indicates that for every 4 parts, there are 5 parts in total.
Real-World Applications of 20 out of 25
Understanding how to calculate and interpret fractions, percentages, and ratios is essential in numerous real-world scenarios:
-
Academic Performance: If a student answers 20 out of 25 questions correctly on a test, their score is 80%. This helps determine their grade and understanding of the subject matter.
-
Financial Calculations: Understanding percentages is crucial for calculating interest rates, discounts, profit margins, and other financial metrics. For example, if you invest $25 and make a profit of $20, your profit margin is 80%.
-
Data Analysis and Statistics: Percentages and ratios are widely used in data analysis to represent proportions and make comparisons. For instance, in a survey of 25 people, if 20 prefer a certain product, the preference rate is 80%.
-
Everyday Calculations: Many everyday situations involve calculating fractions and percentages, such as calculating tips in restaurants, determining sale prices, or dividing food portions.
Further Exploration: Proportions and Problem Solving
The concept of 20 out of 25 extends to broader mathematical concepts like proportions. A proportion is a statement that two ratios are equal. For instance:
20/25 = x/100
To solve for x (the equivalent value out of 100, representing the percentage), we can cross-multiply:
20 * 100 = 25 * x 2000 = 25x x = 2000/25 x = 80
This again confirms that 20 out of 25 is equivalent to 80%. Understanding proportions allows you to solve a wide range of problems involving scaling, ratios, and comparisons.
Frequently Asked Questions (FAQs)
Q: Can I use a calculator to solve this problem?
A: Yes, absolutely! You can use a calculator to divide 20 by 25 to get the decimal 0.8, then multiply by 100 to obtain the percentage 80%. Calculators can also simplify fractions.
Q: What if the numbers were different? How would I approach a similar problem?
A: The same principles apply. For any "X out of Y" problem, you would represent it as a fraction X/Y, simplify it to its lowest terms, and then convert it to a percentage by dividing X by Y and multiplying by 100.
Q: Are there any other ways to represent 20 out of 25?
A: Yes, you could also represent it using a decimal (0.8), a ratio (4:5), or even visually using a pie chart or bar graph.
Conclusion: Mastering the Fundamentals
Determining "what is 20 out of 25?" is more than just a simple calculation; it's a gateway to understanding fundamental mathematical concepts crucial for various applications. By mastering the conversion between fractions, percentages, and ratios, you build a strong foundation for tackling more complex mathematical problems and interpreting data effectively in your daily life, studies, and professional endeavors. The ability to seamlessly transition between these representations allows for a deeper understanding of numerical relationships and enhances problem-solving skills across diverse fields. Remember the core principles outlined here, and you'll find yourself confidently tackling similar calculations and expanding your mathematical proficiency.
Latest Posts
Latest Posts
-
X 4 3x 2 4
Sep 09, 2025
-
How To Find Vertical Asymptote
Sep 09, 2025
-
Edges In A Rectangular Prism
Sep 09, 2025
-
How Many Edges For Cylinder
Sep 09, 2025
-
X Linked Dominant Pedigree Chart
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.