X 4 3x 2 4
straightsci
Sep 09, 2025 · 5 min read
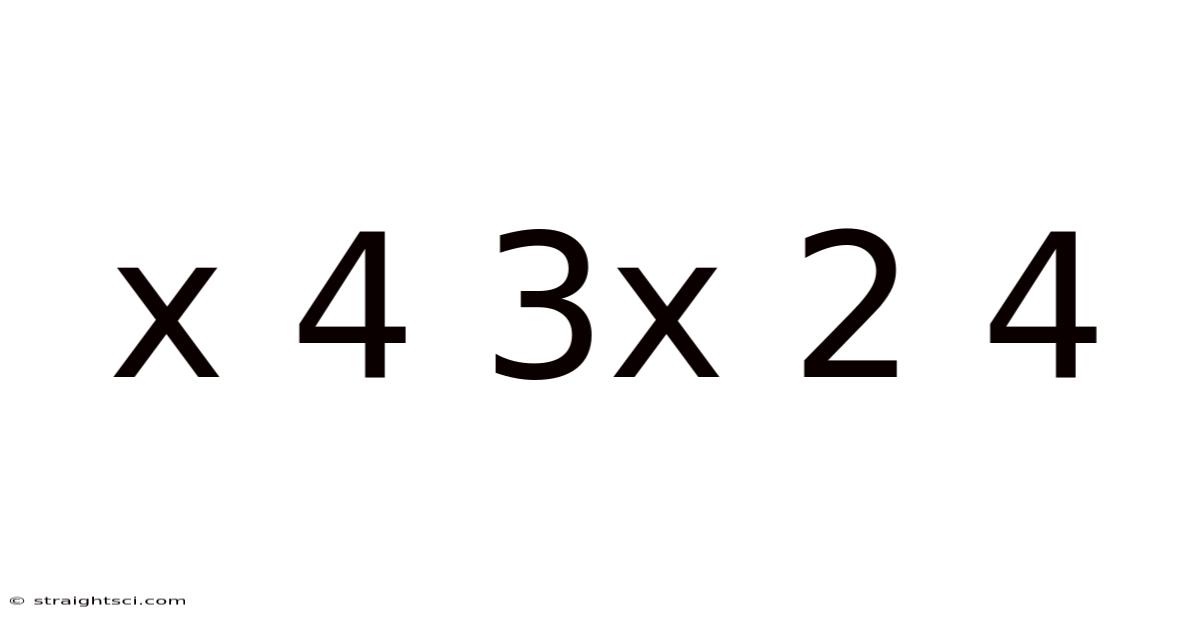
Table of Contents
Decoding the Mathematical Enigma: x⁴ + 3x² + 4
This article delves into the fascinating world of polynomial equations, specifically focusing on the seemingly simple yet surprisingly complex expression: x⁴ + 3x² + 4. We'll explore its properties, potential solutions, and the mathematical techniques needed to understand it fully. Understanding this seemingly simple equation provides a strong foundation for tackling more advanced algebraic concepts. This exploration will cover various approaches, suitable for students from intermediate algebra to those pursuing higher-level mathematics.
Introduction: Understanding the Polynomial
The expression x⁴ + 3x² + 4 is a quartic polynomial, meaning it's a polynomial of degree four. The highest power of the variable x is 4. Notice that it's missing the x³ and x terms, simplifying its appearance but not necessarily its complexity. Our goal is to understand how to solve this equation, which means finding the values of x that make the equation equal to zero: x⁴ + 3x² + 4 = 0. This seemingly straightforward equation holds some interesting mathematical nuances.
Method 1: Substitution and the Quadratic Formula
One approach to solving this quartic equation is through a clever substitution. Let's substitute u = x². This transforms our quartic equation into a quadratic equation:
u² + 3u + 4 = 0
This is a much more manageable equation! We can now use the well-known quadratic formula to solve for u:
u = [-b ± √(b² - 4ac)] / 2a
Where a = 1, b = 3, and c = 4. Plugging in these values, we get:
u = [-3 ± √(3² - 4 * 1 * 4)] / 2 * 1
u = [-3 ± √(-7)] / 2
Notice that we have a negative number under the square root. This indicates that the solutions for u are complex numbers. Specifically:
u₁ = (-3 + i√7) / 2 u₂ = (-3 - i√7) / 2
where i represents the imaginary unit (√-1).
Method 2: Finding the Roots (Solutions)
Now that we have the values of u, we can substitute back to find the values of x:
Remember that u = x². Therefore:
x² = (-3 + i√7) / 2 and x² = (-3 - i√7) / 2
To solve for x, we need to take the square root of each of these complex numbers. This will result in four distinct solutions (roots) for x, because each complex number has two square roots. The solutions will also be complex numbers. Calculating these square roots requires a bit more advanced complex number arithmetic, often involving polar form or De Moivre's theorem.
The Nature of Complex Roots
The fact that we obtain complex roots is not unusual for polynomial equations of degree higher than two. Complex numbers are an extension of the real number system, necessary to represent solutions to equations that don't have real-number solutions. These complex roots always come in conjugate pairs. This means if a + bi is a root, then a - bi is also a root (where a and b are real numbers, and i is the imaginary unit).
Method 3: Factorization (A Challenging Approach)
While substitution is the most efficient method in this case, it's worth noting that factorization can be used to solve polynomial equations. However, factoring this particular quartic polynomial is not straightforward and would likely involve advanced techniques. It's unlikely to be easily factored using elementary methods.
A Deeper Dive into Complex Numbers
The solutions we obtained are complex numbers. Let's review their structure: a complex number is typically represented as a + bi, where a is the real part and b is the imaginary part. The imaginary unit, i, is defined as the square root of -1.
Complex numbers are essential in many areas of mathematics, physics, and engineering. Their importance lies in their ability to represent solutions to equations that lack real-number solutions, expanding the realm of mathematical problem-solving.
Graphical Representation
While visually representing a quartic equation with complex roots on a standard Cartesian coordinate system is impossible, we can visualize aspects of it. Consider plotting the real part of the polynomial against the real values of x. You won't see the complex roots, but the behavior of the graph will still reveal important characteristics, such as its overall shape and any real turning points. However, to fully represent the roots, we would need to use a four-dimensional space.
The Significance of the Equation
This seemingly simple equation, x⁴ + 3x² + 4 = 0, illustrates several key mathematical concepts:
- Polynomial equations: It demonstrates the characteristics and solution methods for higher-order polynomial equations.
- Complex numbers: The equation highlights the importance and necessity of complex numbers in extending solutions beyond the real number system.
- Substitution techniques: It shows how a clever substitution can simplify a complex problem into a more manageable one.
- The quadratic formula: This equation reinforces the importance and widespread applicability of the quadratic formula.
Frequently Asked Questions (FAQs)
Q: Can this equation be solved without using complex numbers?
A: No. The discriminant of the quadratic equation derived through substitution is negative, leading inevitably to complex solutions for x. There are no real-number solutions to this quartic equation.
Q: What are some real-world applications of solving quartic equations?
A: Quartic equations appear in various fields, including physics (modeling oscillations and vibrations), engineering (designing structures and circuits), and computer graphics (creating curves and surfaces).
Q: Are there other methods to solve quartic equations besides substitution?
A: Yes, more advanced methods exist, such as using the Ferrari method or resolvents. These methods are generally more complex and are usually introduced in advanced algebra courses.
Q: What if the constant term (4) was different? Would that change the nature of the solutions?
A: Yes, changing the constant term would alter the values of the roots, potentially influencing whether the solutions are real or complex. A different constant could lead to real roots, complex roots, or a mix of both.
Conclusion: A Stepping Stone to Advanced Mathematics
This exploration of the equation x⁴ + 3x² + 4 = 0 provided a detailed look into solving quartic equations and the significance of complex numbers. This seemingly simple equation serves as a powerful example of how even seemingly basic mathematical expressions can lead to profound insights into advanced mathematical concepts. Mastering the techniques used here forms a strong foundation for tackling even more challenging problems in algebra and beyond. The ability to handle complex numbers and understand the implications of their presence in solutions is crucial for progress in higher mathematics and its applications. The journey of solving this equation serves as a valuable stepping stone to mastering the intricacies of advanced mathematical concepts.
Latest Posts
Latest Posts
-
How To Compute Marginal Revenue
Sep 09, 2025
-
Feels Heavy On My Chest
Sep 09, 2025
-
Number Of Protons In Titanium
Sep 09, 2025
-
What Is A Chemical Bond
Sep 09, 2025
-
Chain Rule In Leibniz Notation
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about X 4 3x 2 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.