Is 1/4 Greater Than 3/8
straightsci
Sep 07, 2025 · 5 min read
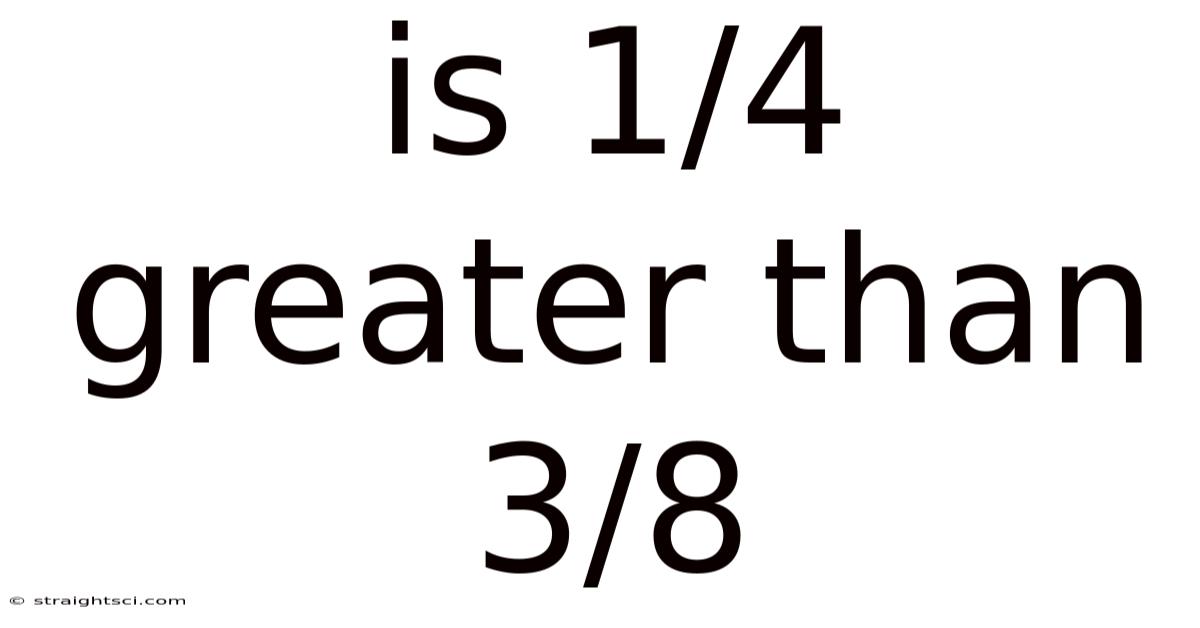
Table of Contents
Is 1/4 Greater Than 3/8? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for everyday life and further academic pursuits. This article will thoroughly explore the question, "Is 1/4 greater than 3/8?", not just providing a simple answer, but delving into the methods for comparing fractions, the underlying mathematical principles, and practical applications. We'll cover various techniques to ensure you confidently tackle similar comparisons in the future.
Introduction: Understanding Fractions
Before directly comparing 1/4 and 3/8, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 1/4, the whole is divided into four equal parts, and we're considering one of those parts.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. This means expressing both fractions with the same denominator. The easiest common denominator to find is usually the least common multiple (LCM) of the two denominators.
Let's compare 1/4 and 3/8:
- The denominators are 4 and 8.
- The multiples of 4 are: 4, 8, 12, 16...
- The multiples of 8 are: 8, 16, 24...
- The least common multiple of 4 and 8 is 8.
Now we need to rewrite both fractions with a denominator of 8:
- 1/4 can be rewritten as 2/8 (multiply both numerator and denominator by 2).
- 3/8 remains as 3/8.
Now the comparison is straightforward: 2/8 versus 3/8. Since 2 is less than 3, we conclude that 2/8 (or 1/4) is less than 3/8.
Method 2: Converting to Decimals
Another way to compare fractions is to convert them into decimals. This involves dividing the numerator by the denominator.
- 1/4 = 1 ÷ 4 = 0.25
- 3/8 = 3 ÷ 8 = 0.375
Comparing the decimal values, 0.25 and 0.375, it's clear that 0.25 (or 1/4) is less than 0.375 (or 3/8).
Method 3: Visual Representation
Visual aids can be incredibly helpful, especially for beginners. Imagine two identical pizzas.
- Cut the first pizza into four equal slices. One slice represents 1/4.
- Cut the second pizza into eight equal slices. Three slices represent 3/8.
By visually comparing the slices, you can see that three slices from the second pizza (3/8) are larger than one slice from the first pizza (1/4). This confirms that 1/4 is less than 3/8.
Explanation using the Number Line
Placing fractions on a number line provides a clear visual representation of their relative sizes. A number line ranging from 0 to 1, divided into increments of 1/8, would show that 1/4 (equivalent to 2/8) lies to the left of 3/8, further illustrating that 1/4 is smaller.
The Importance of Equivalent Fractions
The concept of equivalent fractions is fundamental to comparing fractions. Equivalent fractions represent the same value but have different numerators and denominators. For instance, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions. Understanding equivalence allows you to manipulate fractions to find a common denominator or simplify them to their simplest form.
Simplifying Fractions
Simplifying a fraction means reducing it to its lowest terms. This is done by dividing both the numerator and denominator by their greatest common divisor (GCD). For example, 4/8 can be simplified to 1/2 by dividing both 4 and 8 by their GCD, which is 4. While not directly relevant to this specific comparison, simplifying fractions is a vital skill for working with fractions efficiently.
Practical Applications: Real-World Examples
Understanding fraction comparison is not just an academic exercise; it has numerous real-world applications. Consider these examples:
- Baking: A recipe might call for 1/4 cup of sugar and 3/8 cup of flour. You need to know which quantity is greater to understand the proportions correctly.
- Measurement: If you're measuring lengths using fractions of inches or centimeters, accurate comparison is crucial for precision.
- Sharing: Dividing a pizza or cake fairly amongst friends requires understanding fractions and their relative values.
- Finance: Understanding fractions is essential when dealing with percentages, interest rates, and parts of a whole in financial calculations.
Frequently Asked Questions (FAQs)
Q1: What if the denominators have no common factors other than 1?
If the denominators are relatively prime (meaning their greatest common divisor is 1), you can simply multiply the numerator and denominator of each fraction by the other fraction's denominator to find a common denominator.
Q2: Are there other methods for comparing fractions?
While the methods discussed above are the most common and straightforward, more advanced techniques, such as cross-multiplication, can also be used for comparison.
Q3: How can I improve my fraction skills?
Practice is key! Work through various exercises, solve problems involving fractions, and use visual aids to reinforce your understanding.
Q4: What resources are available to learn more about fractions?
Numerous online resources, textbooks, and educational videos are available to help you deepen your understanding of fractions and related concepts.
Conclusion: Mastering Fraction Comparison
This comprehensive exploration of the question, "Is 1/4 greater than 3/8?", has demonstrated that 1/4 is not greater than 3/8; it is actually less than 3/8. We have covered multiple methods for comparing fractions, emphasizing the importance of finding a common denominator and converting to decimals. Beyond the simple answer, we have delved into the underlying mathematical principles, showcased real-world applications, and addressed frequently asked questions. By understanding these concepts and practicing regularly, you'll develop a solid foundation in fractions and confidently tackle any fraction comparison problem you encounter. Remember, mastering fractions is a building block for success in higher-level mathematics and various practical applications throughout your life.
Latest Posts
Latest Posts
-
X 2 Times X 2
Sep 08, 2025
-
Subtract Whole Numbers From Fractions
Sep 08, 2025
-
What Is A Passive Immunity
Sep 08, 2025
-
400 F Is What C
Sep 08, 2025
-
Functions Of Peripheral Membrane Proteins
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about Is 1/4 Greater Than 3/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.