X 2 Times X 2
straightsci
Sep 08, 2025 · 6 min read
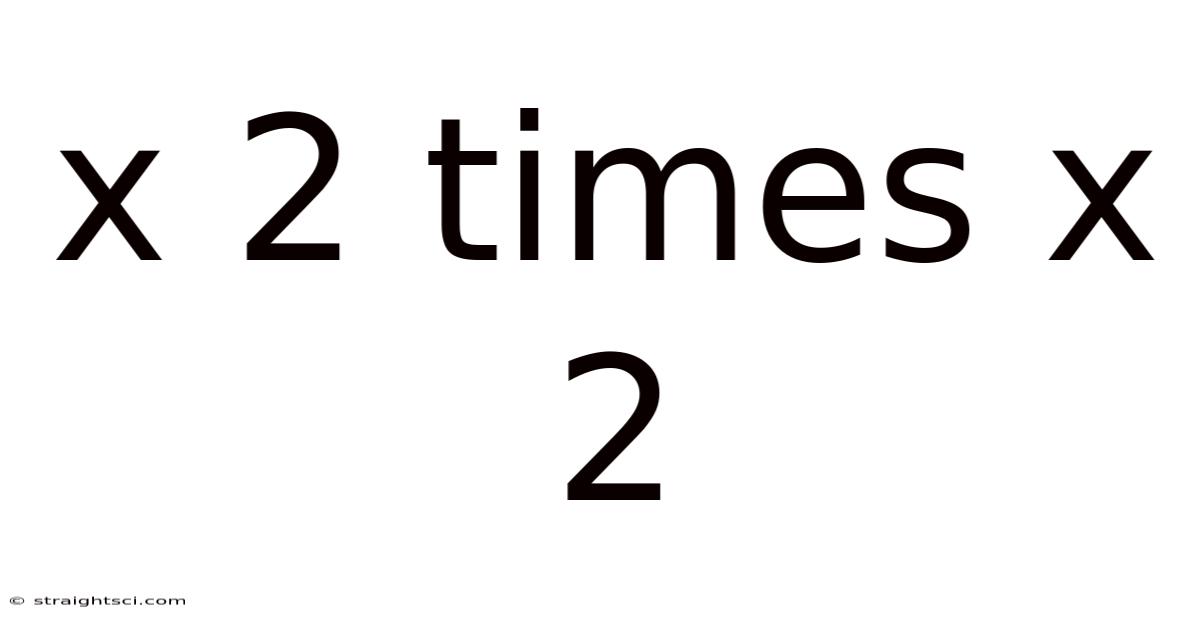
Table of Contents
Decoding "x 2 Times x 2": Exploring Repeated Multiplication and its Applications
Understanding the concept of "x 2 times x 2" goes beyond simple multiplication; it delves into the fundamentals of repeated operations, exponential growth, and its widespread applications in various fields. This seemingly straightforward phrase unlocks a deeper understanding of mathematical principles that underpin many aspects of our world, from calculating compound interest to understanding population growth. This article will explore this concept comprehensively, breaking down the mechanics, illustrating its applications, and answering frequently asked questions.
Introduction: Beyond Basic Multiplication
At its core, "x 2 times x 2" signifies repeated multiplication. It's not simply multiplying a number by 2 twice; it's about understanding the underlying structure of exponential growth and how it manifests in various contexts. This concept is crucial in mathematics, science, finance, and even everyday life. Whether you're calculating the area of a square, predicting population growth, or understanding compound interest, grasping the principles behind repeated multiplication is key. We'll explore these applications in detail throughout this article.
Understanding the Mechanics: Step-by-Step Explanation
Let's break down the phrase "x 2 times x 2" step-by-step, using a variable 'x' to represent any number:
-
x 2: This is a simple multiplication. You take the value of 'x' and multiply it by 2. For example, if x = 5, then x 2 = 10.
-
(x 2) times 2: This is where the repeated multiplication comes in. We take the result of the first step (x 2) and multiply it again by 2. Using the previous example (x=5), this becomes (10) times 2 = 20.
-
Alternative Representation: The phrase "x 2 times x 2" can also be written as 2 * (2 * x) or 2*(2x) or even 4x. This highlights the underlying principle of repeated multiplication leading to a simplified expression. The final answer is always four times the original value of x.
Example 1:
Let's say x = 3.
- x 2 = 3 * 2 = 6
- (x 2) times 2 = 6 * 2 = 12
Example 2:
Let's say x = 10.
- x 2 = 10 * 2 = 20
- (x 2) times 2 = 20 * 2 = 40
The Power of Exponents: A Deeper Dive
The expression "x 2 times x 2" can be elegantly represented using exponents. We can rewrite it as 2²(x) or 4x. This highlights the power of exponential notation in simplifying and generalizing repeated multiplication. In this case, we're essentially raising 2 to the power of 2 (2²) and then multiplying the result by x.
This understanding of exponents is crucial for extending this concept to more complex scenarios. For instance, imagine the phrase: "x 3 times x 3". This translates to 3*(3*x) or 9x which is equivalent to 3²x. Understanding exponents provides a concise and powerful way to represent repeated multiplication, regardless of the number of repetitions or the base number.
Real-World Applications: Where This Concept Matters
The principle of "x 2 times x 2"—and its broader application of repeated multiplication—appears in numerous real-world scenarios:
-
Compound Interest: Compound interest is the interest earned on both the principal amount and the accumulated interest from previous periods. The formula for compound interest involves repeated multiplication, similar to the concept we've explored. Each period, the interest is added to the principal, and the next period's interest is calculated on this larger amount, leading to exponential growth.
-
Population Growth: Population growth, especially in scenarios with high birth rates, can be modeled using exponential functions. If a population doubles every generation (a simplified model), the growth mirrors the "x 2 times x 2" principle. Repeated doubling leads to a rapid increase in population size.
-
Geometric Sequences: In mathematics, a geometric sequence is a sequence where each term is found by multiplying the previous term by a constant value. The "x 2 times x 2" concept perfectly fits into this framework, representing a simple geometric sequence with a common ratio of 2.
-
Area Calculations: Consider calculating the area of a square. If you double the side length of a square (x), and then double it again, you’ll find the area grows according to this principle. The initial area is x², doubling the side length once gives (2x)², and doubling it again gives (4x)², demonstrating the effect of repeated multiplication on area.
-
Scientific Modeling: Many scientific models, such as those describing radioactive decay or the spread of infectious diseases, utilize exponential functions based on repeated multiplication. These models rely heavily on the principles we've discussed.
Beyond "x 2 Times x 2": Generalizing the Concept
The concept of "x 2 times x 2" is easily generalized to other repeated multiplication scenarios. Instead of multiplying by 2 twice, we could multiply by any number (let's say 'n') any number of times (let's say 'm'). This can be expressed as n<sup>m</sup>x. This illustrates the broader applicability of exponential functions and repeated multiplication in various mathematical and scientific contexts.
Frequently Asked Questions (FAQ)
Q1: What if I multiply x by 2 three times?
A1: Multiplying x by 2 three times would be represented as x * 2 * 2 * 2, which is equivalent to 8x or 2³x. This demonstrates the exponential growth as the number of repetitions increases.
Q2: How is this different from simply multiplying x by 4?
A2: While both "x 2 times x 2" and "x * 4" result in the same numerical answer (4x), the underlying conceptual difference is significant. "x 2 times x 2" emphasizes the process of repeated multiplication, highlighting the exponential nature of the operation and its relevance in models like compound interest or population growth. "x * 4" is a simpler, single-step multiplication, devoid of the repeated operation aspect.
Q3: Can this be applied to numbers other than 2?
A3: Absolutely! The principle of repeated multiplication applies to any number. For instance, "x 3 times x 3" would be x * 3 * 3 = 9x or 3²x, and so on. The underlying concept of repeated multiplication and its exponential nature remains consistent.
Q4: Are there any limitations to this concept?
A4: While the concept is broadly applicable, its direct application might be limited in situations with non-constant growth rates or factors that introduce variability into the process. More complex mathematical models are required in such cases.
Conclusion: The Significance of Repeated Multiplication
Understanding the concept of "x 2 times x 2" provides a fundamental grasp of repeated multiplication, exponential growth, and its widespread implications in various disciplines. From calculating compound interest to modeling population dynamics, the principles discussed here are essential for comprehending and analyzing various real-world phenomena. The ability to recognize and apply this concept enables a deeper understanding of the mathematical structures that govern much of our world. By mastering this fundamental concept, you build a solid foundation for tackling more complex mathematical and scientific challenges. The seemingly simple phrase "x 2 times x 2" opens a door to a wide array of mathematical and scientific applications, enhancing your problem-solving skills and understanding of the world around you.
Latest Posts
Latest Posts
-
How Many Teaspoons Is 3ml
Sep 08, 2025
-
Horizontal Asymptote Of Rational Function
Sep 08, 2025
-
Difference Soluble And Insoluble Fibre
Sep 08, 2025
-
9 16th On A Tape Measure
Sep 08, 2025
-
Muscularis Layer Of The Stomach
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about X 2 Times X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.