Is 1/4 Bigger Than 3/4
straightsci
Sep 12, 2025 · 5 min read
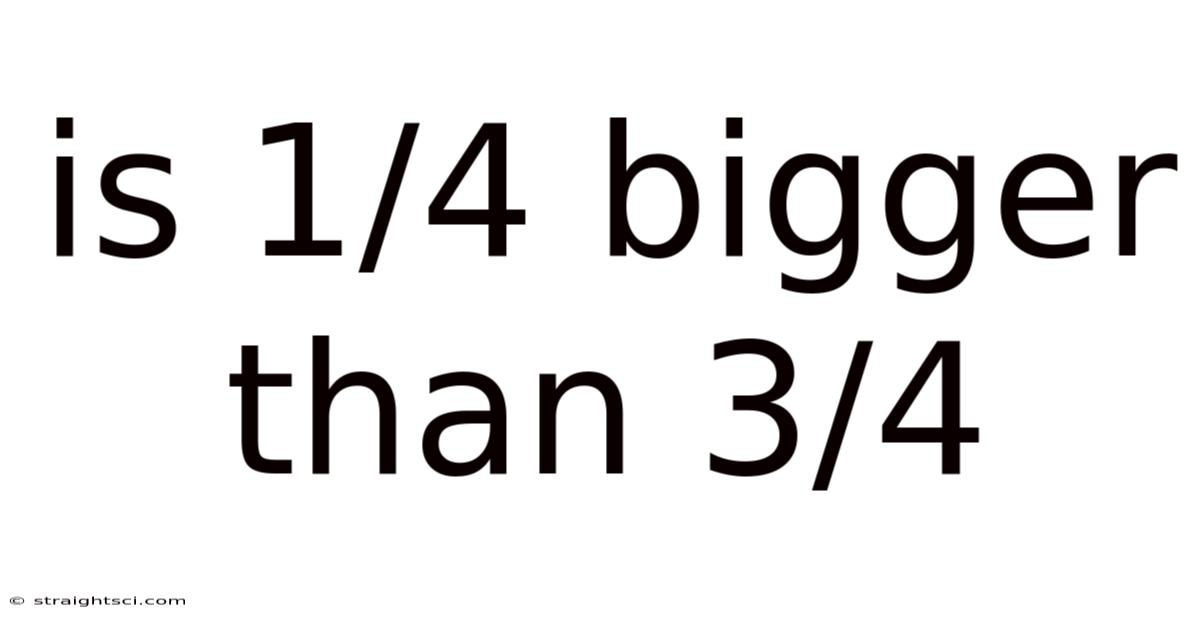
Table of Contents
Is 1/4 Bigger Than 3/4? Understanding Fractions and Comparisons
Is 1/4 bigger than 3/4? The answer might seem obvious to some, but understanding why one fraction is larger than another is crucial for mastering fundamental math concepts. This article will delve into the world of fractions, explaining how to compare them, and debunking the misconception that 1/4 could ever be bigger than 3/4. We'll explore different methods for comparing fractions, including visual representations and numerical comparisons, ensuring a comprehensive understanding suitable for learners of all levels.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's revisit the basics of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), like this: a/b. The numerator (a) indicates how many parts you have, while the denominator (b) indicates how many equal parts the whole is divided into.
For example, in the fraction 1/4, the numerator (1) tells us we have one part, and the denominator (4) tells us the whole is divided into four equal parts. Similarly, in 3/4, we have three parts out of a whole divided into four equal parts.
Visualizing Fractions: The Pizza Analogy
One of the best ways to understand fractions is through visual aids. Imagine a pizza cut into four equal slices.
- 1/4: This represents one slice of the pizza out of the four total slices.
- 3/4: This represents three slices of the pizza out of the four total slices.
Looking at this visual representation, it's instantly clear that 3/4 (three slices) is significantly larger than 1/4 (one slice). This simple visual analogy makes the comparison intuitive and easy to grasp.
Comparing Fractions: Different Methods
While visual aids are helpful, we need a more robust method for comparing fractions, especially when dealing with more complex numbers. Here are a few approaches:
1. Same Denominator:
The easiest way to compare fractions is when they share the same denominator. If the denominators are identical, the fraction with the larger numerator is the larger fraction. In our example, both 1/4 and 3/4 have the same denominator (4). Since 3 > 1, 3/4 is larger than 1/4.
2. Same Numerator (Less Common but Applicable):
If the numerators are the same, the fraction with the smaller denominator is the larger fraction. For instance, 3/4 is larger than 3/8 because the whole is divided into fewer parts in 3/4, meaning each part is larger.
3. Finding a Common Denominator:
This is the most general method for comparing fractions with different denominators. To compare fractions like 2/3 and 3/5, we find the least common multiple (LCM) of the denominators (3 and 5). The LCM of 3 and 5 is 15. We then convert both fractions to have a denominator of 15:
- 2/3 = (2 x 5) / (3 x 5) = 10/15
- 3/5 = (3 x 3) / (5 x 3) = 9/15
Now, we can easily compare: 10/15 > 9/15, therefore 2/3 > 3/5.
4. Converting to Decimals:
Another method is to convert the fractions into decimals. This can be done by dividing the numerator by the denominator:
- 1/4 = 0.25
- 3/4 = 0.75
Clearly, 0.75 > 0.25, confirming that 3/4 is larger than 1/4.
The Number Line: A Visual Representation of Comparison
A number line can also be a valuable tool for visualizing and comparing fractions. Place 0 and 1 on the number line. Then, divide the space between 0 and 1 into equal parts based on the denominators of the fractions. You can then easily locate the fractions on the line and compare their positions. For 1/4 and 3/4, you would divide the space between 0 and 1 into four equal parts. 1/4 will be located at the first mark, and 3/4 at the third mark, clearly showing that 3/4 is further along the line, indicating a greater value.
Addressing the Misconception: Why 1/4 is NOT Bigger Than 3/4
The misconception that 1/4 might be bigger than 3/4 likely stems from a misunderstanding of the fundamental principles of fractions. It's crucial to remember that the denominator represents the total number of equal parts, and the numerator represents the number of parts considered. In the context of 1/4 and 3/4, both fractions refer to the same whole, divided into four equal parts. Therefore, having three parts (3/4) is always larger than having only one part (1/4).
Common Mistakes in Fraction Comparison
Many errors in comparing fractions arise from neglecting fundamental concepts. Here are some common pitfalls:
- Ignoring the denominator: Students may focus solely on the numerators and incorrectly assume that a larger numerator always means a larger fraction.
- Incorrectly finding common denominators: Errors in calculation when finding the least common multiple can lead to incorrect comparisons.
- Misunderstanding the concept of the whole: Failing to appreciate that the fractions represent parts of the same whole leads to flawed comparisons.
Frequently Asked Questions (FAQ)
Q1: Can fractions be compared if they have different denominators and numerators?
A1: Yes, absolutely! The methods outlined above, such as finding a common denominator or converting to decimals, work effectively for comparing fractions with different denominators and numerators.
Q2: Is there a shortcut for comparing fractions with large numbers?
A2: While there isn't a single universally quick shortcut, converting fractions to decimals can often be faster for large numbers, especially if you have a calculator. However, understanding the core concepts of finding a common denominator remains a valuable skill.
Q3: How can I help my child understand fraction comparison?
A3: Use visual aids like pizza slices or blocks to represent fractions. Start with simple examples and gradually increase complexity. Make the learning process interactive and engaging. Use number lines and practice problems to reinforce understanding.
Conclusion: Mastering Fraction Comparison
Understanding fraction comparison is a cornerstone of mathematical proficiency. By mastering the techniques discussed in this article – using visual aids, finding common denominators, converting to decimals, and utilizing the number line – you'll develop a solid foundation for more advanced mathematical concepts. Remember, 1/4 is definitively smaller than 3/4. The key is to grasp the relationship between the numerator and the denominator and to employ consistent methods for accurate comparison. With practice and a clear understanding of the principles, comparing fractions will become second nature.
Latest Posts
Latest Posts
-
What Does Ram Stand For
Sep 12, 2025
-
How To Find Mean Deviation
Sep 12, 2025
-
Can You Flush A Condom
Sep 12, 2025
-
1 4 On Tape Measure
Sep 12, 2025
-
How Do I Measure Angles
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Is 1/4 Bigger Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.