Is 1/3 Bigger Than 1/2
straightsci
Sep 17, 2025 · 6 min read
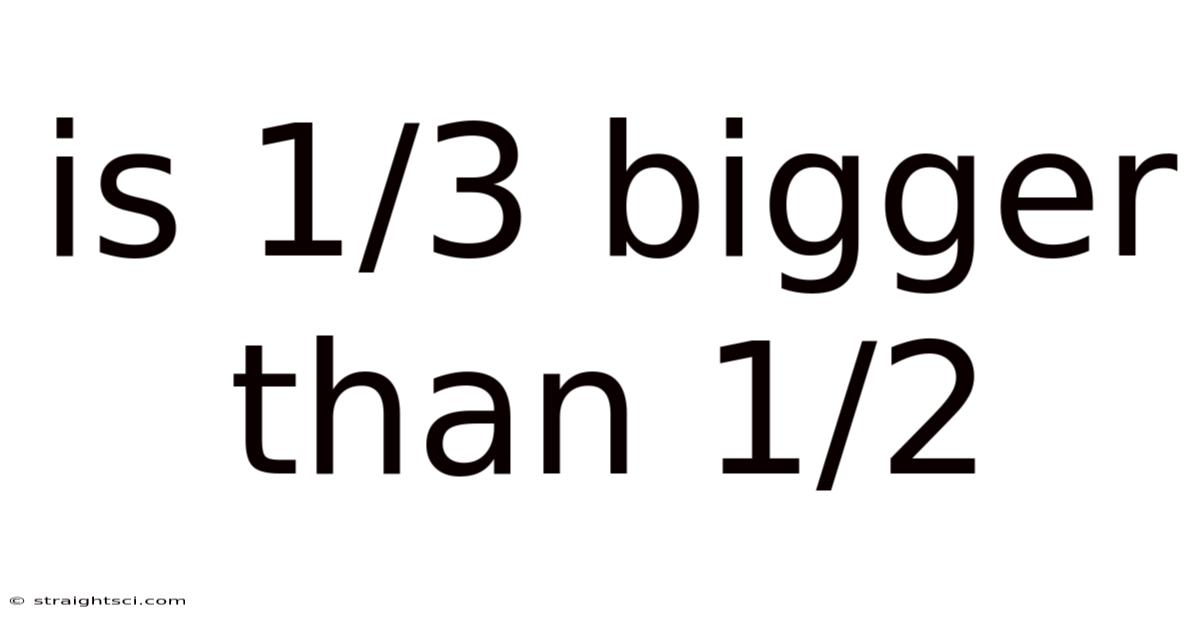
Table of Contents
Is 1/3 Bigger Than 1/2? Understanding Fractions and Comparisons
Is 1/3 bigger than 1/2? The answer might seem obvious to some, but understanding why one fraction is larger than another is crucial for developing a strong foundation in mathematics. This article delves deep into the concept of comparing fractions, providing explanations suitable for learners of all levels, from elementary school students to those brushing up on their fundamental math skills. We'll explore various methods for comparing fractions, discuss the underlying principles, and address common misconceptions.
Understanding Fractions: A Quick Refresher
Before we tackle the core question, let's review the basics of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator tells us how many equal parts the whole is divided into, while the numerator tells us how many of those parts we're considering.
For example, in the fraction 1/2, the denominator (2) indicates that the whole is divided into two equal parts, and the numerator (1) indicates that we are considering one of those parts. Similarly, 1/3 represents one part of a whole divided into three equal parts.
Comparing Fractions: Visual Representation
One of the easiest ways to compare fractions like 1/3 and 1/2 is through visual representation. Imagine two identical circles.
- Circle 1: Divide this circle into two equal halves. Shade one half. This visually represents 1/2.
- Circle 2: Divide this circle into three equal thirds. Shade one third. This visually represents 1/3.
By comparing the shaded areas of both circles, it's immediately clear that the shaded area representing 1/2 is significantly larger than the shaded area representing 1/3. This visual comparison provides a concrete understanding of why 1/2 is greater than 1/3.
Comparing Fractions: Numerical Methods
While visual representations are helpful, especially for beginners, we also need numerical methods for comparing fractions, especially when dealing with more complex fractions. Here are a few approaches:
-
Finding a Common Denominator: This is perhaps the most common and reliable method. To compare 1/3 and 1/2, we need to find a common denominator – a number that is a multiple of both 3 and 2. The least common multiple (LCM) of 3 and 2 is 6.
- We convert 1/2 to an equivalent fraction with a denominator of 6: (1/2) * (3/3) = 3/6
- We convert 1/3 to an equivalent fraction with a denominator of 6: (1/3) * (2/2) = 2/6
Now, comparing 3/6 and 2/6, it's evident that 3/6 > 2/6, meaning 1/2 > 1/3.
-
Comparing Numerators with the Same Denominator: If two fractions have the same denominator, the fraction with the larger numerator is the larger fraction. This method is straightforward and intuitive.
-
Comparing Denominators with the Same Numerator: If two fractions have the same numerator, the fraction with the smaller denominator is the larger fraction. This is because a smaller denominator implies larger individual parts. For example, 1/2 is larger than 1/3 because each half is larger than each third.
The Importance of Equivalent Fractions
The concept of equivalent fractions is crucial for comparing fractions. Equivalent fractions represent the same value but have different numerators and denominators. For instance, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions. Understanding equivalent fractions allows us to rewrite fractions in a form that makes comparison easier.
Addressing Common Misconceptions
Several misconceptions frequently arise when comparing fractions:
-
Focusing solely on the Numerator: Some students mistakenly believe that because the numerator in 1/3 is smaller than the numerator in 1/2, 1/3 is automatically smaller. This is incorrect; the denominator plays an equally crucial role.
-
Ignoring the Denominator: Similarly, some might overlook the denominator altogether, leading to inaccurate comparisons.
-
Difficulty with Common Denominators: Finding a common denominator can be challenging for some students, particularly when dealing with larger numbers. Practice and understanding the concept of LCM are essential to overcome this obstacle.
Extending the Concept: Comparing More Complex Fractions
The methods discussed above can be extended to compare more complex fractions. For instance, to compare 5/8 and 3/4, we follow these steps:
- Find a common denominator: The LCM of 8 and 4 is 8.
- Convert fractions to equivalent fractions: 3/4 = (3/4) * (2/2) = 6/8
- Compare: 5/8 < 6/8, therefore 5/8 < 3/4.
Decimal Representation and Fraction Comparison
Fractions can also be converted to decimals to facilitate comparison. 1/2 = 0.5 and 1/3 = 0.333... (a repeating decimal). It's clear that 0.5 > 0.333..., confirming that 1/2 > 1/3. This method is particularly useful when dealing with fractions that are difficult to compare using common denominators.
Practical Applications of Fraction Comparison
Understanding fraction comparison is crucial in various real-life situations:
-
Cooking and Baking: Recipes often require precise measurements, often expressed as fractions. Knowing which fraction is larger ensures accurate ingredient proportions.
-
Measurement and Construction: In carpentry, engineering, and other construction fields, precise measurements are paramount. Comparing fractions is essential for accuracy and efficiency.
-
Data Analysis: Fractions are frequently used to represent proportions and percentages in data analysis. Comparing fractions allows for meaningful interpretations and comparisons of different datasets.
-
Financial Literacy: Understanding fractions is vital for managing personal finances. Comparing fractions helps in understanding loan interest rates, discounts, and investment returns.
Frequently Asked Questions (FAQ)
-
Q: Is there a quick way to compare fractions without finding a common denominator?
- A: While finding a common denominator is the most reliable method, if both fractions have the same numerator or denominator, you can compare them directly, as explained above. Estimating the value of each fraction can sometimes provide a quick, albeit less precise, comparison.
-
Q: How do I compare fractions with different numerators and denominators?
- A: The most reliable method is to find a common denominator and convert the fractions to equivalent fractions with that common denominator. Then compare the numerators.
-
Q: What if I have a mixed number and a fraction to compare?
- A: Convert the mixed number into an improper fraction (where the numerator is larger than the denominator). Then, use the common denominator method to compare them.
-
Q: Are there any online tools that can help me compare fractions?
- A: While this article avoids external links, many educational websites offer online fraction calculators and comparison tools. These tools can be beneficial for practicing and checking your work.
Conclusion: Mastering Fraction Comparison
The question "Is 1/3 bigger than 1/2?" serves as a gateway to understanding a fundamental concept in mathematics: comparing fractions. By mastering the techniques of finding a common denominator, understanding equivalent fractions, and visualizing fractional representations, you gain a powerful tool for solving various mathematical problems and tackling real-world scenarios that require a firm grasp of fractions. Remember, practice is key to building confidence and proficiency in comparing fractions. Consistent effort will lead to a deeper understanding and greater mathematical fluency. Don't hesitate to revisit these concepts and practice regularly to solidify your understanding.
Latest Posts
Latest Posts
-
Where To Stick Thermometer Turkey
Sep 17, 2025
-
15 000 Steps In Calories
Sep 17, 2025
-
What Number Month Is August
Sep 17, 2025
-
3 4 Cup Divided In Half
Sep 17, 2025
-
4 Main Islands Of Japan
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Is 1/3 Bigger Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.