3/4 Cup Divided In Half
straightsci
Sep 17, 2025 · 5 min read
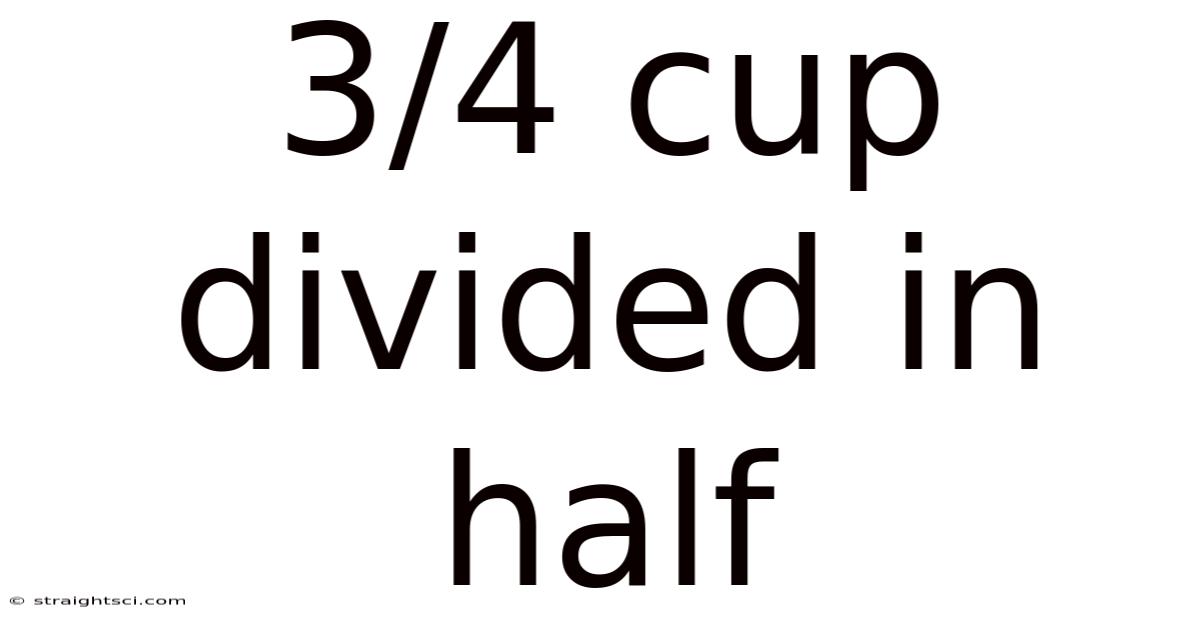
Table of Contents
Dividing 3/4 Cup: A Comprehensive Guide to Fraction Division in Cooking and Beyond
Dividing 3/4 of a cup in half might seem like a simple task, a piece of cake even. But understanding the underlying principles of fraction division is crucial not only in cooking and baking, where precise measurements are key, but also in various aspects of mathematics and everyday life. This comprehensive guide will break down exactly how to divide 3/4 cup in half, explore the mathematical concepts involved, and extend the understanding to more complex fraction divisions.
Introduction: Understanding Fractions and Division
Before we tackle the specific problem of dividing 3/4 cup in half, let's refresh our understanding of fractions and division. A fraction represents a part of a whole. In the case of 3/4 cup, the "4" represents the total number of equal parts the whole cup is divided into, and the "3" represents the number of parts we're considering. Division, on the other hand, is the process of splitting a quantity into equal parts. When we divide 3/4 cup in half, we're essentially finding what one-half of 3/4 is.
Method 1: The Visual Approach – Using a Diagram
The easiest way to grasp dividing 3/4 cup in half is through a visual representation. Imagine a measuring cup divided into four equal parts. Shade three of those parts to represent 3/4. Now, divide those three shaded parts into two equal groups. Each group will represent half of 3/4. You'll find that each group contains one and a half of the original four parts. Therefore, half of 3/4 cup is 3/8 cup.
Method 2: The Mathematical Approach – Fraction Multiplication
Dividing by 2 is the same as multiplying by 1/2. Therefore, to find half of 3/4, we multiply 3/4 by 1/2:
(3/4) * (1/2) = (3 * 1) / (4 * 2) = 3/8
This confirms our visual approach: half of 3/4 cup is 3/8 cup.
Method 3: Converting to Decimals – A Numerical Approach
Another way to approach this problem is by converting the fraction to a decimal. 3/4 is equal to 0.75. Dividing 0.75 by 2 gives us 0.375. To convert this back into a fraction, we can recognize that 0.375 is equivalent to 375/1000. Simplifying this fraction by dividing both numerator and denominator by 125 gives us 3/8. Again, we arrive at the same answer: 3/8 cup.
Extending the Concept: Dividing Other Fractions
The principles we've used to divide 3/4 cup in half can be applied to dividing other fractions. The general rule for dividing fractions is to multiply the first fraction by the reciprocal of the second fraction. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2 is 1/2, and the reciprocal of 3/4 is 4/3.
Let’s consider a few examples:
- Dividing 1/2 by 1/4: (1/2) / (1/4) = (1/2) * (4/1) = 4/2 = 2
- Dividing 2/3 by 1/6: (2/3) / (1/6) = (2/3) * (6/1) = 12/3 = 4
- Dividing 5/8 by 3/4: (5/8) / (3/4) = (5/8) * (4/3) = 20/24 = 5/6
Practical Applications Beyond the Kitchen
While dividing fractions often pops up in cooking and baking recipes, its applications are far broader. Consider these examples:
- Sewing and Crafting: Calculating fabric requirements, dividing patterns, or adjusting project sizes often involves fractions.
- Construction and Carpentry: Precise measurements are crucial in these fields, requiring frequent fraction calculations.
- Financial Management: Dividing budgets, calculating percentages, and understanding fractional shares in investments all involve fraction manipulation.
- Data Analysis: Understanding data often involves representing it using fractions and percentages, requiring division of fractions.
Common Mistakes to Avoid
When working with fractions, some common mistakes can lead to incorrect results. Here are a few to watch out for:
- Confusing multiplication with division: Remember that dividing by a number is equivalent to multiplying by its reciprocal.
- Not simplifying fractions: Always simplify your fractions to their lowest terms for the clearest and most concise answer.
- Incorrectly applying the order of operations: If your calculation involves multiple operations, remember to follow the order of operations (PEMDAS/BODMAS).
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to divide fractions? A: Yes, many calculators have a fraction function that can handle fraction division directly. You can also convert the fractions to decimals before dividing.
-
Q: What if I need to divide 3/4 cup into more than two parts? A: Follow the same principles. For example, to divide 3/4 cup into three equal parts, you would multiply 3/4 by 1/3: (3/4) * (1/3) = 1/4 cup per part.
-
Q: What if I don't have a measuring cup with markings for 3/8 cup? A: You can use a smaller measuring spoon or estimate 3/8 cup by visually dividing the 3/4 cup portion already measured into two equal parts.
Conclusion: Mastering Fraction Division
Dividing 3/4 cup in half, seemingly a trivial task, provides a gateway to understanding fundamental concepts of fraction division. By employing visual, mathematical, or decimal approaches, we consistently arrive at the answer: 3/8 cup. This understanding extends beyond simple cooking measurements, proving invaluable across diverse fields demanding accurate and efficient calculations. By mastering these principles, you’ll enhance your problem-solving skills and confidently tackle even more complex fraction-related challenges in your daily life and endeavors. Remember to practice regularly, utilize various methods, and always double-check your work to ensure accuracy. With dedication and consistent practice, conquering the world of fractions will become second nature.
Latest Posts
Latest Posts
-
Hypotenuse Formula For Right Triangle
Sep 17, 2025
-
Why Are Cookies Called Cookies
Sep 17, 2025
-
Protons Neutrons Electrons Of Carbon
Sep 17, 2025
-
How To Get Marginal Revenue
Sep 17, 2025
-
1 Tbsp Peanut Butter Nutrition
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Cup Divided In Half . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.