Integral Of 1 3 X
straightsci
Sep 12, 2025 · 5 min read
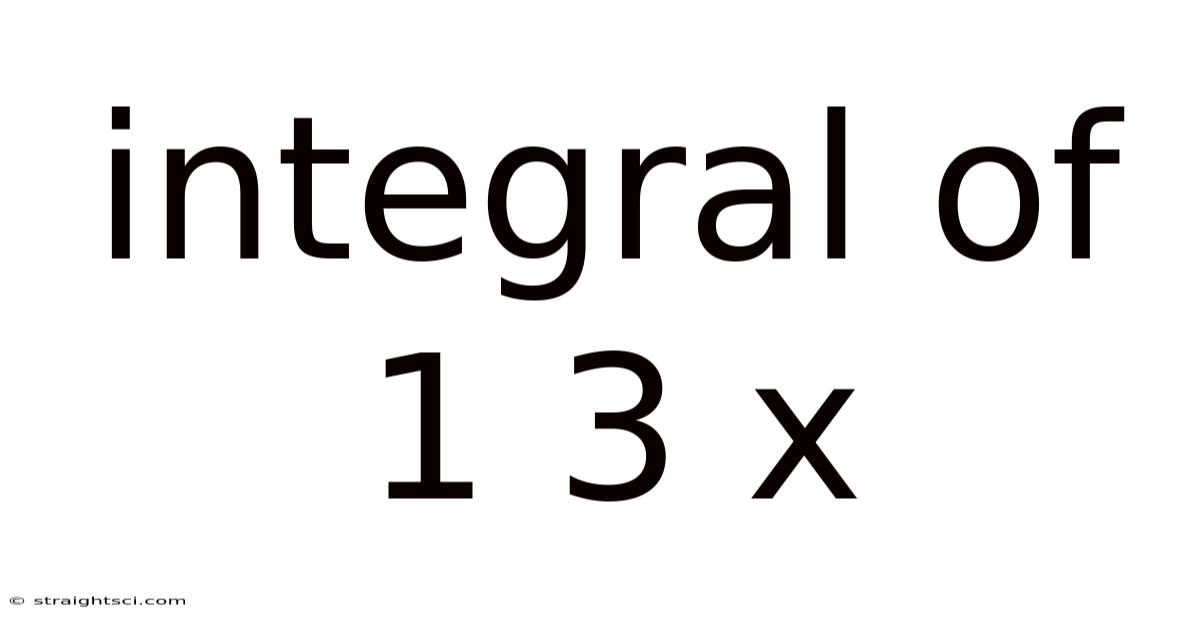
Table of Contents
Understanding and Solving the Integral of 1/(3x)
The integral of 1/(3x) is a fundamental concept in calculus, representing the inverse process of differentiation. This seemingly simple integral introduces key ideas about integration techniques, particularly involving logarithmic functions. This article will comprehensively explore this integral, providing step-by-step solutions, detailed explanations, and addressing common misconceptions. We'll delve into the underlying mathematical principles and offer practical applications to solidify your understanding.
Introduction: Navigating the World of Integrals
In calculus, integration is the process of finding a function whose derivative is a given function. This "antiderivative" is represented by the integral symbol ∫. The integral we're focusing on, ∫(1/(3x)) dx, involves a rational function – a ratio of two polynomials. Understanding how to solve this integral is crucial for mastering more complex integration problems.
The presence of 'x' in the denominator immediately suggests that the solution will likely involve a logarithmic function, as the derivative of a logarithmic function contains a reciprocal. Let's dive into the solution process.
Step-by-Step Solution: Unraveling the Integral
The key to solving ∫(1/(3x)) dx lies in recognizing and applying the appropriate integration rules. We'll break down the solution into manageable steps:
Step 1: Constant Factor Rule
The constant factor rule states that the integral of a constant times a function is equal to the constant times the integral of the function. In our case, we can pull the constant 1/3 out of the integral:
∫(1/(3x)) dx = (1/3) ∫(1/x) dx
Step 2: Integral of 1/x
The integral of 1/x is a standard integral that results in the natural logarithm of the absolute value of x:
∫(1/x) dx = ln|x| + C
Here, 'C' represents the constant of integration. This constant is essential because the derivative of a constant is always zero; therefore, infinitely many functions can have the same derivative.
Step 3: Combining the Results
Substituting the result from Step 2 back into the equation from Step 1, we obtain the final solution:
(1/3) ∫(1/x) dx = (1/3) ln|x| + C
Therefore, the integral of 1/(3x) is (1/3)ln|x| + C.
The Importance of the Absolute Value: A Crucial Detail
The absolute value, |x|, is crucial in the final answer, ln|x|. The natural logarithm function, ln(x), is only defined for positive values of x. By using the absolute value, we ensure that the function is defined for both positive and negative values of x. The derivative of ln|x| is still 1/x, regardless of the sign of x.
Visualizing the Solution: A Graphical Perspective
It’s helpful to visualize the solution graphically. The function f(x) = 1/(3x) is a hyperbola. Its integral, F(x) = (1/3)ln|x| + C, represents a family of curves (each curve corresponding to a different value of C), each representing the area under the curve of f(x) from a given point to x. The constant of integration 'C' dictates the vertical shift of this family of curves.
The Scientific Significance: Applications of the Integral
The integral of 1/(3x) finds applications in various scientific fields, including:
- Physics: Calculating work done by a variable force. If a force is inversely proportional to distance (like in certain gravitational fields), this integral appears in the calculation of work.
- Chemistry: Determining reaction rates in certain chemical processes where the rate depends inversely on the concentration of a reactant.
- Economics: Modeling situations where a rate of change is inversely proportional to a quantity (e.g., changes in market price).
- Engineering: Solving differential equations that describe physical systems where the rate of change of a quantity is proportional to its reciprocal.
Expanding the Concept: More Complex Integrals
While this article focuses on the integral of 1/(3x), understanding this fundamental integral lays the groundwork for tackling more complex integrals involving similar rational functions. Techniques like u-substitution can often simplify these more complex scenarios. For example, consider the integral:
∫ (1/(3x + 2)) dx
This can be solved using u-substitution, where u = 3x + 2. This leads to a similar integral form, which can be solved using the same logarithmic approach.
Frequently Asked Questions (FAQ)
Q1: What is the constant of integration 'C', and why is it important?
A1: The constant of integration 'C' accounts for the fact that the derivative of a constant is zero. Therefore, many functions can have the same derivative. The constant 'C' represents the vertical shift of the family of curves representing the integral. It's essential for representing the general solution, not just a particular solution.
Q2: Can I solve this integral using a different method?
A2: While the method described above is the most straightforward, you could potentially use techniques like integration by parts, but it would be considerably more complex and less efficient for this specific integral.
Q3: What happens if x is zero?
A3: The function 1/(3x) is undefined at x = 0. The integral is only defined for intervals where x is not equal to zero.
Q4: How does the absolute value affect the interpretation of the integral?
A4: The absolute value ensures the logarithm is defined for both positive and negative x values. This maintains the continuity of the antiderivative. Without the absolute value, the domain of the integral would be restricted to only positive x values.
Conclusion: Mastering Fundamental Concepts in Calculus
Understanding the integral of 1/(3x) is a significant step in mastering calculus. This seemingly simple integral highlights the importance of fundamental integration rules, the crucial role of the constant of integration, and the careful consideration of the domain of the function. By grasping these concepts, you'll be well-equipped to tackle more complex integration problems and apply these principles to various scientific and engineering disciplines. Remember, the key is to practice consistently and build a solid foundation in the fundamental rules of integration. Through consistent effort and a deeper understanding of these principles, you’ll find that the complexities of calculus begin to unravel into a beautiful and logical system.
Latest Posts
Latest Posts
-
Great Barrier Reef In Space
Sep 12, 2025
-
Hemingway Six Word Short Story
Sep 12, 2025
-
Electron Configuration For O 2
Sep 12, 2025
-
What Does Ram Stand For
Sep 12, 2025
-
How To Find Mean Deviation
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 3 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.