Factor 2x 2 5x 3
straightsci
Sep 15, 2025 · 6 min read
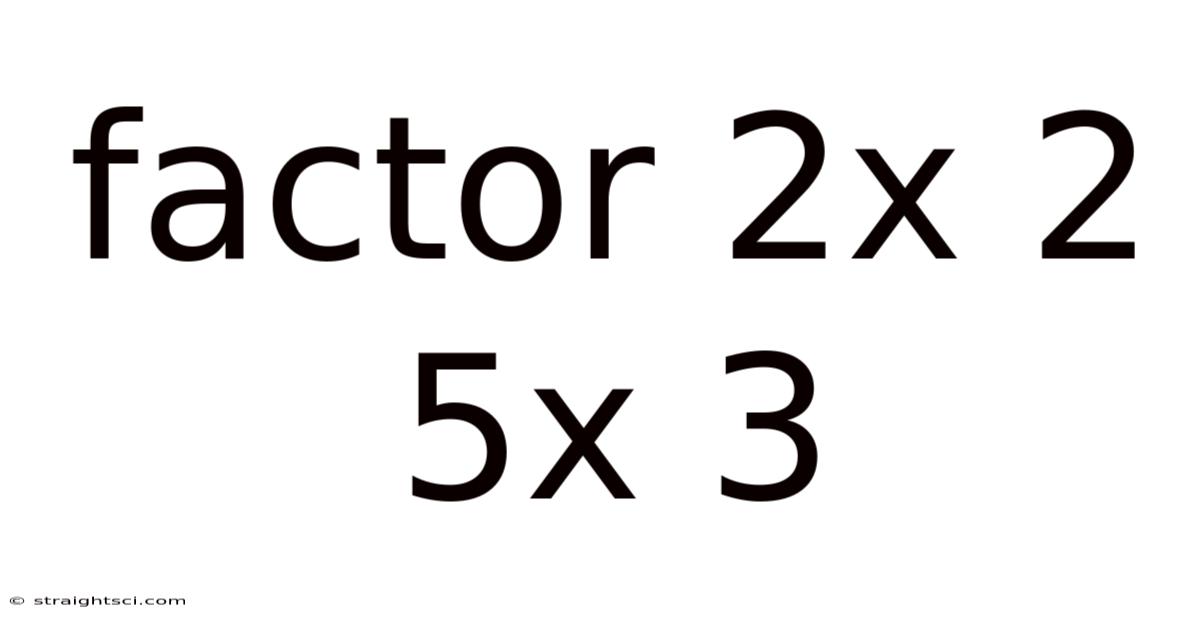
Table of Contents
Factoring Quadratic Expressions: A Deep Dive into 2x² + 5x + 3
Factoring quadratic expressions is a fundamental skill in algebra, crucial for solving equations, simplifying expressions, and understanding more advanced mathematical concepts. This comprehensive guide will walk you through the process of factoring the specific quadratic expression 2x² + 5x + 3, and then extend this knowledge to help you tackle other similar problems. We’ll explore various methods, provide detailed explanations, and address common questions. Mastering this skill will significantly enhance your algebraic proficiency.
Understanding Quadratic Expressions
Before diving into the factoring process, let's establish a solid understanding of what a quadratic expression is. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually 'x') is 2. It generally takes the form ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. In our case, the quadratic expression is 2x² + 5x + 3, where a = 2, b = 5, and c = 3.
Method 1: Factoring by Grouping (AC Method)
This method is particularly useful when the coefficient of x² (the 'a' value) is greater than 1. Here's how it works for 2x² + 5x + 3:
-
Find the product 'ac': Multiply the coefficient of x² (a = 2) and the constant term (c = 3). This gives us ac = 2 * 3 = 6.
-
Find two numbers that add up to 'b' and multiply to 'ac': We need two numbers that add up to 5 (the coefficient of x, which is 'b') and multiply to 6. These numbers are 2 and 3 (2 + 3 = 5 and 2 * 3 = 6).
-
Rewrite the middle term: Rewrite the middle term (5x) as the sum of the two numbers we found in step 2, using x as the variable: 5x = 2x + 3x.
-
Group the terms: Group the four terms into two pairs: (2x² + 2x) + (3x + 3).
-
Factor out the greatest common factor (GCF) from each pair:
- From (2x² + 2x), the GCF is 2x. Factoring it out gives 2x(x + 1).
- From (3x + 3), the GCF is 3. Factoring it out gives 3(x + 1).
-
Factor out the common binomial factor: Notice that both terms now share the common binomial factor (x + 1). Factor this out: (x + 1)(2x + 3).
Therefore, the factored form of 2x² + 5x + 3 is (x + 1)(2x + 3).
Method 2: Trial and Error
This method involves systematically testing different binomial pairs until you find the correct combination. It's often faster for simpler quadratics, but can be time-consuming for more complex ones.
-
Set up the binomial factors: Since the coefficient of x² is 2, the first terms in the binomial factors must be 2x and x: (2x )(x ).
-
Consider the factors of the constant term: The constant term is 3, which has only two factors: 1 and 3.
-
Test different combinations: We need to place 1 and 3 in the second positions of the binomials in a way that when we expand the expression using the FOIL (First, Outer, Inner, Last) method, we get the original quadratic:
- (2x + 1)(x + 3): Expanding this gives 2x² + 7x + 3 (incorrect).
- (2x + 3)(x + 1): Expanding this gives 2x² + 5x + 3 (correct!).
Therefore, the factored form, using the trial and error method, is again (2x + 3)(x + 1). Note that the order of the factors doesn't matter since multiplication is commutative.
Checking Your Answer
It's always a good idea to check your factored answer by expanding it using the FOIL method:
(2x + 3)(x + 1) = 2x² + 2x + 3x + 3 = 2x² + 5x + 3
This confirms that our factoring is correct.
Expanding the Concept: Factoring Other Quadratics
The methods described above are applicable to a wide range of quadratic expressions. Let's consider some examples:
-
x² + 5x + 6: Using either method, this factors to (x + 2)(x + 3). Notice here that 'a' = 1, making the factoring process slightly simpler.
-
3x² - 7x + 2: Using the factoring by grouping method, ac = 6. The two numbers that add to -7 and multiply to 6 are -1 and -6. This factors to (3x - 1)(x - 2).
-
x² - 4: This is a special case called the difference of squares. It factors to (x - 2)(x + 2).
-
4x² + 12x + 9: This is a perfect square trinomial, and it factors to (2x + 3)².
Dealing with Negative Coefficients
When dealing with negative coefficients in your quadratic expression, remember that the signs of the factors are crucial. For example:
- 2x² - 5x + 3: Using the factoring by grouping method, ac = 6. The two numbers that add to -5 and multiply to 6 are -2 and -3. This factors to (2x - 3)(x - 1).
When Factoring is Not Possible (Prime Quadratics)
Not all quadratic expressions can be factored neatly using integer coefficients. These are often referred to as prime quadratics. For example, x² + x + 1 cannot be factored using integers. In such cases, more advanced techniques like the quadratic formula are necessary to find the roots (or solutions) of the corresponding quadratic equation.
Applications of Factoring Quadratic Expressions
Factoring quadratic expressions has numerous applications in various areas of mathematics and beyond:
-
Solving Quadratic Equations: Setting a quadratic expression equal to zero creates a quadratic equation. Factoring allows you to find the solutions (roots) of the equation by setting each factor to zero and solving for x.
-
Simplifying Rational Expressions: Factoring is essential for simplifying rational expressions (fractions with polynomials in the numerator and denominator) by canceling common factors.
-
Graphing Parabolas: The factored form of a quadratic expression provides valuable information about the parabola's x-intercepts (where the graph crosses the x-axis).
-
Calculus: Factoring plays a key role in techniques like finding derivatives and integrals.
Frequently Asked Questions (FAQ)
Q: What if I can't find the factors easily?
A: If you're struggling to find the two numbers that add up to 'b' and multiply to 'ac', you can always use the quadratic formula to find the roots of the corresponding quadratic equation. The roots will help you determine the factors.
Q: Is there a specific order to the factors?
A: No, the order of the factors doesn't matter due to the commutative property of multiplication. (x + 1)(2x + 3) is the same as (2x + 3)(x + 1).
Q: What if the quadratic expression has a common factor?
A: Always look for a greatest common factor (GCF) among all the terms before attempting to factor the quadratic. For example, in 6x² + 12x + 6, the GCF is 6, so you would first factor out the 6: 6(x² + 2x + 1), and then factor the remaining quadratic (x² + 2x + 1) to (x + 1)². The fully factored expression is 6(x + 1)².
Q: How can I practice my factoring skills?
A: Practice is key! Work through numerous examples, varying the coefficients and signs. Use online resources, textbooks, and practice problems to hone your skills.
Conclusion
Factoring quadratic expressions, like 2x² + 5x + 3, is a cornerstone of algebra. Understanding the underlying principles and mastering both the factoring by grouping and trial and error methods will significantly boost your problem-solving abilities in algebra and beyond. Remember to check your answers and practice regularly to solidify your understanding. With consistent effort, you'll become proficient in factoring and confident in tackling more complex algebraic problems. The key is to understand the underlying principles, practice consistently, and don't be afraid to seek help when needed. Good luck!
Latest Posts
Latest Posts
-
Boiling Temperature Of Isopropyl Alcohol
Sep 15, 2025
-
What Is 1 88m In Feet
Sep 15, 2025
-
How To Determine The Hypotenuse
Sep 15, 2025
-
15 Oz How Many Ml
Sep 15, 2025
-
What Is 8oz In Ml
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Factor 2x 2 5x 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.