6 X 9 X 2
straightsci
Sep 13, 2025 · 6 min read
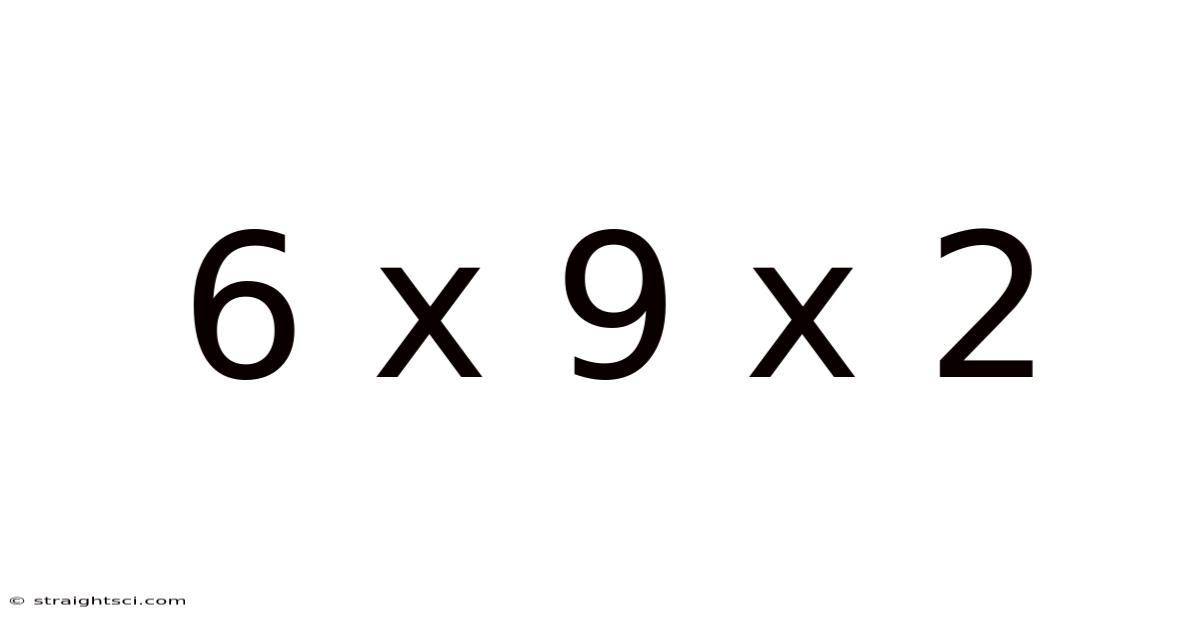
Table of Contents
Decoding 6 x 9 x 2: Exploring Dimensions, Volume, and Practical Applications
This article delves into the seemingly simple dimensions "6 x 9 x 2," exploring their mathematical implications, practical applications across various fields, and the significance of understanding spatial relationships. We'll move beyond the basic calculations to uncover the broader context of how such dimensions are used in design, engineering, packaging, and even everyday life. Understanding these dimensions is fundamental to grasping concepts in geometry, measurement, and spatial reasoning.
Understanding the Dimensions: 6 x 9 x 2
The notation "6 x 9 x 2" represents three perpendicular measurements, typically interpreted as length, width, and height (or depth). In this case:
- 6: Represents the length (or longest side) of a three-dimensional object.
- 9: Represents the width (or the side perpendicular to the length).
- 2: Represents the height (or depth, the side perpendicular to both length and width).
These measurements are usually expressed in the same unit (e.g., inches, centimeters, feet). Without specifying the unit, we can only deal with the relative proportions. The understanding of units is crucial for practical applications.
Calculating the Volume: A Simple Cubic Measurement
One of the most immediate calculations we can perform with these dimensions is determining the volume of the object. The volume of a rectangular prism (a box-shaped object) is calculated by multiplying length, width, and height:
Volume = Length x Width x Height = 6 x 9 x 2 = 108 cubic units
Again, the "cubic units" depend on the unit used for the original dimensions. If the dimensions are in centimeters, the volume is 108 cubic centimeters (cm³). If the dimensions are in inches, the volume is 108 cubic inches (in³). This calculation forms the basis for many practical applications, from calculating the capacity of containers to estimating material quantities.
Practical Applications Across Diverse Fields
The dimensions 6 x 9 x 2, or variations thereof, appear in numerous contexts. Let's explore some examples:
1. Packaging and Shipping:
-
Boxes: Many products are packaged in boxes with dimensions approximating 6 x 9 x 2 (or scaled versions). This size might be ideal for smaller items, books, or specialized goods. Optimizing package dimensions is key for efficient shipping and minimizing wasted space. Understanding the volume allows for efficient packing and calculating shipping costs.
-
Envelopes: While not precisely 6 x 9 x 2, the dimensions are relevant to the sizing of larger envelopes. The principles of maximizing space and optimizing dimensions are applicable here as well. Designers consider these factors when creating standard envelope sizes.
2. Construction and Engineering:
-
Bricks and Blocks: Construction materials often come in standard sizes. While not exactly 6 x 9 x 2, the dimensions relate to the general idea of creating standardized units for easy construction and calculation. Understanding the volume of these units is critical for estimating materials needed for a project.
-
Modular Design: Many structures use modular designs, incorporating repetitive units of similar dimensions. This simplifies construction, reduces errors, and streamlines the process. The dimensions 6 x 9 x 2 could represent a basic module in various applications.
3. Manufacturing and Production:
-
Component Sizing: In manufacturing, components often need to fit within specific spaces. The dimensions 6 x 9 x 2 might dictate the size of a part or the internal dimensions of a housing. Precise measurements are crucial for proper functionality and assembly.
-
Inventory Management: Knowing the dimensions of items helps in optimizing warehouse space and improving inventory management. Accurate calculations of volume and space are essential for efficient logistics.
4. Everyday Life:
-
Storage Containers: Household storage containers often come in various sizes. A container with dimensions around 6 x 9 x 2 could be useful for storing a range of items. Choosing the right size container maximizes space efficiency.
-
Furniture Design: The dimensions influence the design of small furniture pieces. Side tables, small shelves, or other compact furniture could be designed with dimensions related to 6 x 9 x 2.
Scaling and Proportionality: The Significance of Ratios
While we've focused on the specific dimensions 6 x 9 x 2, it's important to understand the principles of scaling and proportionality. A similar-shaped object with dimensions 12 x 18 x 4 (double the original dimensions in all directions) would have a volume eight times larger (2³ = 8). This relationship is critical in design and engineering, allowing for the creation of scaled models or larger versions of a design.
Beyond the Numbers: Visualizing and Understanding Space
Beyond the mathematical calculations, it's crucial to develop a spatial understanding of the dimensions 6 x 9 x 2. Visualizing this as a rectangular prism is essential for applying these dimensions in practical contexts. This visualization skill is important in various fields, from architecture and design to packing and logistics.
Mathematical Extensions and Related Concepts
The dimensions 6 x 9 x 2 open doors to various mathematical concepts:
-
Surface Area: Calculating the surface area of the rectangular prism (sum of the areas of all six faces) requires understanding the relationship between dimensions and area. This is crucial in material estimation and cost calculations.
-
Geometry: The rectangular prism itself is a foundational concept in geometry. Understanding its properties, including volume, surface area, and diagonals, is fundamental to spatial reasoning.
-
Coordinate Systems: The dimensions can be represented in a three-dimensional coordinate system, further solidifying the spatial understanding.
Frequently Asked Questions (FAQ)
Q1: What happens if I change the order of the numbers (e.g., 9 x 2 x 6)?
A1: The volume remains the same because multiplication is commutative (the order doesn't change the result). However, the orientation of the object changes. It will still be a rectangular prism, but its dimensions will be oriented differently.
Q2: What units are commonly used with these dimensions?
A2: Common units include inches, centimeters, feet, and meters. The choice of unit depends on the context of application. For small objects, inches or centimeters might be used. For larger objects, feet or meters would be more appropriate.
Q3: How can I visualize these dimensions?
A3: Try using a physical object as a reference. Imagine a shoebox or a small rectangular container. You can even draw a diagram to represent the length, width, and height, creating a three-dimensional sketch.
Conclusion: The Power of Understanding Dimensions
The seemingly simple dimensions 6 x 9 x 2 represent more than just numbers. They encapsulate fundamental principles of measurement, geometry, and spatial reasoning. Understanding these principles, from calculating volume to visualizing three-dimensional shapes, is crucial for success in a wide range of fields. Whether you're designing a product, constructing a building, or simply organizing your closet, grasping the implications of such dimensions is a valuable skill. The application of these concepts extends far beyond simple calculations, highlighting the importance of spatial understanding and mathematical literacy in our daily lives. By mastering these foundational concepts, you open the door to more advanced studies in geometry, engineering, and design.
Latest Posts
Latest Posts
-
Four Types Of Reactions Chemistry
Sep 13, 2025
-
Anatomy Pelvic Floor Muscles Female
Sep 13, 2025
-
5 5 Ft In Inches
Sep 13, 2025
-
Is Symbolism A Literary Technique
Sep 13, 2025
-
Formula For Perimeter Of Square
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 6 X 9 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.