Cos2x Cos 2x Sin 2x
straightsci
Sep 19, 2025 · 6 min read
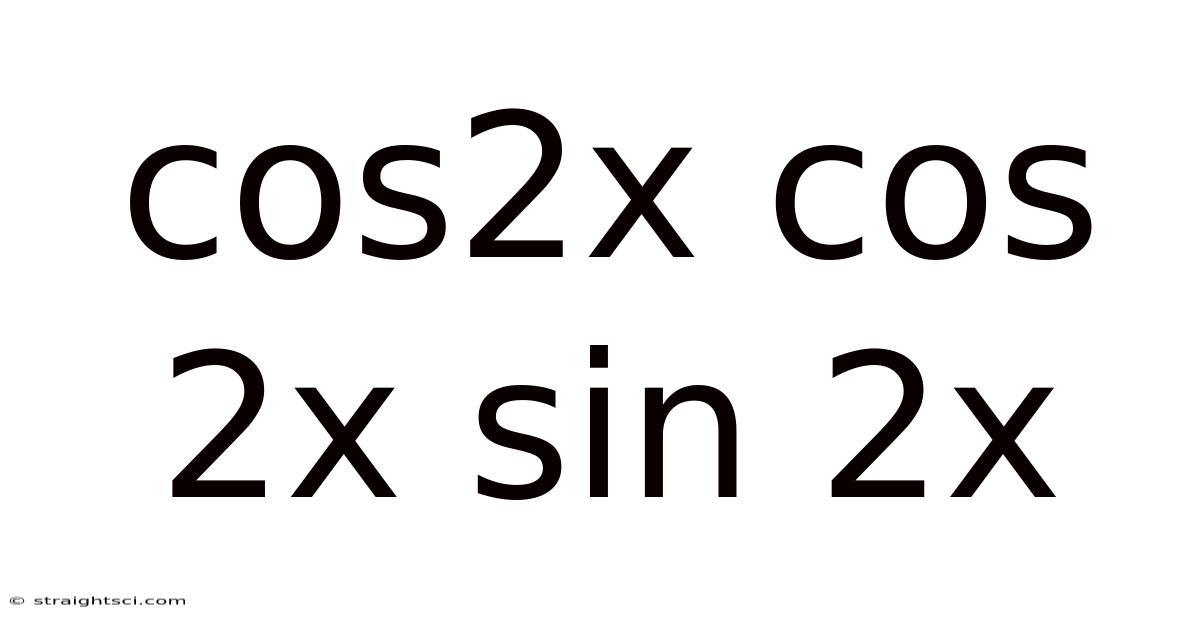
Table of Contents
Mastering Trigonometric Identities: A Deep Dive into cos²2x, cos2x, and sin2x
Understanding trigonometric identities is crucial for success in mathematics, particularly in calculus, physics, and engineering. This article provides a comprehensive exploration of the trigonometric expressions cos²2x, cos2x, and sin2x, examining their relationships, derivations, and applications. We'll delve into the fundamental identities, explore how to manipulate them, and address common misconceptions. By the end, you'll possess a solid grasp of these functions and be equipped to solve a wide range of trigonometric problems.
Introduction: The Building Blocks of Trigonometry
Trigonometry, at its core, deals with the relationships between angles and sides of triangles. However, its applications extend far beyond basic geometry. The functions sine (sin), cosine (cos), and tangent (tan), along with their reciprocal functions (cosecant, secant, and cotangent), form the foundation of trigonometric analysis. Understanding their properties and how they interact is essential. This article focuses on the double-angle versions of these functions, specifically cos²2x, cos2x, and sin2x, showing how they relate to each other and how to work with them effectively.
Understanding Double-Angle Identities
The expressions cos²2x, cos2x, and sin2x involve the concept of double angles. A double angle represents an angle that is twice the measure of another angle. For instance, if x = 30°, then 2x = 60°. The double-angle identities provide formulas that express trigonometric functions of a double angle in terms of trigonometric functions of the single angle. These identities are derived from the sum-to-product formulas and are incredibly useful for simplifying complex trigonometric expressions and solving trigonometric equations.
Here are the key double-angle identities:
-
sin2x = 2sin x cos x: This identity expresses the sine of a double angle as twice the product of the sine and cosine of the single angle.
-
cos2x: The cosine of a double angle has several equivalent forms:
- cos2x = cos²x - sin²x: This is a direct derivation from the cosine sum formula.
- cos2x = 2cos²x - 1: This form is obtained by substituting sin²x = 1 - cos²x into the previous equation.
- cos2x = 1 - 2sin²x: This form is obtained by substituting cos²x = 1 - sin²x into the first form.
-
cos²2x: This represents the square of the cosine of a double angle. It can be expressed using the various forms of cos2x:
- cos²2x = (cos²x - sin²x)²
- cos²2x = (2cos²x - 1)²
- cos²2x = (1 - 2sin²x)²
Deriving the Double-Angle Identities
Let's illustrate the derivation of one of the key identities: sin2x = 2sin x cos x. We'll utilize the angle sum formula for sine:
sin(A + B) = sin A cos B + cos A sin B
Let A = x and B = x. Then:
sin(x + x) = sin x cos x + cos x sin x
sin2x = 2sin x cos x
Similar derivations, using the angle sum formula for cosine, can be used to obtain the different forms of the cos2x identity. These derivations rely on fundamental trigonometric identities such as the Pythagorean identity (sin²x + cos²x = 1).
Applications of cos²2x, cos2x, and sin2x
These identities find extensive use in various mathematical and scientific applications:
-
Simplifying Trigonometric Expressions: The double-angle identities are indispensable tools for simplifying complex trigonometric expressions. They allow us to reduce the complexity of expressions involving multiple angles, making them easier to manipulate and solve.
-
Solving Trigonometric Equations: Many trigonometric equations can be efficiently solved by using the double-angle identities to rewrite the equation in a simpler form. This often involves substituting the double-angle identities to create a quadratic equation in terms of sin x or cos x, which can then be solved using standard algebraic techniques.
-
Calculus: In calculus, these identities play a crucial role in integration and differentiation of trigonometric functions. They are frequently used to simplify integrands or to express derivatives in a more manageable form. For example, they are essential for solving integrals involving powers of sine and cosine.
-
Physics and Engineering: These identities frequently appear in physics and engineering problems involving oscillatory motion, wave phenomena, and alternating currents. The periodic nature of trigonometric functions, and the ability to manipulate these functions using identities, makes them vital for modeling and analyzing these systems.
Working with the Identities: Examples
Let's work through a few examples to illustrate the practical application of these identities:
Example 1: Simplifying an Expression
Simplify the expression: sin4x
Using the double-angle identity for sine, we can rewrite sin4x as sin(2(2x)):
sin4x = 2sin2x cos2x
Now, we can apply the double-angle identities again:
sin4x = 2(2sin x cos x)(cos²x - sin²x)
sin4x = 4sin x cos x (cos²x - sin²x)
This demonstrates how the double-angle identities allow us to express a trigonometric function of a multiple angle in terms of functions of a single angle.
Example 2: Solving a Trigonometric Equation
Solve the equation: cos2x = sin x
Using the identity cos2x = 1 - 2sin²x, we substitute:
1 - 2sin²x = sin x
Rearranging into a quadratic equation:
2sin²x + sin x - 1 = 0
Factoring the quadratic:
(2sin x - 1)(sin x + 1) = 0
This gives two solutions:
2sin x - 1 = 0 => sin x = 1/2 => x = π/6, 5π/6,... sin x + 1 = 0 => sin x = -1 => x = 3π/2,...
This example highlights how the double-angle identities can transform a seemingly complex trigonometric equation into a solvable algebraic equation.
Common Mistakes and Misconceptions
-
Incorrect Application of Identities: A common mistake is incorrectly applying the identities or misinterpreting the formulas. Always double-check your work and ensure you are correctly substituting values and using the appropriate identity.
-
Confusing Double-Angle and Half-Angle Identities: Remember to distinguish between double-angle identities and half-angle identities. These are distinct sets of formulas with different applications.
-
Overlooking the General Solution: When solving trigonometric equations, remember to find the general solution, which encompasses all possible solutions within a given range. The solutions found are often just a subset of the full solution set.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between cos2x and cos²2x?
- A: cos2x represents the cosine of a double angle, while cos²2x represents the square of the cosine of a double angle. They are distinct mathematical expressions.
-
Q: Can I use these identities for any angle x?
- A: Yes, these identities hold true for any angle x, provided the trigonometric functions are defined for that angle.
-
Q: Are there triple-angle identities?
- A: Yes, there are triple-angle identities and, in fact, multiple-angle identities for higher multiples. These are derived using iterative applications of the double-angle and sum-to-product formulas.
-
Q: How do I choose which form of the cos2x identity to use?
- A: The best form to use depends on the specific problem. If the problem already contains sin²x or cos²x, it's usually most efficient to choose the form that involves that particular term. Sometimes you may have to try different forms to find the most efficient route to a solution.
Conclusion: Mastering the Power of Trigonometric Identities
Understanding and mastering trigonometric identities, particularly the double-angle identities for cos²2x, cos2x, and sin2x, is fundamental to success in many areas of mathematics, science, and engineering. By understanding their derivations, applications, and potential pitfalls, you'll gain a powerful toolset to simplify complex expressions, solve challenging equations, and effectively analyze a vast range of problems involving periodic functions and oscillatory systems. Practice is key – the more you work with these identities, the more intuitive and effective their use will become. Remember to carefully check your work and consider the broader context of the problem to choose the most efficient approach.
Latest Posts
Latest Posts
-
Armature Of An Electric Motor
Sep 19, 2025
-
Vm Virtualbox Exit Full Screen
Sep 19, 2025
-
How Far Is 1000 Ft
Sep 19, 2025
-
5 6 As A Percent
Sep 19, 2025
-
Formula From Centigrade To Fahrenheit
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Cos2x Cos 2x Sin 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.