5 1/8 In Decimal Form
straightsci
Sep 08, 2025 · 6 min read
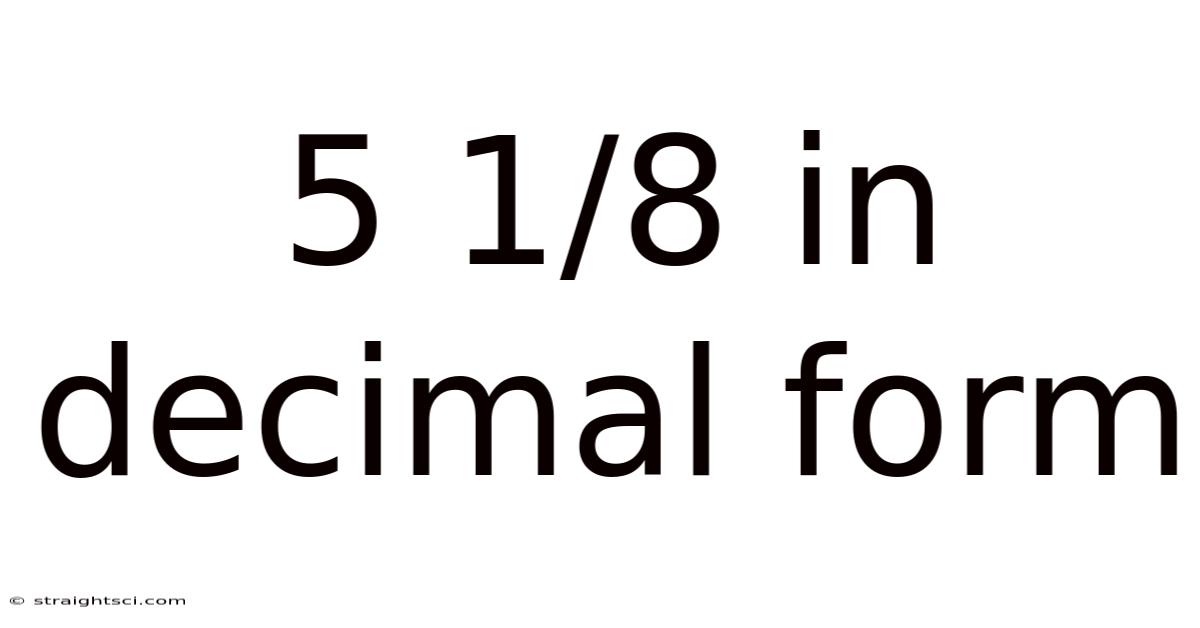
Table of Contents
5 1/8 in Decimal Form: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will delve into the conversion of the mixed number 5 1/8 into its decimal equivalent, exploring the process step-by-step and providing a deeper understanding of the underlying principles. We will cover different methods, address common misconceptions, and even touch upon the practical applications of such conversions. By the end, you'll not only know the decimal form of 5 1/8 but also possess a solid grasp of fraction-to-decimal conversion techniques.
Understanding Mixed Numbers and Fractions
Before we embark on the conversion process, let's clarify the terminology. A mixed number combines a whole number and a fraction, like 5 1/8. This signifies five whole units plus one-eighth of another unit. A fraction, on the other hand, represents a part of a whole. In 5 1/8, 1 is the numerator (the top number) and 8 is the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts we are considering.
Method 1: Converting the Fraction to a Decimal, Then Adding the Whole Number
This is arguably the most straightforward approach for converting a mixed number like 5 1/8 to its decimal equivalent. We break the process into two manageable steps:
-
Convert the fraction to a decimal: To convert the fraction 1/8 to a decimal, we perform the division: 1 ÷ 8. This gives us 0.125.
-
Add the whole number: Now, we simply add the whole number part (5) to the decimal equivalent of the fraction (0.125): 5 + 0.125 = 5.125
Therefore, 5 1/8 in decimal form is 5.125.
Method 2: Converting the Entire Mixed Number to an Improper Fraction, Then to a Decimal
This method involves an extra step but provides a deeper understanding of fraction manipulation. It's particularly helpful when dealing with more complex mixed numbers.
-
Convert to an improper fraction: An improper fraction has a numerator larger than or equal to its denominator. To convert 5 1/8 to an improper fraction, we first multiply the whole number (5) by the denominator (8): 5 x 8 = 40. Then, we add the numerator (1): 40 + 1 = 41. This becomes the new numerator, while the denominator remains the same (8). Therefore, the improper fraction is 41/8.
-
Convert the improper fraction to a decimal: Now, we divide the numerator (41) by the denominator (8): 41 ÷ 8 = 5.125
Again, we arrive at the same result: 5 1/8 is equal to 5.125 in decimal form.
Method 3: Using Long Division (for a deeper understanding)
While the previous methods are efficient, understanding long division provides a more fundamental grasp of the conversion process. This method directly converts the mixed number into a decimal without the intermediary step of converting to an improper fraction.
-
Set up the long division: We set up the long division problem as 5 1/8, which means we are dividing 5.125 (obtained from the previous method) by 1.
-
Perform the long division: The long division process would look like this:
5.125 8 | 41.000 40 ---- 10 8 -- 20 16 --- 40 40 -- 0We start by dividing 41 by 8. We get 5 with a remainder of 1. We add a decimal point and a zero to continue the division, and the process is repeated until we reach a remainder of 0 or a repeating pattern. This yields the decimal value of 5.125.
Understanding Decimal Place Value
The decimal number 5.125 comprises several place values:
- 5: Represents the whole number part (ones place).
- 1: Represents one-tenth (tenths place).
- 2: Represents two-hundredths (hundredths place).
- 5: Represents five-thousandths (thousandths place).
Understanding place value helps in interpreting and manipulating decimal numbers accurately.
Practical Applications of Decimal Conversions
The ability to convert fractions to decimals is essential in many real-world applications:
-
Measurements: Many measurement systems use both fractions (e.g., inches) and decimals (e.g., metric system). Converting between them is necessary for accurate calculations and conversions. For example, in carpentry, understanding 5 1/8 inches as 5.125 inches is crucial for precise measurements.
-
Finance: Financial calculations often involve fractions (e.g., shares of stock). Converting these fractions to decimals allows for easier calculations of profits, losses, and interest.
-
Science and Engineering: Scientific and engineering applications frequently use decimal numbers for calculations involving precision and accuracy. Converting fractions to decimals ensures consistency and facilitates calculations.
-
Data Analysis: Data analysis often requires converting fractional data into decimal format for computation and easier interpretation using statistical software.
-
Computer Programming: Many programming languages require numerical data to be in decimal form for calculations and data manipulation.
Frequently Asked Questions (FAQ)
-
Q: Can all fractions be converted to terminating decimals?
- A: No, fractions with denominators that have prime factors other than 2 and 5 will result in repeating decimals (e.g., 1/3 = 0.333...). 1/8, however, has a denominator (8 = 2³) composed only of the prime factor 2, so it results in a terminating decimal.
-
Q: What if I have a larger mixed number? Will the process be the same?
- A: Yes, the process remains the same. Simply convert the fractional part to a decimal using division and then add the whole number part.
-
Q: Is there a quicker method for converting simple fractions like 1/8 to decimals?
- A: Memorizing common fraction-to-decimal conversions can speed up calculations. For instance, knowing that 1/8 = 0.125 can save time.
-
Q: What about converting decimals back to fractions?
- A: The reverse process involves expressing the decimal as a fraction with a power of 10 as the denominator and then simplifying the fraction. For example, 0.125 can be written as 125/1000, which simplifies to 1/8.
Conclusion
Converting 5 1/8 to its decimal equivalent, 5.125, is a straightforward process achievable through several methods. Understanding the underlying principles of fractions and decimals is crucial not only for mastering this specific conversion but also for tackling more complex mathematical problems. This knowledge is applicable across numerous fields, highlighting the practical importance of mastering fraction-to-decimal conversions. Whether you use long division, convert to an improper fraction first, or use the more direct approach of converting the fraction and adding the whole number, the result remains the same – 5.125. Remember to practice regularly to build your confidence and proficiency in this fundamental mathematical skill.
Latest Posts
Latest Posts
-
What Is Spain People Called
Sep 09, 2025
-
How Far Is 55 Miles
Sep 09, 2025
-
Is 3 4 Bigger Than 2 3
Sep 09, 2025
-
1 Trillion Seconds In Years
Sep 09, 2025
-
Flowchart Of Classification Of Matter
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about 5 1/8 In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.