Is 3/4 Bigger Than 2/3
straightsci
Sep 09, 2025 · 6 min read
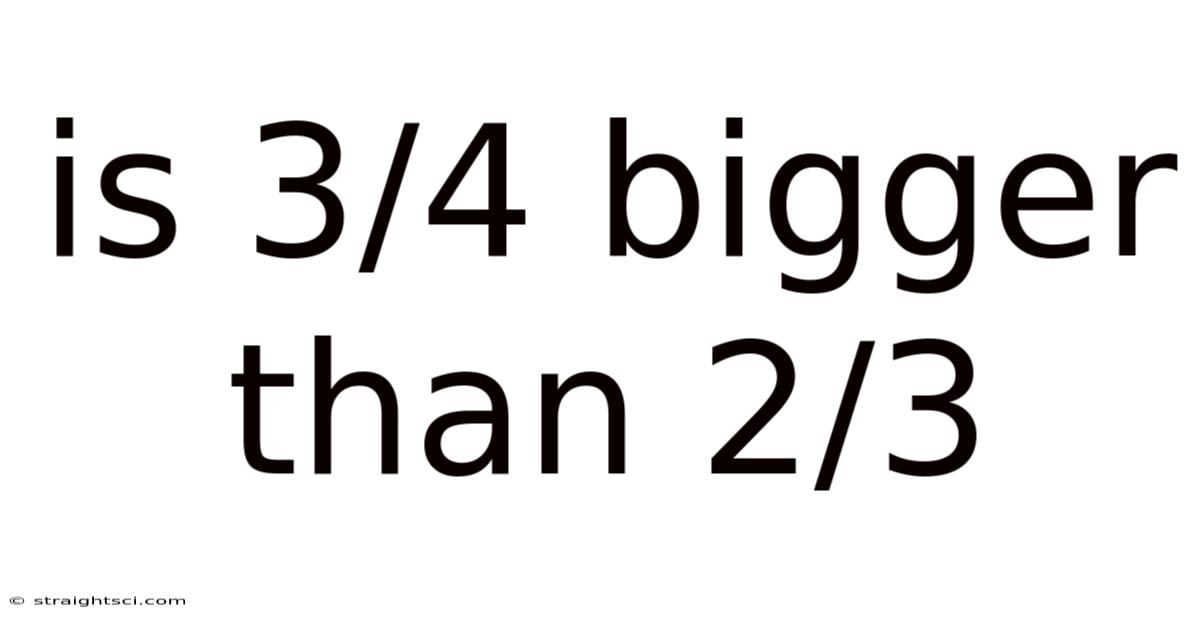
Table of Contents
Is 3/4 Bigger Than 2/3? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for everyday life and advanced studies. This article will comprehensively address the question: is 3/4 bigger than 2/3? We'll explore several methods for comparing fractions, providing a clear and intuitive understanding, suitable for learners of all levels. We'll delve into the underlying mathematical principles and dispel any confusion surrounding fraction comparison.
Introduction: Understanding Fractions
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), separated by a line. The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/4, the numerator (3) tells us we have three parts, and the denominator (4) tells us the whole is divided into four equal parts.
Method 1: Finding a Common Denominator
The most straightforward method to compare fractions is to find a common denominator. This means finding a number that is a multiple of both denominators. Once we have a common denominator, we can directly compare the numerators.
Let's compare 3/4 and 2/3. The denominators are 4 and 3. The least common multiple (LCM) of 4 and 3 is 12. We'll convert both fractions to have a denominator of 12:
- 3/4: To get a denominator of 12, we multiply both the numerator and denominator by 3: (3 x 3) / (4 x 3) = 9/12
- 2/3: To get a denominator of 12, we multiply both the numerator and denominator by 4: (2 x 4) / (3 x 4) = 8/12
Now we can easily compare: 9/12 is greater than 8/12. Therefore, 3/4 is bigger than 2/3.
Method 2: Converting to Decimals
Another effective way to compare fractions is by converting them to decimals. To convert a fraction to a decimal, we simply divide the numerator by the denominator.
- 3/4: 3 ÷ 4 = 0.75
- 2/3: 2 ÷ 3 = 0.666... (a repeating decimal)
Comparing the decimal values, 0.75 is clearly greater than 0.666... Again, we confirm that 3/4 is bigger than 2/3. This method is particularly useful when dealing with fractions that are difficult to convert to a common denominator.
Method 3: Visual Representation
A visual approach can be highly beneficial, especially for beginners. Imagine two identical circles.
- Divide the first circle into four equal parts and shade three of them (representing 3/4).
- Divide the second circle into three equal parts and shade two of them (representing 2/3).
By visually comparing the shaded areas, it's apparent that the shaded area in the first circle (3/4) is larger than the shaded area in the second circle (2/3). This provides a concrete, intuitive understanding of the comparison.
Method 4: Cross-Multiplication
Cross-multiplication offers a quick and efficient method for comparing fractions. We multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa. Then we compare the resulting products.
- 3/4 and 2/3:
- Multiply 3 (numerator of the first fraction) by 3 (denominator of the second fraction): 3 x 3 = 9
- Multiply 4 (denominator of the first fraction) by 2 (numerator of the second fraction): 4 x 2 = 8
Since 9 > 8, 3/4 is bigger than 2/3.
Explaining the Difference: Why 3/4 is Larger
The difference between 3/4 and 2/3 might seem small, but understanding why 3/4 is larger is crucial for developing a strong grasp of fractions. Let's break it down:
Imagine a pizza. If you divide the pizza into four equal slices (denominator of 3/4) and take three of them, you have a larger portion than if you divide the same-sized pizza into three equal slices (denominator of 2/3) and take two. The larger the denominator, the smaller each individual slice becomes. However, the numerator compensates for this in the case of 3/4. You're taking three of the smaller slices, which cumulatively results in a larger portion compared to taking two of the larger slices in 2/3.
Further Exploration: Working with More Complex Fractions
The methods discussed above are applicable to more complex fractions as well. For example, let’s compare 7/12 and 5/8.
Using the common denominator method:
- The LCM of 12 and 8 is 24.
- 7/12 = (7 x 2) / (12 x 2) = 14/24
- 5/8 = (5 x 3) / (8 x 3) = 15/24
Therefore, 5/8 > 7/12.
Using the decimal method:
- 7/12 ≈ 0.583
- 5/8 = 0.625
Again, we see that 5/8 > 7/12.
Frequently Asked Questions (FAQs)
Q: Are there any shortcuts for comparing simple fractions?
A: Sometimes, you can visually estimate the size of the fraction based on their proximity to 1/2 or 1. For example, 3/4 is clearly closer to 1 than 2/3.
Q: What if the fractions have very large denominators?
A: The common denominator method might become cumbersome with very large denominators. In such cases, converting to decimals or using cross-multiplication is more efficient.
Q: Why is understanding fraction comparison important?
A: Understanding fraction comparison is essential for numerous applications in real life, from cooking and baking (measuring ingredients) to finance (calculating proportions and percentages) and construction (measuring lengths and areas). It's a fundamental building block for further mathematical studies.
Q: How can I practice comparing fractions?
A: Practice is key! You can find numerous online resources, worksheets, and interactive games that provide opportunities to practice comparing fractions using various methods.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental skill in mathematics. This article has explored several methods for effectively comparing fractions: finding a common denominator, converting to decimals, visual representation, and cross-multiplication. We have applied these methods to answer the initial question definitively: yes, 3/4 is bigger than 2/3. By understanding these methods and practicing regularly, you can confidently tackle more complex fraction comparison problems and build a strong foundation in mathematics. Remember to choose the method that works best for you and the specific fractions you are comparing. The key is to develop a deep understanding of the underlying principles and to practice consistently. Through understanding and practice, mastering fraction comparison will become second nature. This will empower you to tackle more advanced mathematical concepts with confidence.
Latest Posts
Latest Posts
-
200 Degrees Celsius To F
Sep 09, 2025
-
How Much Sugar In Tablespoon
Sep 09, 2025
-
Formula For Kg To Lbs
Sep 09, 2025
-
5 16 Inch In Mm
Sep 09, 2025
-
How To Find Accrued Interest
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Is 3/4 Bigger Than 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.