3 1/3 As A Decimal
straightsci
Aug 26, 2025 · 5 min read
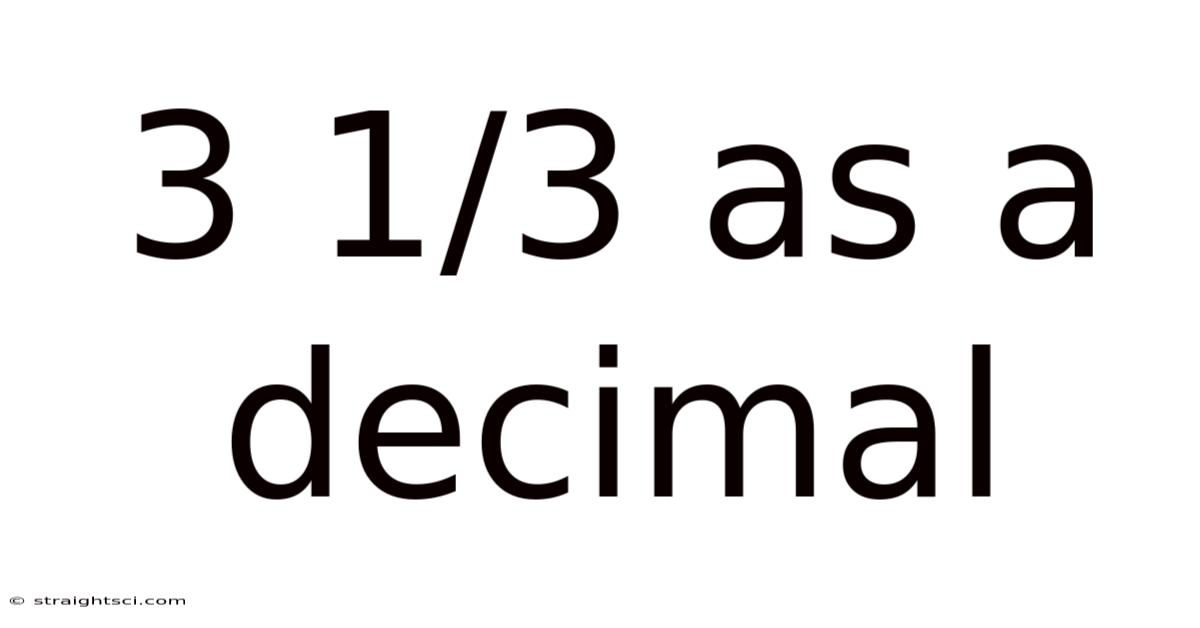
Table of Contents
Decoding 3 1/3 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This article provides a comprehensive explanation of how to convert the mixed number 3 1/3 into its decimal equivalent, exploring different methods and delving into the underlying mathematical principles. We'll cover various approaches, address common misconceptions, and even explore the practical applications of this conversion in everyday life. This guide aims to equip you with not just the answer, but a thorough understanding of the process.
Understanding Mixed Numbers and Decimals
Before diving into the conversion, let's clarify the terms involved. A mixed number combines a whole number and a fraction, like 3 1/3. A decimal, on the other hand, represents a number using a base-ten system, with a decimal point separating the whole number part from the fractional part (e.g., 3.333...). Converting a mixed number to a decimal means expressing the entire value using the decimal system.
Method 1: Converting the Fraction to a Decimal, then Adding the Whole Number
This is arguably the most straightforward method. We'll break down the process step-by-step:
-
Focus on the fraction: The mixed number 3 1/3 consists of a whole number (3) and a fraction (1/3). We'll initially focus on converting the fraction 1/3 to a decimal.
-
Division is key: To convert a fraction to a decimal, you perform division. Divide the numerator (the top number) by the denominator (the bottom number): 1 ÷ 3.
-
Performing the division: 1 ÷ 3 = 0.3333... Notice that this is a repeating decimal. The digit "3" repeats infinitely. We often represent repeating decimals using a bar over the repeating digit(s): 0.3̅.
-
Adding the whole number: Now, add the whole number part (3) to the decimal equivalent of the fraction (0.3̅): 3 + 0.3̅ = 3.3̅
Therefore, 3 1/3 as a decimal is 3.3̅ (or 3.333...).
Method 2: Converting the Mixed Number to an Improper Fraction First
This method involves an intermediate step of converting the mixed number into an improper fraction before performing the division.
-
Convert to an improper fraction: To convert 3 1/3 to an improper fraction, we multiply the whole number (3) by the denominator (3), add the numerator (1), and keep the same denominator: (3 * 3) + 1 = 10. The improper fraction is 10/3.
-
Perform the division: Now, divide the numerator (10) by the denominator (3): 10 ÷ 3 = 3.333... or 3.3̅
This method yields the same result: 3.3̅. Both methods are equally valid and demonstrate different approaches to the same problem.
Understanding Repeating Decimals
The result 3.3̅ highlights an important aspect of decimal representation: repeating decimals. A repeating decimal is a decimal number that has a digit or a sequence of digits that repeats infinitely. In this case, the digit "3" repeats infinitely. Understanding repeating decimals is crucial for working with fractions that have denominators that aren't factors of 10 (10, 100, 1000, etc.). Fractions with denominators that are factors of 10 will always result in terminating decimals (decimals that end).
Practical Applications of Decimal Conversions
Converting fractions to decimals is a crucial skill with numerous real-world applications:
-
Financial calculations: Dealing with money often involves fractions (e.g., calculating discounts, splitting bills, interest rates). Converting fractions to decimals simplifies these calculations.
-
Measurement and engineering: Many measurements involve fractions (e.g., inches, centimeters). Converting them to decimals is essential for precise calculations in engineering and construction.
-
Data analysis: In statistics and data analysis, representing data as decimals is often preferred for computational efficiency and ease of analysis.
-
Programming and computer science: Computers operate using binary numbers, but decimal representation is often used for input and output, requiring conversions between fractions and decimals.
Addressing Common Misconceptions
-
Rounding: While it's sometimes necessary to round repeating decimals for practical purposes, it's important to understand that 3.3̅ is not exactly equal to 3.33 or 3.333. It's an infinitely repeating decimal.
-
Approximations: When working with repeating decimals, it is crucial to maintain awareness that any truncated version is only an approximation of the true value. The more decimal places you use, the closer the approximation will be.
-
Calculators: Calculators may display a slightly truncated version of a repeating decimal due to their limited display capacity. Keep in mind that the true value is the repeating decimal.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to convert 3 1/3 to a decimal?
A: Yes, you can. Most calculators will give you 3.333... However, remember that the display might truncate the repeating decimal, and the precise answer is 3.3̅.
Q: Why is 1/3 a repeating decimal?
A: Because the denominator (3) is not a factor of 10 (or any power of 10). When the denominator cannot be simplified to a factor of 10, the resulting decimal will be repeating.
Q: How do I represent 3.3̅ in written form without using the bar notation?
A: You can write it as 3.333..., indicating that the "3" repeats indefinitely. However, the bar notation (3.3̅) is a more concise and accurate way to represent repeating decimals.
Q: Are there any other fractions that result in repeating decimals?
A: Yes, many. For example, 1/7, 1/9, 1/11, and 2/3 all result in repeating decimals. Generally, fractions with denominators that have prime factors other than 2 and 5 will result in repeating decimals.
Q: What is the significance of understanding repeating decimals?
A: Understanding repeating decimals is crucial for accurate mathematical calculations and prevents misinterpretations of values. It also provides insights into the relationship between fractions and decimal representations.
Conclusion
Converting 3 1/3 to a decimal, resulting in 3.3̅, is a straightforward process once you understand the underlying principles of fraction-to-decimal conversion. This article has demonstrated two distinct methods achieving the same result, clarified common misconceptions surrounding repeating decimals, and explored the practical applications of this conversion in various fields. Mastering this fundamental skill builds a strong foundation for more advanced mathematical concepts and problem-solving. Remember, while calculators can assist, a solid grasp of the underlying mathematical principles ensures accuracy and avoids relying solely on technology for understanding.
Latest Posts
Latest Posts
-
How Many Cups Is 400g
Aug 28, 2025
-
2 Equivalent Fractions For 2 3
Aug 28, 2025
-
Mean Deviation And Standard Deviation
Aug 28, 2025
-
How Many Employees At Target
Aug 28, 2025
-
How To Calculate Stockholders Equity
Aug 28, 2025
Related Post
Thank you for visiting our website which covers about 3 1/3 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.