2 Equivalent Fractions For 2/3
straightsci
Aug 28, 2025 · 6 min read
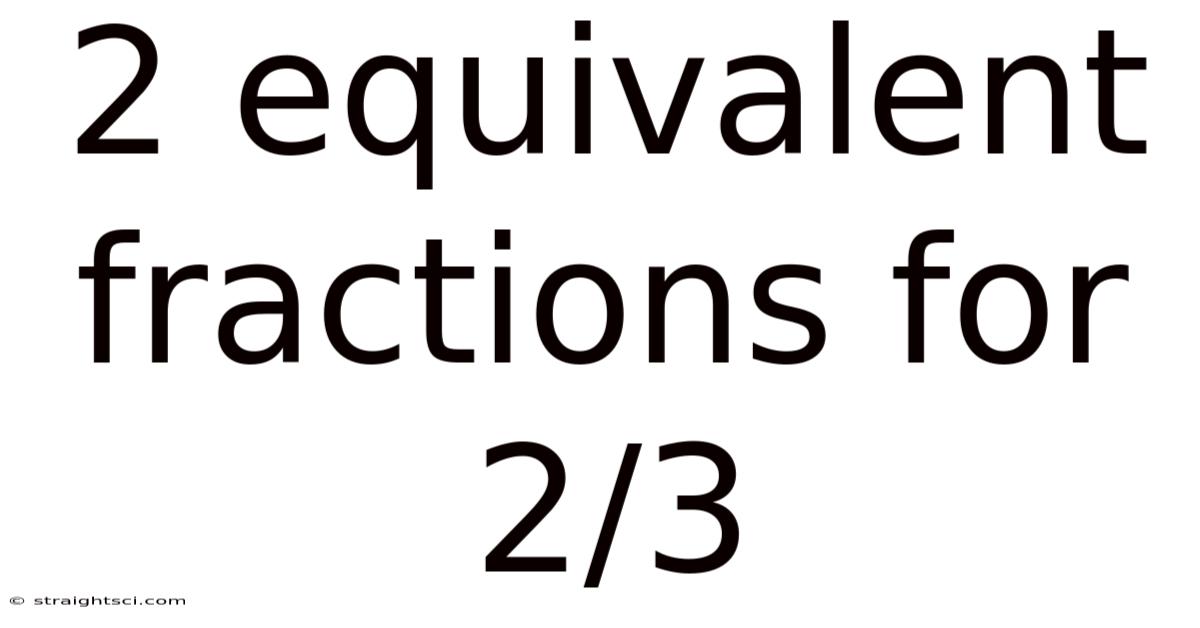
Table of Contents
Finding Two Equivalent Fractions for 2/3: A Deep Dive into Fraction Equivalence
Understanding equivalent fractions is a fundamental concept in mathematics, crucial for mastering various arithmetic operations and problem-solving. This article will explore the concept of equivalent fractions, focusing specifically on finding two equivalent fractions for 2/3. We'll delve into the underlying principles, explore multiple methods for finding these equivalents, and provide a solid foundation for understanding fraction equivalence more broadly. This will cover everything from the basic principles to more advanced considerations, making it a valuable resource for students and anyone looking to refresh their knowledge of fractions.
Understanding Equivalent Fractions
Equivalent fractions represent the same value even though they look different. Think of it like having a pizza: cutting the pizza into 6 slices and taking 4 slices gives you the same amount of pizza as cutting the pizza into 12 slices and taking 8 slices. Both represent 2/3 of the whole pizza. The key is that the ratio between the numerator (the top number) and the denominator (the bottom number) remains constant. This ratio represents the proportion of the whole.
In simpler terms: Equivalent fractions are different ways of expressing the same part of a whole.
Methods for Finding Equivalent Fractions of 2/3
There are several ways to find equivalent fractions for 2/3. Let's explore two primary methods:
Method 1: Multiplying the Numerator and Denominator by the Same Number
The fundamental principle of creating equivalent fractions is to multiply both the numerator and the denominator by the same non-zero number. This ensures the ratio remains unchanged, thus maintaining the same value.
Let's find two equivalent fractions for 2/3 using this method:
-
First Equivalent Fraction: We can multiply both the numerator (2) and the denominator (3) by 2:
(2 x 2) / (3 x 2) = 4/6
Therefore, 4/6 is an equivalent fraction to 2/3.
-
Second Equivalent Fraction: Now, let's multiply both the numerator and the denominator by 3:
(2 x 3) / (3 x 3) = 6/9
Therefore, 6/9 is another equivalent fraction to 2/3.
We could continue this process indefinitely, multiplying by 4, 5, 10, or any other non-zero number to generate an infinite number of equivalent fractions. This illustrates the concept that there are infinitely many equivalent fractions for any given fraction.
Method 2: Dividing the Numerator and Denominator by the Same Number (Simplification)
While the previous method creates equivalent fractions with larger numerators and denominators, we can also use division to find equivalent fractions with smaller numbers – this process is called simplification or reducing the fraction to its lowest terms. Although we are starting with 2/3 which is already in its simplest form, understanding this method is crucial for working with other fractions.
Let's consider a fraction equivalent to 2/3, for example, 12/18. To simplify this fraction and show its equivalence to 2/3, we find the greatest common divisor (GCD) of the numerator (12) and the denominator (18). The GCD of 12 and 18 is 6. Dividing both the numerator and the denominator by 6 gives:
(12 ÷ 6) / (18 ÷ 6) = 2/3
This demonstrates that 12/18 is indeed equivalent to 2/3. This method is essential for simplifying complex fractions and expressing them in their simplest form.
Visual Representation of Equivalent Fractions
Visual aids can greatly improve the understanding of equivalent fractions. Imagine representing 2/3 using a rectangular bar divided into three equal parts, with two of those parts shaded. Now imagine dividing each of the three parts into two smaller equal parts. You now have six smaller parts, and four of them are shaded (representing 4/6). The area represented remains the same, illustrating that 2/3 and 4/6 are equivalent. Similarly, dividing each of the original three parts into three smaller parts creates nine smaller parts, with six shaded (6/9), again showing the equivalence.
This visual representation clearly demonstrates that the ratio of shaded to unshaded areas remains consistent, regardless of the number of parts the whole is divided into.
The Importance of Equivalent Fractions
The concept of equivalent fractions is vital for several reasons:
-
Comparing Fractions: To compare fractions with different denominators, you need to find equivalent fractions with a common denominator. This allows for easy comparison of their relative sizes.
-
Adding and Subtracting Fractions: Adding and subtracting fractions requires a common denominator. Finding equivalent fractions is crucial for performing these operations accurately.
-
Simplifying Fractions: Simplifying fractions makes them easier to work with and understand. It presents the fraction in its most concise form.
-
Problem Solving: Many real-world problems involve fractions, and understanding equivalent fractions is essential for accurate solutions.
Frequently Asked Questions (FAQ)
Q1: Are there infinitely many equivalent fractions for 2/3?
A1: Yes, there are infinitely many equivalent fractions for 2/3. You can generate new equivalents by multiplying the numerator and denominator by any non-zero integer.
Q2: How do I know if two fractions are equivalent?
A2: Two fractions are equivalent if the ratio of their numerator to their denominator is the same. You can check this by simplifying both fractions to their lowest terms. If they simplify to the same fraction, they are equivalent. Alternatively, you can cross-multiply: if the products are equal, the fractions are equivalent. For example, for 2/3 and 4/6: (2 x 6) = (3 x 4) = 12.
Q3: Why is it important to simplify fractions?
A3: Simplifying fractions makes them easier to understand and work with. It presents the fraction in its most concise and manageable form. Furthermore, simplified fractions are often easier to compare and use in calculations.
Q4: Can I use decimals to represent equivalent fractions?
A4: Yes. The decimal representation of 2/3 is approximately 0.666... (a repeating decimal). Equivalent fractions will also have the same decimal representation (or a close approximation due to rounding in the case of repeating decimals). For example, 4/6 and 6/9 will both also result in approximately 0.666... when converted to decimals.
Conclusion
Finding equivalent fractions for 2/3, or any fraction, is a fundamental skill in mathematics. By understanding the underlying principles and mastering the methods outlined above, you can confidently generate equivalent fractions, simplify fractions, and apply these concepts to solve a wide range of mathematical problems. Remember, the key is to maintain the ratio between the numerator and the denominator. Practice is crucial to solidifying this understanding. Consistent practice with different fractions will build your fluency and confidence in working with fractions, paving the way for success in more advanced mathematical concepts. Through understanding and applying these techniques, you can navigate the world of fractions with ease and precision.
Latest Posts
Latest Posts
-
What Is A Grammatical Subject
Aug 28, 2025
-
Function Of Pons In Brain
Aug 28, 2025
-
Abiotic Characteristics Of Tropical Rainforest
Aug 28, 2025
-
Formula For Cube Surface Area
Aug 28, 2025
-
What Does Connotative Meaning Mean
Aug 28, 2025
Related Post
Thank you for visiting our website which covers about 2 Equivalent Fractions For 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.