2x - 5x - 10
straightsci
Sep 13, 2025 · 6 min read
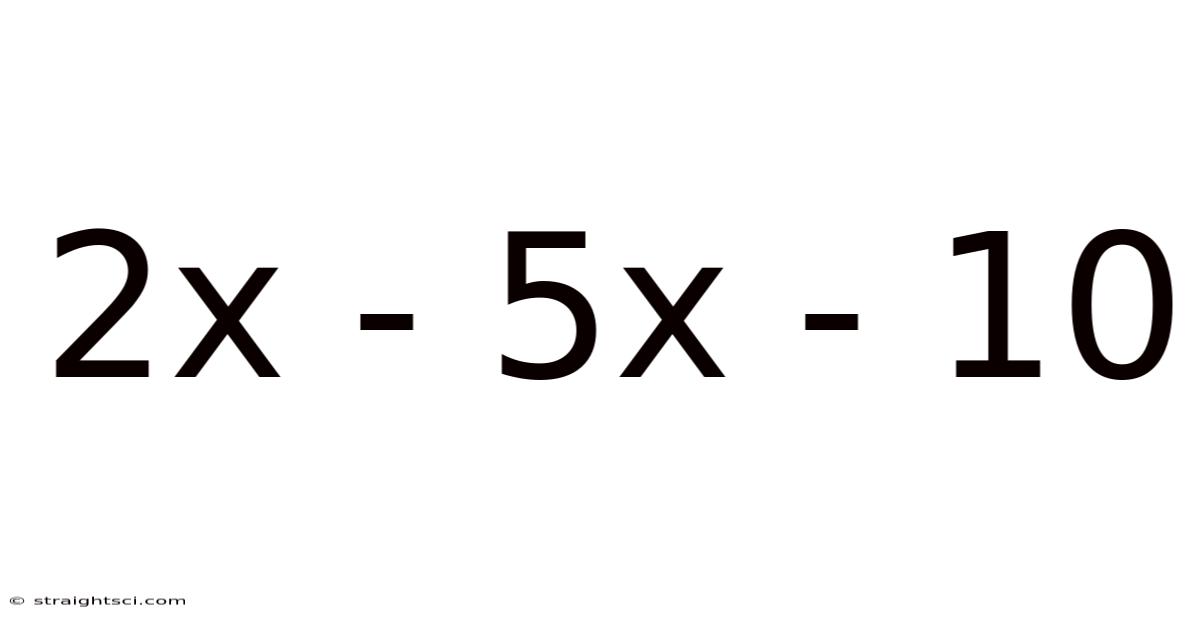
Table of Contents
Exploring the Quadratic Expression: 2x² - 5x - 10
This article delves into the quadratic expression 2x² - 5x - 10, exploring its various properties, how to solve it, and its applications in mathematics and beyond. We'll cover everything from finding its roots (or zeros) using different methods – factoring, the quadratic formula, and completing the square – to understanding its graphical representation and interpreting its meaning in real-world contexts. Whether you're a high school student tackling algebra or someone looking to refresh their mathematical knowledge, this comprehensive guide will equip you with the necessary tools to confidently work with this type of expression.
Understanding Quadratic Expressions
Before we dive into the specifics of 2x² - 5x - 10, let's establish a foundational understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, x) is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants, and a is not equal to zero (otherwise, it wouldn't be a quadratic). In our specific example, 2x² - 5x - 10, we have a = 2, b = -5, and c = -10.
Understanding the structure of a quadratic expression is crucial for manipulating and solving it. The constants a, b, and c determine the shape and position of the parabola, the curve representing the quadratic function when graphed. The value of a dictates whether the parabola opens upwards (a > 0) or downwards (a < 0). The vertex of the parabola, its highest or lowest point, is also directly related to these constants.
Finding the Roots of 2x² - 5x - 10
The roots, or zeros, of a quadratic expression are the values of x that make the expression equal to zero. Finding these roots is a fundamental aspect of working with quadratic expressions. There are several methods we can employ to find the roots of 2x² - 5x - 10:
1. Factoring
Factoring involves expressing the quadratic expression as a product of two linear expressions. Unfortunately, 2x² - 5x - 10 doesn't factor neatly using integers. We can try various combinations, but we won't find two numbers that multiply to -20 (2 * -10) and add up to -5. This indicates that the roots are not rational numbers.
2. The Quadratic Formula
The quadratic formula provides a direct method for finding the roots of any quadratic expression of the form ax² + bx + c. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our expression (a = 2, b = -5, c = -10), we get:
x = [5 ± √((-5)² - 4 * 2 * -10)] / (2 * 2)
x = [5 ± √(25 + 80)] / 4
x = [5 ± √105] / 4
Therefore, the roots of 2x² - 5x - 10 are:
x₁ = (5 + √105) / 4 ≈ 3.127
x₂ = (5 - √105) / 4 ≈ -1.627
These are irrational roots, meaning they cannot be expressed as simple fractions.
3. Completing the Square
Completing the square is another algebraic method for solving quadratic equations. It involves manipulating the expression to create a perfect square trinomial, which can then be easily factored. While possible, completing the square for 2x² - 5x - 10 is more complex than using the quadratic formula in this instance. It involves dividing by the coefficient of x², manipulating the constant term, and then taking the square root. The result, naturally, will be the same irrational roots we found using the quadratic formula.
Graphical Representation
The quadratic expression 2x² - 5x - 10 represents a parabola when graphed on a coordinate plane. Because the coefficient of x² (a = 2) is positive, the parabola opens upwards. The roots we calculated, (5 + √105) / 4 and (5 - √105) / 4, represent the x-intercepts – the points where the parabola intersects the x-axis.
The vertex of the parabola, the point where the parabola reaches its minimum value, can be found using the formula:
x-coordinate of vertex = -b / 2a = -(-5) / (2 * 2) = 5/4 = 1.25
To find the y-coordinate, substitute x = 1.25 back into the original expression:
y = 2(1.25)² - 5(1.25) - 10 = 3.125 - 6.25 - 10 = -13.125
Therefore, the vertex of the parabola is (1.25, -13.125). This point represents the minimum value of the quadratic function.
Applications of Quadratic Expressions
Quadratic expressions are not merely abstract mathematical concepts; they have numerous applications in various fields:
-
Physics: Projectile motion, where an object is thrown or launched into the air, is often modeled using quadratic equations. The height of the object over time follows a parabolic path.
-
Engineering: Quadratic equations are used in structural design to calculate stresses, strains, and deflections in beams and other structural elements.
-
Economics: Quadratic functions can model cost, revenue, and profit functions in business and economics. Finding the maximum profit or minimum cost often involves solving a quadratic equation.
-
Computer Graphics: Parabolas are used to create curved lines and shapes in computer graphics and animation.
-
Optimization Problems: Many optimization problems involve finding the maximum or minimum value of a function, and quadratic functions are frequently encountered in such problems.
Frequently Asked Questions (FAQ)
Q: What is the discriminant of the quadratic expression 2x² - 5x - 10?
A: The discriminant is the part of the quadratic formula under the square root: b² - 4ac. In this case, it's (-5)² - 4(2)(-10) = 105. A positive discriminant indicates that the quadratic equation has two distinct real roots, as we found.
Q: How can I determine the axis of symmetry of the parabola?
A: The axis of symmetry is a vertical line that passes through the vertex of the parabola. Its equation is given by x = -b / 2a. For our expression, the axis of symmetry is x = 5/4 or x = 1.25.
Q: Can I solve this quadratic equation using a graphing calculator?
A: Yes, you can graph the function y = 2x² - 5x - 10 on a graphing calculator and find the x-intercepts (roots) using the calculator's features. This provides a visual representation of the solution and can be a helpful way to verify the results obtained algebraically.
Q: What if the discriminant was negative?
A: If the discriminant (b² - 4ac) were negative, it would indicate that the quadratic equation has no real roots. The parabola would not intersect the x-axis. The roots would be complex numbers involving the imaginary unit i.
Q: Are there other methods to solve quadratic equations besides those mentioned?
A: Yes, numerical methods such as the Newton-Raphson method can be used to approximate the roots of a quadratic equation, particularly when analytical methods are difficult or impractical.
Conclusion
The quadratic expression 2x² - 5x - 10, while seemingly simple, offers a rich opportunity to explore fundamental concepts in algebra and their applications. Understanding how to find its roots using different methods, visualizing its graphical representation, and appreciating its relevance in various fields is crucial for developing a strong mathematical foundation. This article provided a detailed overview, equipping you with the tools and knowledge to confidently tackle similar quadratic expressions and further explore the fascinating world of mathematics. Remember, practice is key to mastering these concepts, so keep experimenting and solving different quadratic expressions to solidify your understanding.
Latest Posts
Latest Posts
-
M Y2 Y1 X2 X1
Sep 13, 2025
-
Conduction Vs Convection Vs Radiation
Sep 13, 2025
-
Four Types Of Reactions Chemistry
Sep 13, 2025
-
Anatomy Pelvic Floor Muscles Female
Sep 13, 2025
-
5 5 Ft In Inches
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 2x - 5x - 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.