M Y2 Y1 X2 X1
straightsci
Sep 13, 2025 · 6 min read
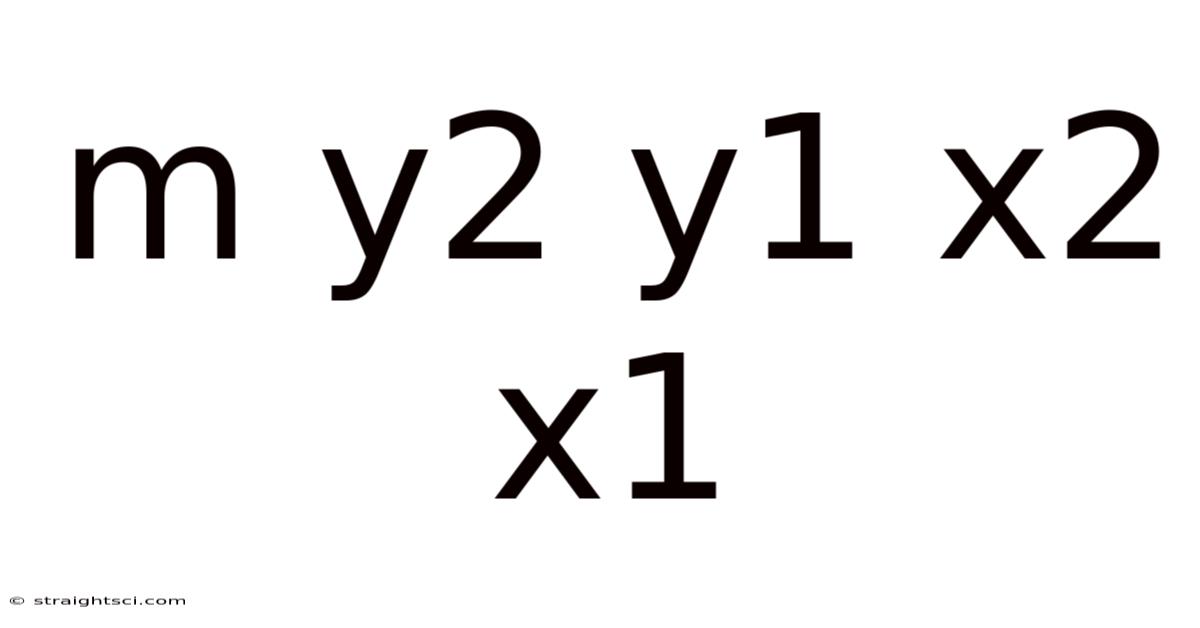
Table of Contents
Understanding the Slope: Delving Deep into (y2 - y1) / (x2 - x1)
The formula (y2 - y1) / (x2 - x1) is a cornerstone of algebra and geometry, representing the slope of a line connecting two points on a coordinate plane. Understanding this seemingly simple equation unlocks a deeper understanding of linear relationships, functions, and even more complex mathematical concepts. This article will provide a comprehensive exploration of this formula, covering its derivation, practical applications, interpretations, and frequently asked questions.
Introduction: What Does (y2 - y1) / (x2 - x1) Actually Mean?
At its core, (y2 - y1) / (x2 - x1) calculates the rate of change between two points on a graph. Imagine you're plotting points on a map. Each point has a specific x-coordinate (horizontal position) and a y-coordinate (vertical position). The formula takes two points, (x1, y1) and (x2, y2), and compares their vertical and horizontal differences. The numerator (y2 - y1) represents the change in the vertical direction (the "rise"), while the denominator (x2 - x1) represents the change in the horizontal direction (the "run"). Therefore, the slope is essentially the ratio of "rise over run." A positive slope indicates an upward trend, a negative slope indicates a downward trend, a slope of zero represents a horizontal line, and an undefined slope represents a vertical line.
Deriving the Slope Formula: A Visual Approach
Let's visualize how this formula is derived. Consider two points, A(x1, y1) and B(x2, y2), on a Cartesian coordinate system. We can create a right-angled triangle using these points, with the line segment AB as the hypotenuse. The vertical leg of this triangle has length (y2 - y1), and the horizontal leg has length (x2 - x1). The slope, often represented by the letter m, is defined as the tangent of the angle θ formed by the line AB and the positive x-axis. From trigonometry, we know that tan(θ) = opposite/adjacent. In our triangle, the opposite side is (y2 - y1) and the adjacent side is (x2 - x1). Therefore, the slope m = (y2 - y1) / (x2 - x1).
Practical Applications: Where Do We Use This Formula?
The slope formula isn't just a theoretical concept; it finds extensive use in various fields:
-
Physics: Calculating the velocity or acceleration of an object. If you plot the distance traveled against time, the slope of the resulting line represents the velocity. Similarly, the slope of a velocity-time graph gives the acceleration.
-
Engineering: Designing slopes for roads, ramps, and other structures. Engineers use the slope formula to ensure safety and functionality.
-
Economics: Analyzing trends in economic data. For example, plotting the price of a commodity over time allows for the calculation of the average rate of price change using the slope.
-
Finance: Determining the rate of return on investments. The slope of a graph showing the value of an investment over time represents the average rate of return.
-
Computer Graphics: Creating lines and other geometric shapes on a screen. The slope is crucial for determining the direction and angle of lines.
-
Machine Learning: Linear regression models heavily rely on calculating the slope to best fit a line through a set of data points. The slope represents the relationship between the independent and dependent variables.
Interpreting the Slope: Beyond Just a Number
The numerical value of the slope carries significant meaning:
-
Positive Slope (m > 0): Indicates a positive correlation between x and y. As x increases, y increases. The steeper the line (larger the slope), the stronger the positive relationship.
-
Negative Slope (m < 0): Indicates a negative correlation between x and y. As x increases, y decreases. The steeper the downward slope (larger the absolute value), the stronger the negative relationship.
-
Zero Slope (m = 0): Represents a horizontal line. There is no change in y as x changes. This indicates no correlation between x and y.
-
Undefined Slope (m is undefined): Represents a vertical line. The denominator (x2 - x1) is zero, meaning the change in x is zero. This signifies that x remains constant regardless of the change in y.
Different Forms of the Equation of a Line
The slope formula is fundamental to deriving various forms of the equation of a line:
-
Slope-intercept form (y = mx + b): This form is particularly useful because it directly shows the slope (m) and the y-intercept (b – the point where the line crosses the y-axis). Given the slope and one point, you can easily find the equation of the line.
-
Point-slope form (y - y1 = m(x - x1)): This form is helpful when you know the slope (m) and one point (x1, y1) on the line.
-
Standard form (Ax + By = C): This form is often used for simplicity and ease of manipulation in certain algebraic operations.
Understanding the relationship between these forms is crucial for solving various problems involving lines. You can convert between these forms using algebraic manipulation.
Handling Special Cases: Vertical and Horizontal Lines
As mentioned earlier, the slope formula requires careful consideration for vertical and horizontal lines:
-
Horizontal lines: For a horizontal line, y remains constant, meaning y2 = y1. This results in a slope of m = (y2 - y1) / (x2 - x1) = 0 / (x2 - x1) = 0.
-
Vertical lines: For a vertical line, x remains constant, meaning x2 = x1. This results in a slope of m = (y2 - y1) / (x2 - x1) = (y2 - y1) / 0, which is undefined. Division by zero is not allowed in mathematics.
Advanced Concepts: Parallel and Perpendicular Lines
The slope plays a critical role in determining the relationship between two lines:
-
Parallel lines: Parallel lines have the same slope. If two lines are parallel, their slopes are equal (m1 = m2).
-
Perpendicular lines: Perpendicular lines have negative reciprocal slopes. If two lines are perpendicular, the product of their slopes is -1 (m1 * m2 = -1). This means that the slope of one line is the negative inverse of the slope of the other line.
Frequently Asked Questions (FAQ)
-
Q: What if my points are not neatly aligned on the grid?
*A: The slope formula works perfectly well for points with non-integer coordinates. Simply substitute the precise x and y values into the formula and calculate the slope.
-
Q: How can I find the equation of a line given two points?
*A: 1. First, calculate the slope using the formula (y2 - y1) / (x2 - x1). 2. Then, use either the point-slope form or slope-intercept form to write the equation of the line.
-
Q: Can I use this formula for curves?
*A: No, this formula is specifically for straight lines. For curves, you need to use calculus to find the slope (which is the derivative at a specific point).
-
Q: What does a slope of 1 mean?
*A: A slope of 1 means that for every 1 unit increase in x, there is a 1 unit increase in y. The line makes a 45-degree angle with the positive x-axis.
-
Q: Why is the slope important in real-world applications?
*A: The slope quantifies the rate of change. Understanding this rate of change is crucial for making predictions, understanding trends, and designing systems in various fields.
Conclusion: Mastering the Slope
The seemingly simple formula (y2 - y1) / (x2 - x1) is a powerful tool with far-reaching applications. By understanding its derivation, interpretations, and various forms, you gain a robust foundation in linear algebra and its applications across numerous disciplines. This formula is not just a mathematical concept; it's a key to unlocking insights in data analysis, scientific modeling, and engineering design. Mastering the slope opens doors to a deeper comprehension of the world around us, revealing the hidden relationships and patterns within data.
Latest Posts
Latest Posts
-
Elevation Salt Lake City Utah
Sep 13, 2025
-
How Many Innings In Baseball
Sep 13, 2025
-
Is Hydro Latin Or Greek
Sep 13, 2025
-
Convert 12 Oz To Ml
Sep 13, 2025
-
How To Factor The Expression
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about M Y2 Y1 X2 X1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.