2 X 3 X 5
straightsci
Sep 21, 2025 · 7 min read
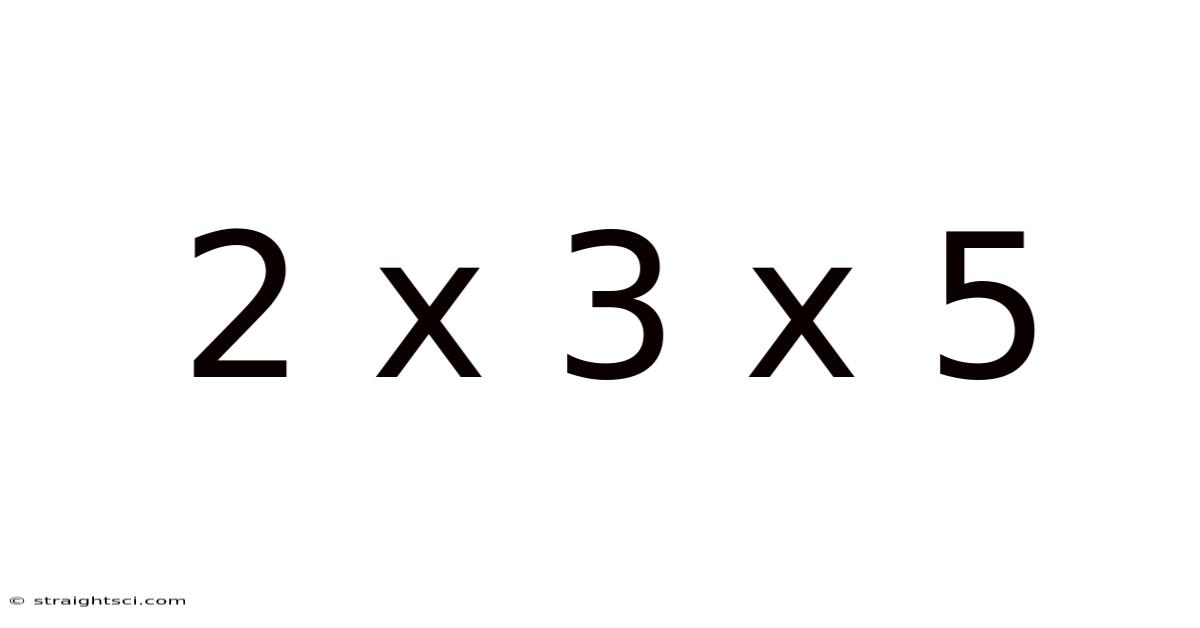
Table of Contents
Unveiling the Mysteries of 2 x 3 x 5: A Deep Dive into Prime Factorization and Beyond
This seemingly simple equation, 2 x 3 x 5, opens a door to a vast world of mathematical concepts. It's more than just a multiplication problem; it's a prime factorization, a building block of number theory, and a gateway to understanding complex mathematical structures. This article will explore the equation in detail, delving into its implications in various mathematical fields and highlighting its significance in everyday life. We'll unpack the concepts of prime numbers, factorization, and the importance of this specific combination – 30 – in various contexts.
Understanding Prime Numbers: The Building Blocks of Arithmetic
Before diving into the intricacies of 2 x 3 x 5, let's establish a firm understanding of prime numbers. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. This means it cannot be factored into smaller whole numbers other than 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. These numbers are the fundamental building blocks of all other whole numbers, much like atoms are the building blocks of matter. They are indivisible in the sense of whole number division.
The number 2 holds a unique position as the only even prime number. All other even numbers are divisible by 2, hence not prime. The significance of prime numbers lies in their irreducibility; they cannot be broken down further into simpler whole number factors.
Prime Factorization: Deconstructing Numbers into their Prime Components
Prime factorization is the process of expressing a whole number as a product of its prime factors. Every whole number greater than 1 can be uniquely expressed as a product of prime numbers. This unique representation is known as the Fundamental Theorem of Arithmetic. This theorem is a cornerstone of number theory, providing a fundamental way to understand the structure of whole numbers.
Let's consider our equation, 2 x 3 x 5 = 30. This equation demonstrates the prime factorization of 30. The numbers 2, 3, and 5 are all prime numbers, and they are the only prime numbers that, when multiplied together, equal 30. This factorization is unique; no other combination of prime numbers will result in 30.
The Significance of 2 x 3 x 5 = 30
The number 30 itself holds a certain mathematical charm. It's a highly composite number, meaning it has a relatively large number of divisors. Its divisors are 1, 2, 3, 5, 6, 10, 15, and 30. This abundance of divisors makes it relevant in various mathematical and practical applications.
-
Divisibility: The fact that 30 is divisible by 2, 3, and 5 makes it useful in divisibility rules. For example, a number is divisible by 30 if it's divisible by 2, 3, and 5 simultaneously. This property simplifies divisibility checks.
-
Combinatorics: The number 30 frequently appears in combinatorial problems. For example, it's the number of ways to arrange three distinct objects in a row (3! = 3 x 2 x 1 = 6) multiplied by five distinct objects (5 choices for the first position, 4 for the second, 3 for the third, 2 for the fourth, 1 for the fifth. While this exact application doesn't directly correlate to 2 x 3 x 5, it illustrates the importance of understanding how prime numbers combine to create composite numbers.
-
Calendar Systems: The number 30 is used in some calendar systems, representing the number of days in some months. Although many modern calendars use 31, the number 30 carries historical weight.
-
Geometry: The number 30 appears in various geometric contexts, such as angles in triangles (30-60-90 triangle). The relation between these angles is again tied to the underlying factorisation and mathematical ratios that can be expressed through prime numbers.
Beyond the Basics: Exploring Advanced Concepts
The seemingly simple equation 2 x 3 x 5 = 30 opens doors to more advanced mathematical concepts:
-
Modular Arithmetic: This branch of number theory deals with remainders after division. The prime factorization of 30 is crucial in understanding modular arithmetic operations, especially concerning modulo 30 calculations.
-
Number Theory: The prime factorization of numbers is fundamental to many areas within number theory, including the study of prime number distribution, Diophantine equations, and cryptography. Understanding the prime factorization of a number is a fundamental step in analyzing many complex mathematical problems.
-
Cryptography: Prime numbers play a crucial role in modern cryptography, particularly in RSA encryption. The security of RSA relies on the difficulty of factoring large numbers into their prime components. The basic principles are illustrated in the seemingly simple factorization we are studying.
-
Abstract Algebra: The concepts of prime factorization extend to more abstract mathematical structures, such as rings and fields, where the notion of prime elements generalizes the concept of prime numbers. This is where the importance of understanding these fundamental building blocks reaches an even deeper level.
Practical Applications: From Everyday Life to Advanced Technology
While prime factorization might seem like an abstract mathematical concept, it has far-reaching practical applications:
-
Computer Science: Efficient algorithms for prime factorization are crucial in computer science, particularly in cryptography and data security. The ability to quickly factor large numbers would break many widely used encryption methods.
-
Coding Theory: Prime numbers and their properties are fundamental in coding theory, which is used to detect and correct errors in data transmission and storage.
-
Data Compression: Prime factorization can be applied to optimize data compression algorithms. Understanding the building blocks of numbers allows for more efficient compression.
Frequently Asked Questions (FAQ)
Q: Why are prime numbers important?
A: Prime numbers are the fundamental building blocks of all whole numbers. Every whole number greater than 1 can be uniquely expressed as a product of prime numbers (Fundamental Theorem of Arithmetic). This unique factorization is crucial in various mathematical fields and applications.
Q: How do I find the prime factorization of a number?
A: There are several methods to find the prime factorization of a number. One common method involves repeatedly dividing the number by the smallest prime number until you are left with 1. Another method uses factor trees. Both methods ensure that you are only left with prime numbers at the end of the decomposition.
Q: What is the significance of the number 30?
A: The number 30, being 2 x 3 x 5, is a highly composite number with many divisors. This makes it relevant in various contexts, from divisibility rules to calendar systems and even some geometric applications. Its abundance of factors makes it a useful number in many mathematical and practical scenarios.
Q: Are there infinitely many prime numbers?
A: Yes, this is a fundamental theorem in number theory. Euclid's proof demonstrates that there are infinitely many prime numbers. This infinite supply of primes is essential to the structure of mathematics.
Conclusion: The Enduring Importance of 2 x 3 x 5
The seemingly simple equation 2 x 3 x 5 = 30 serves as a microcosm of the vast and intricate world of mathematics. It encapsulates the fundamental concepts of prime numbers, prime factorization, and the power of these building blocks in various mathematical disciplines and practical applications. From cryptography and computer science to the seemingly simple act of checking for divisibility, the underlying principles demonstrated in this equation are essential for understanding the structure of numbers and their significance in the world around us. The journey from a simple multiplication problem to the exploration of abstract algebra and cryptography underscores the enduring importance of seemingly simple mathematical concepts. The exploration of 2 x 3 x 5 not only answers the question of the equation's value, but also sparks curiosity and lays the foundation for deeper understanding in the rich world of numbers and mathematics.
Latest Posts
Latest Posts
-
Command To Refresh Group Policy
Sep 21, 2025
-
Bitter Taste Acid Or Base
Sep 21, 2025
-
Convert Mph To Ft S
Sep 21, 2025
-
Proximal Surface Of A Tooth
Sep 21, 2025
-
6 Kilos How Many Pounds
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 2 X 3 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.