2 3 X 6 6
straightsci
Sep 25, 2025 · 5 min read
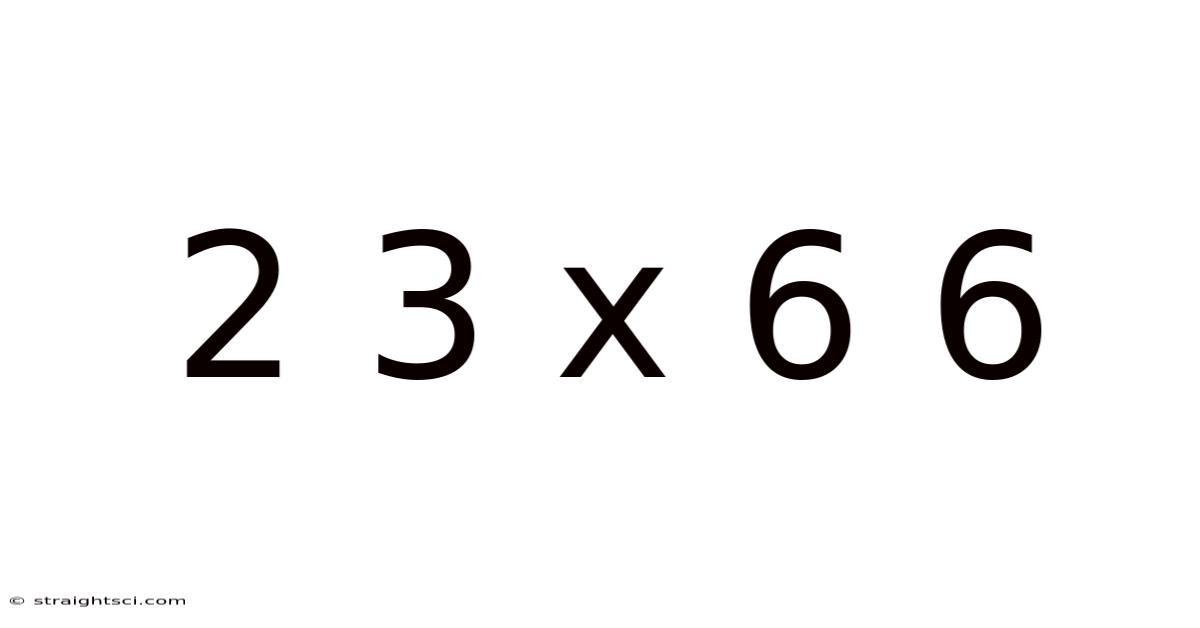
Table of Contents
Unveiling the Mysteries of 23 x 66: A Deep Dive into Multiplication and Beyond
This article explores the seemingly simple multiplication problem, 23 x 66, and uses it as a springboard to delve into various mathematical concepts, exploring different calculation methods, the underlying principles, and the broader applications of multiplication in everyday life and advanced fields. We'll move beyond the basic answer and uncover the richness and beauty hidden within this seemingly straightforward equation. This exploration will be accessible to a wide range of readers, from elementary school students grasping multiplication fundamentals to those seeking a refresher on mathematical techniques.
I. Introduction: More Than Just a Number
The multiplication problem 23 x 66 might seem insignificant at first glance. It's a calculation easily performed by a calculator or even mental math for those proficient in arithmetic. However, this seemingly simple equation provides an excellent opportunity to explore fundamental mathematical concepts and their practical applications. We'll investigate various methods for solving this problem, emphasizing the understanding behind the calculations rather than solely focusing on the final answer. This approach helps build a stronger mathematical foundation, fostering critical thinking and problem-solving skills. We will cover different calculation approaches, including standard multiplication, distributive property, and even mental math techniques. Beyond the calculation itself, we'll also explore the broader mathematical context, touching upon number theory, algebra, and the real-world applications of multiplication.
II. Solving 23 x 66: Different Approaches
Let's start with the most common method: standard long multiplication.
A. Standard Long Multiplication:
This method, taught in elementary schools, involves breaking down the multiplication into smaller, manageable steps:
23
x 66
-----
138 (23 x 6)
1380 (23 x 60)
-----
1518
This method systematically multiplies each digit of 23 by each digit of 66 and then adds the results. It's reliable and easy to understand, making it a fundamental building block for more advanced mathematical operations.
B. Distributive Property:
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can apply this property to solve 23 x 66 as follows:
23 x 66 = 23 x (60 + 6) = (23 x 60) + (23 x 6) = 1380 + 138 = 1518
This method highlights the underlying mathematical principle and can be particularly useful for mental calculations. Breaking down the larger numbers into smaller, more manageable parts makes the calculation easier to perform mentally.
C. Mental Math Techniques:
With practice, 23 x 66 can be solved mentally using various techniques. One approach involves rounding and adjustment:
- Round 23 to 20 and 66 to 70. 20 x 70 = 1400.
- Adjust for the rounding: 3 x 66 = 198 and 6 x 20 =120. The total adjustment is approximately 318.
- Add the adjustment to the rounded product: 1400 + 318 = 1718. This is a approximation, the actual number is 1518. This method illustrates that estimation and approximation are valuable mathematical skills.
D. Using a Calculator:
While not a method emphasizing understanding, calculators provide a quick and reliable way to solve this problem. However, over-reliance on calculators can hinder the development of crucial mathematical reasoning skills.
III. The Underlying Principles: A Deeper Dive
The solution to 23 x 66 relies on several fundamental mathematical principles:
- Place Value: The concept of place value, where the position of a digit determines its value (ones, tens, hundreds, etc.), is crucial in understanding long multiplication.
- Multiplication as Repeated Addition: Multiplication can be viewed as repeated addition. 23 x 66 means adding 23 sixty-six times.
- Associative and Commutative Properties: The associative property (a x (b x c) = (a x b) x c) and commutative property (a x b = b x a) apply to multiplication, allowing us to rearrange and group numbers for easier calculations.
Understanding these principles is essential for mastering multiplication and for tackling more complex mathematical problems.
IV. Applications of Multiplication: Beyond the Classroom
Multiplication isn't confined to textbooks and classrooms. It plays a vital role in numerous aspects of daily life and various professional fields.
A. Everyday Applications:
- Shopping: Calculating the total cost of multiple items.
- Cooking: Scaling recipes up or down.
- Travel: Determining distances based on speed and time.
- Finance: Calculating interest, taxes, or discounts.
B. Professional Applications:
- Engineering: Calculating dimensions, forces, and materials.
- Computer Science: Performing complex calculations and algorithms.
- Finance: Modeling financial markets and forecasting trends.
- Physics: Solving equations and modeling physical phenomena.
The ability to perform multiplication accurately and efficiently is a valuable skill in all these contexts.
V. Exploring Related Mathematical Concepts
The problem 23 x 66 provides a launchpad to explore more advanced mathematical concepts:
- Prime Factorization: Breaking down 23 and 66 into their prime factors (23 is a prime number, while 66 = 2 x 3 x 11) can provide insights into the structure of the numbers.
- Number Theory: Concepts like divisibility rules and greatest common divisors (GCD) can be explored using these numbers. 23 and 66 share no common factors other than 1, indicating that their GCD is 1.
- Algebra: The equation 23x = 1518 can be solved using algebraic techniques, highlighting the connection between arithmetic and algebra.
VI. Frequently Asked Questions (FAQs)
Q: What is the easiest way to multiply 23 x 66?
A: The easiest method depends on individual preference and skill level. For many, the standard long multiplication method is straightforward. For others, the distributive property or mental math techniques might be more efficient.
Q: Are there any tricks for mental multiplication?
A: Yes, many mental math tricks exist, including rounding and adjusting, using the distributive property, and recognizing patterns. Practice is key to mastering these techniques.
Q: Why is it important to understand the underlying principles of multiplication?
A: Understanding the underlying principles (place value, distributive property, etc.) builds a strong mathematical foundation, allowing for more efficient problem-solving and the ability to tackle more complex mathematical concepts in the future.
VII. Conclusion: The Value of Understanding
The seemingly simple multiplication problem 23 x 66 offers a rich opportunity for exploring fundamental mathematical concepts, different calculation methods, and the real-world applications of multiplication. Moving beyond the simple answer of 1518, we've uncovered the power of understanding underlying principles and the importance of developing strong mathematical reasoning skills. These skills are invaluable, extending far beyond the confines of the classroom and enriching our understanding of the world around us. The journey from a simple calculation to a broader understanding of mathematical principles underscores the beauty and practical value of mathematics in our lives. Mastering these fundamentals paves the way for exploring more complex mathematical ideas and confidently tackling challenges in various fields.
Latest Posts
Latest Posts
-
What Is Character Traits Mean
Sep 25, 2025
-
Hottest Part Of A Flame
Sep 25, 2025
-
Lcm Of 6 And 10
Sep 25, 2025
-
1 4 Ounce Yeast In Tsp
Sep 25, 2025
-
When Did America Enter Ww2
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 2 3 X 6 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.