Lcm Of 6 And 10
straightsci
Sep 25, 2025 · 6 min read
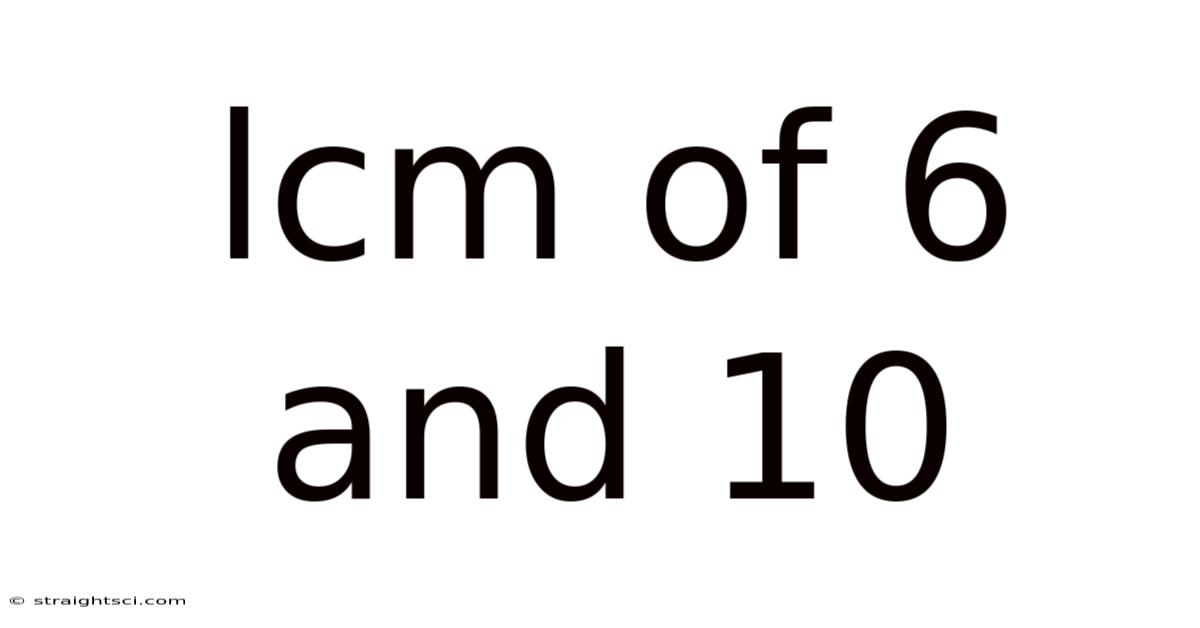
Table of Contents
Understanding the Least Common Multiple (LCM) of 6 and 10: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles unlocks a deeper appreciation for number theory and its applications in various fields. This comprehensive guide will not only show you how to calculate the LCM of 6 and 10 but also delve into the theoretical foundations, different calculation methods, and real-world applications. We'll explore multiple approaches, ensuring you grasp the concept thoroughly. Understanding LCM is crucial in areas like scheduling, measurement conversions, and even music theory!
Introduction to Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder. This concept is fundamental in mathematics and has practical implications across diverse fields. For example, finding the LCM helps determine the shortest time interval when two cyclical events will coincide.
Let's focus on our specific example: finding the LCM of 6 and 10. This seemingly simple problem offers a great opportunity to explore different methods for calculating the LCM, solidifying your understanding of the concept.
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers, is to list the multiples of each number until you find the smallest common multiple.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, ...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, ...
By comparing the lists, we can see that the smallest number present in both lists is 30. Therefore, the LCM of 6 and 10 is 30. This method is intuitive and easy to visualize, making it excellent for beginners. However, it becomes less efficient when dealing with larger numbers.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors. Prime factors are prime numbers that, when multiplied together, result in the original number.
- Prime factorization of 6: 2 x 3
- Prime factorization of 10: 2 x 5
To find the LCM using prime factorization, we identify the highest power of each prime factor present in the factorizations of both numbers.
- The prime factors involved are 2, 3, and 5.
- The highest power of 2 is 2¹ (from both 6 and 10).
- The highest power of 3 is 3¹ (from 6).
- The highest power of 5 is 5¹ (from 10).
Now, multiply these highest powers together: 2 x 3 x 5 = 30. Therefore, the LCM of 6 and 10 is 30. This method is more systematic and less prone to errors, particularly when dealing with larger numbers or multiple numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. There's a formula that elegantly connects the LCM and GCD:
LCM(a, b) = (a x b) / GCD(a, b)
Let's find the GCD of 6 and 10 first. We can use the Euclidean algorithm for this:
- Divide the larger number (10) by the smaller number (6): 10 ÷ 6 = 1 with a remainder of 4.
- Replace the larger number with the smaller number (6) and the smaller number with the remainder (4): 6 ÷ 4 = 1 with a remainder of 2.
- Repeat: 4 ÷ 2 = 2 with a remainder of 0.
The last non-zero remainder is the GCD, which is 2.
Now, apply the formula:
LCM(6, 10) = (6 x 10) / 2 = 60 / 2 = 30
Therefore, the LCM of 6 and 10 is 30. This method is efficient and leverages the relationship between LCM and GCD, offering a powerful alternative calculation approach.
Method 4: Using a Venn Diagram (Visual Representation)
While not a direct calculation method, a Venn diagram provides a visual representation that helps understand the relationship between the factors of the numbers and how the LCM is constructed.
Draw two overlapping circles, one for the prime factors of 6 (2 and 3) and one for the prime factors of 10 (2 and 5). The overlapping section represents the common factor (2). To find the LCM, multiply all the unique factors, including the common factor only once: 2 x 3 x 5 = 30. This visual approach is great for understanding the concept intuitively, particularly for students who benefit from visual learning.
Understanding the Significance of LCM
The LCM is not just a theoretical concept; it has practical applications in various real-world scenarios:
-
Scheduling: Imagine two buses arrive at a bus stop. One bus arrives every 6 minutes, and the other every 10 minutes. The LCM (30 minutes) tells you how long you have to wait until both buses arrive simultaneously.
-
Measurement Conversions: Converting between different units of measurement often requires finding the LCM. For example, when working with fractions of different denominators, the LCM of the denominators becomes the common denominator needed for addition or subtraction.
-
Music Theory: The LCM plays a role in understanding musical intervals and harmonies. The LCM of the frequencies of different notes helps determine when they will resonate together harmoniously.
-
Project Management: In project scheduling, tasks with different durations can be synchronized using the LCM to find the shortest time frame when all tasks can be completed simultaneously.
Frequently Asked Questions (FAQ)
Q: What if I need to find the LCM of more than two numbers?
A: You can extend the prime factorization method or the GCD-based method to accommodate more than two numbers. For the prime factorization, consider all prime factors present in all the numbers and their highest powers. For the GCD method, you can find the GCD of the first two numbers, then the GCD of the result and the third number, and so on.
Q: Is there a situation where the LCM and GCD are the same?
A: Yes, this happens when the two numbers are the same. For example, the LCM and GCD of 5 and 5 are both 5.
Q: Can the LCM of two numbers ever be smaller than one of the numbers?
A: No. The LCM is always greater than or equal to the larger of the two numbers. It's the smallest common multiple, and it must be at least as large as the largest of the original numbers.
Q: Why is the prime factorization method considered more efficient for larger numbers?
A: The listing method becomes impractical for large numbers because the lists of multiples would become extremely long. Prime factorization breaks down the numbers into their fundamental building blocks, making the calculation more systematic and efficient, regardless of the size of the numbers involved.
Conclusion
Finding the least common multiple of 6 and 10, while seemingly simple, serves as a gateway to understanding a powerful mathematical concept with wide-ranging applications. We explored several methods – listing multiples, prime factorization, using the GCD, and even a visual representation using a Venn diagram. Each method offers unique insights and efficiency depending on the context and the numbers involved. Mastering the LCM enhances your mathematical skills and provides you with a valuable tool applicable across many disciplines, from scheduling to music theory. Remember the fundamental principle: the LCM is the smallest positive integer divisible by all the given numbers without a remainder. By understanding this principle and employing the appropriate methods, you can confidently tackle LCM problems of any complexity.
Latest Posts
Latest Posts
-
Greek Yogurt Calories 1 2 Cup
Sep 25, 2025
-
Oldest Sports Of The World
Sep 25, 2025
-
What Is The Opposite Of
Sep 25, 2025
-
Difference Between Stalactites And Stalagmites
Sep 25, 2025
-
How To Compute Price Elasticity
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 6 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.