2 3 X 2 1
straightsci
Sep 22, 2025 · 6 min read
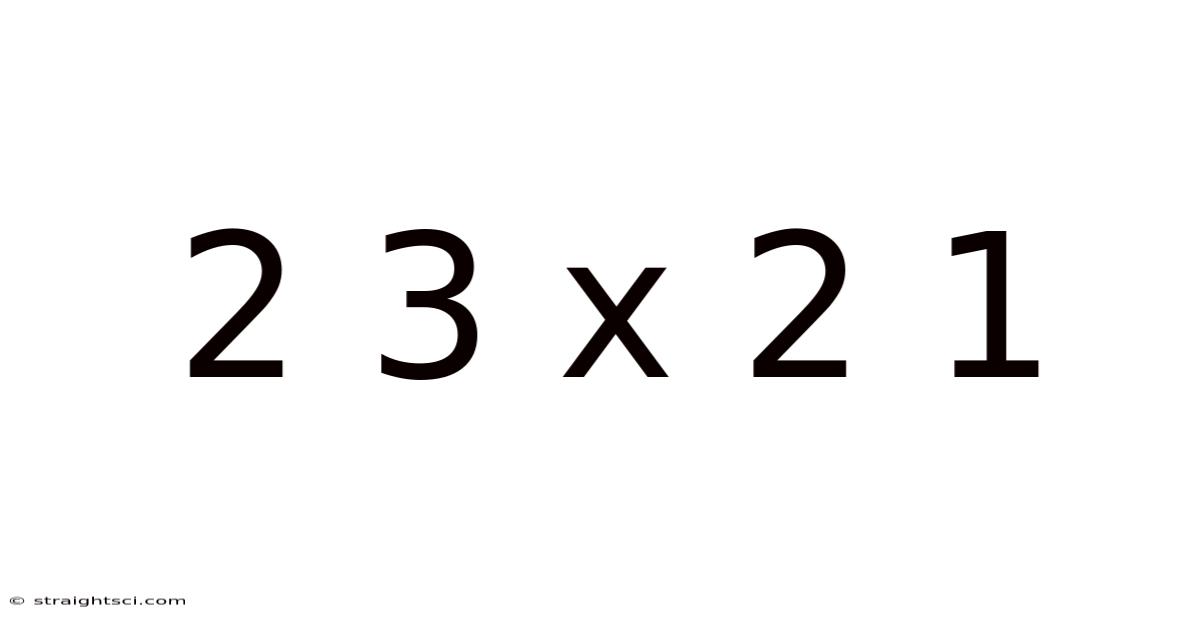
Table of Contents
Decoding 2 x 3 x 2 x 1: Exploring Factorials, Permutations, and Combinations
The seemingly simple expression "2 x 3 x 2 x 1" might appear innocuous at first glance. However, this sequence holds significant mathematical weight, representing fundamental concepts in combinatorics and probability theory. Understanding this expression unlocks the door to comprehending factorials, permutations, and combinations – vital tools used across various fields, from computer science and statistics to physics and finance. This article will delve into the meaning behind 2 x 3 x 2 x 1, exploring its mathematical significance and practical applications.
Introduction: What Does 2 x 3 x 2 x 1 Mean?
At its most basic level, 2 x 3 x 2 x 1 is simply a multiplication problem, resulting in the answer 12. But its true meaning lies beyond this straightforward calculation. This specific sequence represents the factorial of 3 (denoted as 3!), which is calculated as 3 x 2 x 1. The additional "2" at the beginning is crucial as it adds another dimension that links to permutations. It's in this context, understanding permutations and their relationship to factorials, where we unlock the deeper meaning of this seemingly straightforward equation.
Understanding Factorials: The Building Block
The cornerstone of understanding 2 x 3 x 2 x 1 is grasping the concept of a factorial. A factorial, denoted by an exclamation mark (!), is the product of all positive integers less than or equal to a given positive integer. For example:
- 1! = 1
- 2! = 2 x 1 = 2
- 3! = 3 x 2 x 1 = 6
- 4! = 4 x 3 x 2 x 1 = 24
- 5! = 5 x 4 x 3 x 2 x 1 = 120
And so on. Factorials grow rapidly; even relatively small numbers lead to large results. The factorial of zero (0!) is defined as 1, a convention essential for various mathematical formulas.
Permutations: Ordering Matters
Now let's introduce permutations. A permutation is an arrangement of objects in a specific order. Consider having 3 distinct objects (A, B, C). How many ways can you arrange these objects?
- ABC
- ACB
- BAC
- BCA
- CAB
- CBA
There are 6 possible arrangements. Notice that this number is equal to 3! (3 x 2 x 1 = 6). This is not a coincidence. The number of permutations of n distinct objects is n!.
Now, let's relate this back to our initial expression: 2 x 3 x 2 x 1. Imagine we have 3 distinct objects (A, B, C) and we want to choose 2 of them and arrange them in a specific order. This is where the "2" at the beginning of our expression comes into play.
Let's consider the possibilities:
- Selecting A and B: AB and BA (2 arrangements)
- Selecting A and C: AC and CA (2 arrangements)
- Selecting B and C: BC and CB (2 arrangements)
In total, there are 6 arrangements (2 x 3 = 6). This matches 3! If we instead wanted to choose all three, the calculation would be 3! (3 x 2 x 1 = 6). If we want to arrange only two items, the logic remains consistent; for choosing 2 out of 3 objects, we have:
- First position: 3 choices
- Second position: 2 choices (one already chosen)
Hence, 3 x 2 = 6 permutations. This is a simpler way to understand that the 2 x 3 x 2 x 1 expression might arise in the calculation of the number of permutations depending on the number of items selected from a given set.
Combinations: Order Doesn't Matter
Combinations differ from permutations; the order of the selected objects does not matter. Using the same example of 3 objects (A, B, C) and choosing 2, the combinations are:
- {A, B}
- {A, C}
- {B, C}
There are only 3 combinations. The formula for calculating the number of combinations of choosing k objects from a set of n objects is given by the binomial coefficient:
nCk = n! / (k! * (n-k)!)
In our example, choosing 2 objects from a set of 3:
3C2 = 3! / (2! * 1!) = (3 x 2 x 1) / ((2 x 1) x 1) = 3
This highlights the distinction between permutations (order matters) and combinations (order doesn't matter). The initial expression, 2 x 3 x 2 x 1, doesn't directly represent a combination calculation in a simple manner, unlike the permutations. It's primarily connected to permutations, particularly when selecting a subset and then arranging the selected elements.
Mathematical Applications and Real-World Examples
The concepts of factorials, permutations, and combinations have far-reaching implications across various disciplines:
-
Probability Theory: Calculating probabilities of events often involves permutations and combinations. For example, finding the probability of drawing specific cards from a deck of cards.
-
Computer Science: Algorithms involving sorting, searching, and scheduling often use factorial calculations to estimate the computational complexity.
-
Statistics: Statistical analysis frequently employs combinations to calculate probabilities associated with sample spaces.
-
Cryptography: Permutations play a critical role in creating secure encryption algorithms.
-
Genetics: In genetics, combinations help determine the possible gene combinations in offspring.
-
Sports: Calculating the number of possible ways teams can finish a tournament.
Beyond the Basics: Extending the Concept
While 2 x 3 x 2 x 1 highlights core concepts, more complex scenarios exist:
-
Permutations with repetitions: If objects are not distinct, the calculation becomes more intricate.
-
Circular permutations: Arranging objects in a circle changes the counting logic.
-
Multiset permutations: If objects can be selected multiple times, the counting methods differ.
Frequently Asked Questions (FAQ)
Q1: What is the difference between a permutation and a combination?
A permutation is an arrangement where order matters, while a combination is a selection where order doesn't matter. For example, arranging letters (permutation) is different from selecting a group of letters (combination).
Q2: Why is 0! defined as 1?
Defining 0! as 1 is a mathematical convention necessary for consistency in various formulas, including the binomial theorem and other combinatorial identities.
Q3: How can I calculate large factorials?
For large numbers, calculators or programming languages with mathematical libraries are essential. The values grow rapidly, making manual calculation impractical.
Q4: Are there any online tools to calculate permutations and combinations?
Yes, many online calculators and software packages can compute permutations and combinations efficiently.
Q5: How does the expression 2 x 3 x 2 x 1 relate to the concept of arrangements?
The expression arises when considering scenarios involving selecting a subset of elements and arranging those selected elements. The first "2" in the sequence might represent the number of options in a given step, followed by other factors representing successive choices with diminishing available options.
Conclusion: Unlocking the Power of Combinatorics
The seemingly simple expression "2 x 3 x 2 x 1" acts as a gateway to the fascinating world of combinatorics. Understanding factorials, permutations, and combinations is crucial for solving a wide variety of problems across diverse fields. While the numerical result is 12, the mathematical significance extends far beyond this simple calculation, emphasizing the importance of order, selection, and arrangement in problem-solving. By mastering these fundamental concepts, you equip yourself with powerful tools for tackling complex problems and gaining deeper insights into probability, statistics, and the underlying structure of many real-world phenomena.
Latest Posts
Latest Posts
-
Which Continent Is Mexico In
Sep 22, 2025
-
2 2 X 3 3
Sep 22, 2025
-
75 Kg How Many Pounds
Sep 22, 2025
-
Organs In Quadrants Of Abdomen
Sep 22, 2025
-
Convert 68 Kg To Pounds
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 2 3 X 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.