2 2 X 3 3
straightsci
Sep 22, 2025 · 6 min read
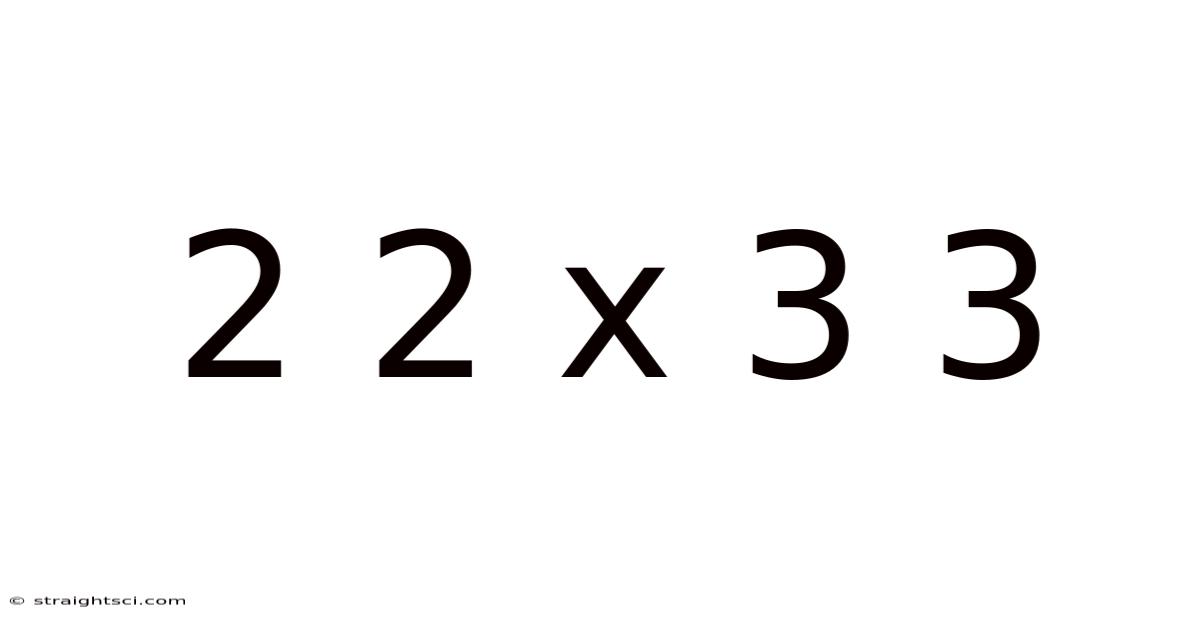
Table of Contents
Decoding 2 x 2 x 3 x 3: A Deep Dive into Multiplication, Factorization, and Beyond
This article explores the seemingly simple mathematical expression "2 x 2 x 3 x 3," delving far beyond the immediate answer to uncover the underlying principles of multiplication, factorization, prime numbers, and their applications in various mathematical fields. Understanding this seemingly basic calculation unlocks a door to more complex mathematical concepts. We'll examine its solutions, explore its factors, and discuss its significance in algebra, number theory, and even computer science.
Introduction: More Than Just a Calculation
At first glance, 2 x 2 x 3 x 3 appears to be a straightforward multiplication problem. The answer, 36, is easily obtained through sequential multiplication. However, this simple expression provides a fertile ground for exploring several fundamental mathematical concepts. This article will guide you through a detailed analysis, moving from the basic calculation to more advanced mathematical ideas related to prime factorization, exponents, and their real-world implications.
Step-by-Step Calculation: Finding the Answer
The simplest approach to solving 2 x 2 x 3 x 3 is through sequential multiplication:
- 2 x 2 = 4
- 4 x 3 = 12
- 12 x 3 = 36
Therefore, the solution to 2 x 2 x 3 x 3 is 36. This basic calculation forms the foundation for understanding the more complex concepts explored later.
Prime Factorization: Unveiling the Building Blocks
A key concept related to 2 x 2 x 3 x 3 is prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors – numbers divisible only by 1 and themselves. In our case:
- 2 is a prime number.
- 3 is a prime number.
The prime factorization of 36 is therefore 2 x 2 x 3 x 3, or more concisely, 2² x 3². This representation reveals the fundamental building blocks of the number 36. Understanding prime factorization is crucial in various areas of mathematics, including cryptography and number theory. It provides a unique and irreplaceable representation of any given integer.
Exponents and Powers: A Concise Representation
The prime factorization of 36, written as 2² x 3², utilizes exponents. Exponents (or powers) provide a shorthand way to represent repeated multiplication. The expression "2²" signifies 2 multiplied by itself twice (2 x 2), and "3²" represents 3 multiplied by itself twice (3 x 3). The use of exponents is not only more concise but also essential in more advanced algebraic manipulations and calculations.
Applications in Algebra: Expanding and Factoring Expressions
The concepts explored above are fundamental to algebraic manipulations. Consider the following algebraic expression:
(2x + 3y)(2x + 3y)
This expression, when expanded using the FOIL method (First, Outer, Inner, Last), results in:
4x² + 12xy + 9y²
Notice the similarity between the numerical coefficients in this expansion (4, 12, 9) and the original expression 2 x 2 x 3 x 3 = 36. The principles of multiplication and factorization are critical for simplifying, expanding, and solving algebraic equations. This seemingly simple numerical example highlights the interconnectedness of arithmetic and algebra.
Number Theory: Exploring the Properties of Numbers
Number theory, a branch of mathematics dedicated to studying the properties of numbers, relies heavily on concepts like prime factorization. The prime factorization of 36 (2² x 3²) helps to determine various properties of the number 36, such as its divisors, its number of divisors, and its relationship to other numbers. For instance, knowing the prime factorization allows us to easily determine that 36 is a perfect square (6²), since it has an even exponent for all its prime factors. Further explorations in number theory could involve analyzing the number of divisors, identifying whether it's abundant, deficient, or perfect, and exploring its connections to other numbers in sequences or patterns.
Geometry and its Link to 36
The number 36 also appears in various geometric contexts. Consider a square with a side length of 6 units. Its area is calculated as 6 x 6 = 36 square units. This simple geometric example connects the number 36 to spatial concepts. Furthermore, a 6 x 6 grid contains 36 smaller squares, demonstrating another link between the number and geometry. This connection extends to more complex geometric shapes and problems, highlighting the multifaceted nature of mathematical concepts.
Applications in Computer Science: Data Structures and Algorithms
In computer science, understanding factorization and number theory is crucial for designing efficient algorithms and data structures. Cryptography, a critical aspect of cybersecurity, relies heavily on prime numbers and their properties. The difficulty in factoring large numbers into their prime components forms the basis of many encryption algorithms. While 36 itself is too small to be useful in cryptography, understanding its factorization exemplifies the core principles used in these sophisticated algorithms. This connection underscores the relevance of fundamental mathematical concepts in seemingly unrelated fields.
Beyond the Basics: Exploring Further Concepts
The exploration of 2 x 2 x 3 x 3 can be extended to delve into more advanced mathematical concepts:
- Modular Arithmetic: Exploring the remainders when 36 is divided by various numbers leads to modular arithmetic, a fundamental concept in cryptography and number theory.
- Combinatorics: The number 36 can appear in combinatorial problems related to arrangements and selections.
- Number Systems: Representing 36 in different number systems (binary, hexadecimal, etc.) introduces further complexities and demonstrates how the same quantity can be expressed in various forms.
Frequently Asked Questions (FAQ)
-
Q: What is the simplest way to calculate 2 x 2 x 3 x 3?
- A: The simplest way is through sequential multiplication: 2 x 2 = 4, then 4 x 3 = 12, and finally 12 x 3 = 36.
-
Q: What is the prime factorization of 36?
- A: The prime factorization of 36 is 2² x 3².
-
Q: Is 36 a perfect square?
- A: Yes, 36 is a perfect square because it is 6².
-
Q: What are some real-world applications of understanding prime factorization?
- A: Prime factorization is crucial in cryptography, where the difficulty of factoring large numbers is used to secure data. It also has applications in various areas of mathematics and computer science.
-
Q: How does this simple calculation relate to more advanced mathematical concepts?
- A: This simple calculation provides a foundation for understanding prime factorization, exponents, algebraic manipulations, number theory, and even applications in computer science and cryptography.
Conclusion: A Simple Expression with Profound Implications
The seemingly simple calculation 2 x 2 x 3 x 3 = 36 serves as a gateway to a vast world of mathematical concepts. From the basics of multiplication and prime factorization to the complexities of algebra, number theory, and computer science, this expression highlights the interconnectedness of mathematical ideas. By exploring this simple problem in depth, we gain a deeper appreciation for the elegance and power of mathematics, and the profound implications hidden within seemingly simple numerical expressions. The journey from a straightforward calculation to a comprehensive understanding of its implications demonstrates the enduring beauty and practical significance of mathematical exploration. The seemingly simple calculation, therefore, opens doors to a much wider and richer understanding of the mathematical world.
Latest Posts
Latest Posts
-
62 Kg Convert To Lbs
Sep 22, 2025
-
Definition Of The Spanish Inquisition
Sep 22, 2025
-
What Is And In Measurements
Sep 22, 2025
-
23kg Is How Many Pounds
Sep 22, 2025
-
How To Check Costco Inventory
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 2 2 X 3 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.