2/3 Cup + 2/3 Cup
straightsci
Sep 13, 2025 · 6 min read
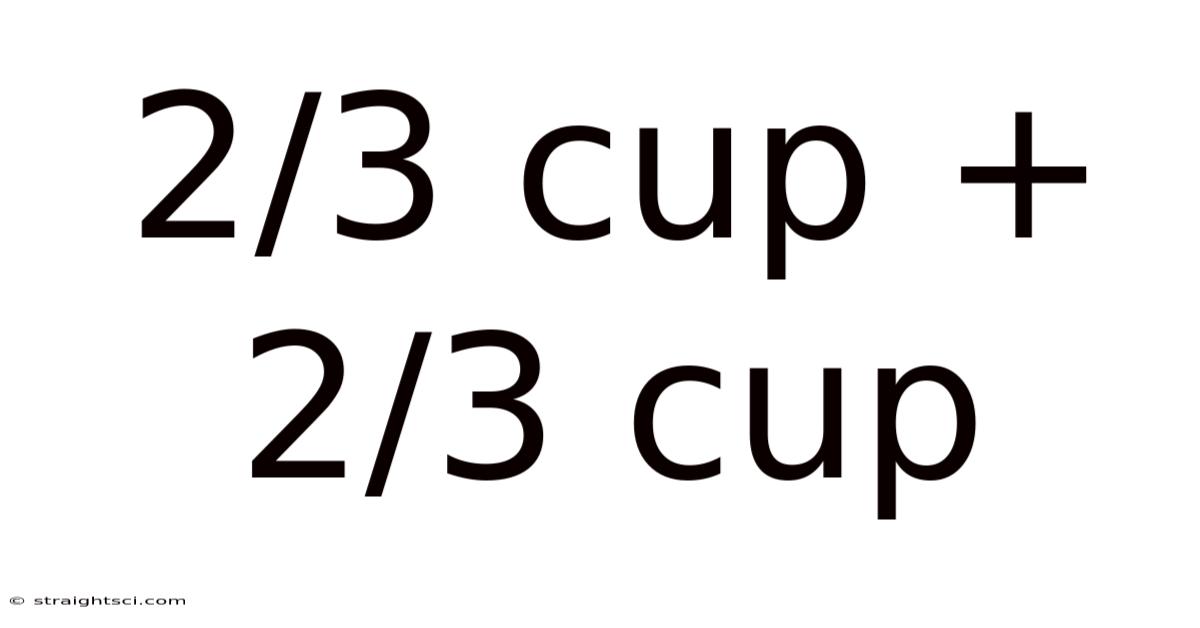
Table of Contents
Decoding the Simple Sum: 2/3 Cup + 2/3 Cup
Understanding fractions is a fundamental skill in mathematics, with applications extending far beyond the classroom. From baking a delicious cake to calculating medication dosages, fractional arithmetic is crucial in our daily lives. This article delves into the seemingly simple yet conceptually important addition of two-thirds of a cup plus two-thirds of a cup, exploring the mathematical process, real-world applications, and addressing common misconceptions. We'll go beyond just the answer and unravel the underlying principles that make this calculation so significant.
Introduction: Why This Matters More Than You Think
The question, "What is 2/3 cup + 2/3 cup?" might seem trivial at first glance. However, mastering this type of calculation forms the bedrock for understanding more complex mathematical concepts. It's a stepping stone to understanding fractions, addition, and even more advanced topics like algebra and calculus. The ability to accurately measure and add fractions is crucial in various fields, including:
- Cooking and Baking: Recipes often rely on precise measurements, and incorrectly adding fractions can lead to disastrous results.
- Science and Engineering: Many scientific experiments and engineering projects necessitate precise measurements and calculations involving fractions.
- Medicine: Accurate medication dosages are critical, and pharmacists and doctors must be adept at working with fractions.
- Construction and Carpentry: Precise measurements are fundamental in construction and carpentry, ensuring the structural integrity of buildings and other structures.
Adding Fractions: A Step-by-Step Guide
Adding fractions might seem daunting, but with a systematic approach, it becomes straightforward. Let's break down the addition of 2/3 cup + 2/3 cup:
1. Identify the Common Denominator: In this case, both fractions have the same denominator, 3. This simplifies the process considerably. If the denominators were different, we would need to find a least common multiple (LCM) to create a common denominator before adding the fractions.
2. Add the Numerators: Since the denominators are the same, we simply add the numerators: 2 + 2 = 4.
3. Keep the Denominator the Same: The denominator remains unchanged, so we maintain the denominator as 3.
4. Simplify the Result: This gives us the fraction 4/3. However, this is an improper fraction (where the numerator is larger than the denominator). To convert it to a mixed number (a whole number and a fraction), we divide the numerator (4) by the denominator (3):
4 ÷ 3 = 1 with a remainder of 1.
Therefore, 4/3 is equivalent to 1 and 1/3.
Therefore, 2/3 cup + 2/3 cup = 1 and 1/3 cups.
Visualizing the Sum: A Practical Approach
Sometimes, visualizing the problem can make it easier to understand. Imagine two measuring cups, each filled with 2/3 of a cup of flour. If you pour the contents of both cups into a larger container, you'll have a total of 1 and 1/3 cups of flour. This visual representation reinforces the mathematical calculation. You can also use diagrams, like dividing a circle into thirds and shading in two-thirds for each fraction, and then combining them to see the resulting whole and one-third.
Understanding Improper Fractions and Mixed Numbers
The concept of improper fractions and mixed numbers is crucial in fraction arithmetic. An improper fraction has a numerator larger than or equal to its denominator (e.g., 4/3, 7/5). A mixed number combines a whole number and a proper fraction (e.g., 1 and 1/3, 2 and 2/5). Knowing how to convert between these two forms is essential for accurate calculations and understanding the magnitude of the fraction.
Expanding the Concept: Adding Fractions with Different Denominators
While the example of 2/3 cup + 2/3 cup simplifies the process, let's explore how to add fractions with different denominators. For instance, consider 1/2 cup + 1/3 cup.
1. Find the Least Common Multiple (LCM): The LCM of 2 and 3 is 6. This will be our common denominator.
2. Convert the Fractions: We need to convert both fractions to have a denominator of 6.
- 1/2 becomes 3/6 (multiply both numerator and denominator by 3)
- 1/3 becomes 2/6 (multiply both numerator and denominator by 2)
3. Add the Numerators: 3/6 + 2/6 = 5/6
Therefore, 1/2 cup + 1/3 cup = 5/6 cup.
Real-World Applications: Beyond the Classroom
The ability to add fractions isn't confined to theoretical mathematical problems. It's a crucial skill in numerous practical situations:
- Baking a Double Batch: If a recipe calls for 2/3 cup of sugar, and you want to double the recipe, you'll need to add 2/3 cup + 2/3 cup = 1 and 1/3 cups of sugar.
- Building a Fence: If each section of a fence requires 2/3 of a meter of wood, and you need two sections, you'll need 1 and 1/3 meters of wood.
- Mixing Medications: Although highly specialized and requiring professional training, the principles of adding fractions are applied in calculating accurate medication dosages.
- Sewing Projects: Many sewing projects require precise measurements of fabric, often involving fractions of an inch or centimeter.
Frequently Asked Questions (FAQ)
Q: What if the fractions had different denominators?
A: If the fractions had different denominators, you would need to find the least common multiple (LCM) of the denominators and convert the fractions to equivalent fractions with the same denominator before adding the numerators.
Q: Why do we need to simplify fractions?
A: Simplifying fractions makes the result easier to understand and use. An improper fraction like 4/3 is less intuitive than the mixed number 1 and 1/3. Simplified fractions also make further calculations simpler.
Q: Can I use a calculator to add fractions?
A: Many calculators can add fractions, but understanding the underlying mathematical principles is crucial for solving more complex problems and developing a strong foundation in mathematics.
Conclusion: Mastering Fractions – A Foundation for Success
The seemingly simple addition of 2/3 cup + 2/3 cup provides a valuable gateway to understanding fractions and their applications in various aspects of life. By mastering this fundamental concept, you build a strong foundation for more advanced mathematical concepts and enhance your ability to solve real-world problems involving measurement, calculation, and precise quantities. Remember to practice regularly and don't be afraid to visualize the problem to gain a deeper understanding. The ability to confidently manipulate fractions is a valuable asset that will serve you well throughout your academic and professional endeavors. This skill transcends simple arithmetic; it's a key to unlocking a deeper understanding of the world around us, one fraction at a time.
Latest Posts
Latest Posts
-
Phosphorus Protons Electrons And Neutrons
Sep 13, 2025
-
Example Of An Illusory Correlation
Sep 13, 2025
-
Small Caps Effect In Word
Sep 13, 2025
-
Star Format For Answering Questions
Sep 13, 2025
-
Why Is The Defibrillation Important
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 2/3 Cup + 2/3 Cup . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.