1 Tan 2x Sec 2x
straightsci
Sep 12, 2025 · 5 min read
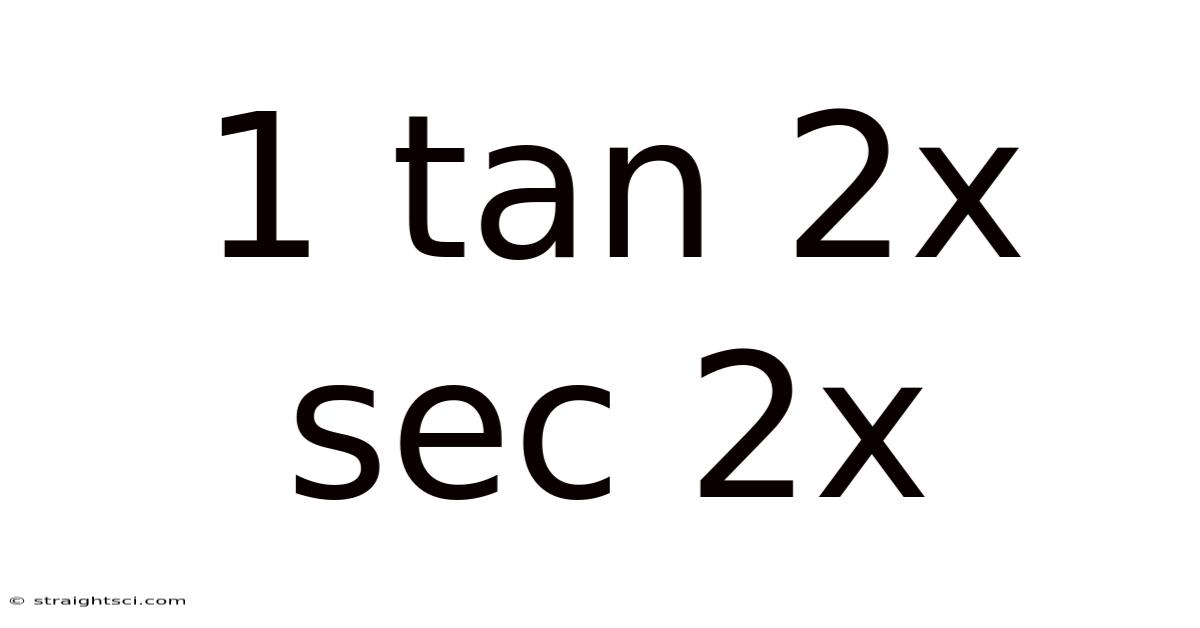
Table of Contents
Decoding the Trigonometric Identity: 1 + tan²x = sec²x and its Application to 1 + tan²(2x) = sec²(2x)
Understanding trigonometric identities is crucial for anyone studying mathematics, particularly in calculus, physics, and engineering. This article delves into the fundamental identity 1 + tan²x = sec²x and its extension to 1 + tan²(2x) = sec²(2x), providing a comprehensive explanation, detailed proofs, and practical applications. We'll explore how this identity simplifies complex trigonometric expressions and enhances problem-solving skills.
Introduction: The Pythagorean Identity and its Variations
The core of this exploration lies in the Pythagorean identity: sin²x + cos²x = 1. This foundational identity, a direct consequence of the Pythagorean theorem applied to a unit circle, forms the basis for numerous other trigonometric relationships. By dividing this identity by cos²x, we derive:
1 + tan²x = sec²x
Where:
- tan x = sin x / cos x (tangent of x)
- sec x = 1 / cos x (secant of x)
This identity provides a powerful tool for simplifying expressions involving tangents and secants. Similarly, replacing 'x' with '2x' directly leads us to:
1 + tan²(2x) = sec²(2x)
This seemingly simple substitution opens up a world of possibilities in simplifying more complex trigonometric expressions and solving trigonometric equations. Let's now delve deeper into proving these identities and exploring their applications.
Proof of 1 + tan²x = sec²x
We can prove this identity directly from the fundamental Pythagorean identity:
-
Start with the Pythagorean Identity: sin²x + cos²x = 1
-
Divide by cos²x: (sin²x + cos²x) / cos²x = 1 / cos²x
-
Separate the fractions: sin²x / cos²x + cos²x / cos²x = 1 / cos²x
-
Simplify using definitions of tan x and sec x: tan²x + 1 = sec²x
-
Rearrange for the desired form: 1 + tan²x = sec²x
This concise proof demonstrates the direct link between the Pythagorean identity and the tangent-secant identity. The elegance of this derivation highlights the interconnectedness of trigonometric functions.
Proof of 1 + tan²(2x) = sec²(2x)
The proof for 1 + tan²(2x) = sec²(2x) follows the same principle, but utilizes the double-angle formulas for sine and cosine. Recall the double-angle formulas:
- sin(2x) = 2sin(x)cos(x)
- cos(2x) = cos²(x) - sin²(x) = 2cos²(x) - 1 = 1 - 2sin²(x)
Now let's proceed with the proof:
-
Start with the Pythagorean Identity (for 2x): sin²(2x) + cos²(2x) = 1
-
Divide by cos²(2x): (sin²(2x) + cos²(2x)) / cos²(2x) = 1 / cos²(2x)
-
Separate the fractions: sin²(2x) / cos²(2x) + cos²(2x) / cos²(2x) = 1 / cos²(2x)
-
Simplify using definitions of tan(2x) and sec(2x): tan²(2x) + 1 = sec²(2x)
-
Rearrange for the desired form: 1 + tan²(2x) = sec²(2x)
This proof effectively demonstrates that the identity holds true for the double angle as well, reinforcing the generality of the relationship between tangent and secant functions.
Applications and Problem Solving
The identities 1 + tan²x = sec²x and 1 + tan²(2x) = sec²(2x) are invaluable tools for simplifying complex trigonometric expressions. They allow us to:
-
Simplify expressions: Transform expressions containing both tangents and secants into simpler forms, often involving only one trigonometric function. This simplifies calculations and makes it easier to solve equations.
-
Solve trigonometric equations: These identities can be used to rewrite equations in a more manageable form, enabling the solution of otherwise intractable equations.
-
Integrate and differentiate trigonometric functions: In calculus, these identities are often crucial for simplifying integrals and derivatives involving trigonometric functions, leading to more efficient solutions.
Let's look at a few examples:
Example 1: Simplifying a Trigonometric Expression
Simplify the expression: (sec²x)(1 - sin²x) - tan²x
Using the identities:
- sec²x = 1 + tan²x
- 1 - sin²x = cos²x
We can rewrite the expression as:
(1 + tan²x)(cos²x) - tan²x = cos²x + tan²x(cos²x) - tan²x
Since tan x = sin x / cos x, tan²x = sin²x / cos²x
= cos²x + sin²x - tan²x = 1 - tan²x
This significantly simplifies the original expression.
Example 2: Solving a Trigonometric Equation
Solve the equation: 2tan²x + sec²x = 3
Substituting sec²x = 1 + tan²x, we get:
2tan²x + 1 + tan²x = 3
3tan²x = 2
tan²x = 2/3
tan x = ±√(2/3)
This allows us to find the solutions for x.
Extending the Identity to Other Angles: Generalization
The principle underlying 1 + tan²x = sec²x extends beyond the double angle (2x). The identity holds true for any angle, including multiples of x (3x, 4x, etc.) and for angles expressed in radians or degrees. The underlying principle is always the same: it's a direct consequence of the Pythagorean identity applied to the relevant trigonometric functions.
Frequently Asked Questions (FAQ)
-
Q: Are these identities only valid for certain values of x?
- A: No, these identities are valid for all values of x for which the trigonometric functions are defined (i.e., where cos x ≠ 0, and cos(2x) ≠ 0). Points where cosine is zero are considered vertical asymptotes for tangent and secant, and thus the equations are undefined at these points.
-
Q: Can I use these identities to solve any trigonometric equation?
- A: While these identities are incredibly useful, they are not a universal solution for all trigonometric equations. They are most helpful when dealing with expressions involving tangents and secants.
-
Q: How do these identities relate to other trigonometric identities?
- A: These identities are directly derived from the fundamental Pythagorean identity (sin²x + cos²x = 1), making them an integral part of the broader network of trigonometric relationships.
-
Q: Are there similar identities for other trigonometric functions?
- A: Yes, by dividing the Pythagorean identity by sin²x, we obtain 1 + cot²x = csc²x, showcasing a similar relationship between cotangent and cosecant.
Conclusion: Mastering Trigonometric Identities for Enhanced Problem Solving
The identities 1 + tan²x = sec²x and 1 + tan²(2x) = sec²(2x) are fundamental tools in the study of trigonometry and its applications. Understanding their derivations and applying them effectively simplifies complex expressions, solves intricate equations, and enhances proficiency in calculus and related fields. By mastering these identities, you'll gain a deeper appreciation for the elegance and power of trigonometric relationships and their importance in various scientific and engineering disciplines. Remember to practice regularly with different types of problems to solidify your understanding and build confidence in using these vital trigonometric identities. Through consistent effort and application, you will unlock the full potential of these powerful tools in simplifying and solving trigonometric problems.
Latest Posts
Latest Posts
-
Equation For Kelvin To Celsius
Sep 12, 2025
-
190 Degrees Farenheit To Celcius
Sep 12, 2025
-
Is 1 4 Bigger Than 3 4
Sep 12, 2025
-
Pick A Number Between 1 20
Sep 12, 2025
-
55 Kg Convert To Lbs
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 1 Tan 2x Sec 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.