1 4 Divided By 4
straightsci
Sep 02, 2025 · 6 min read
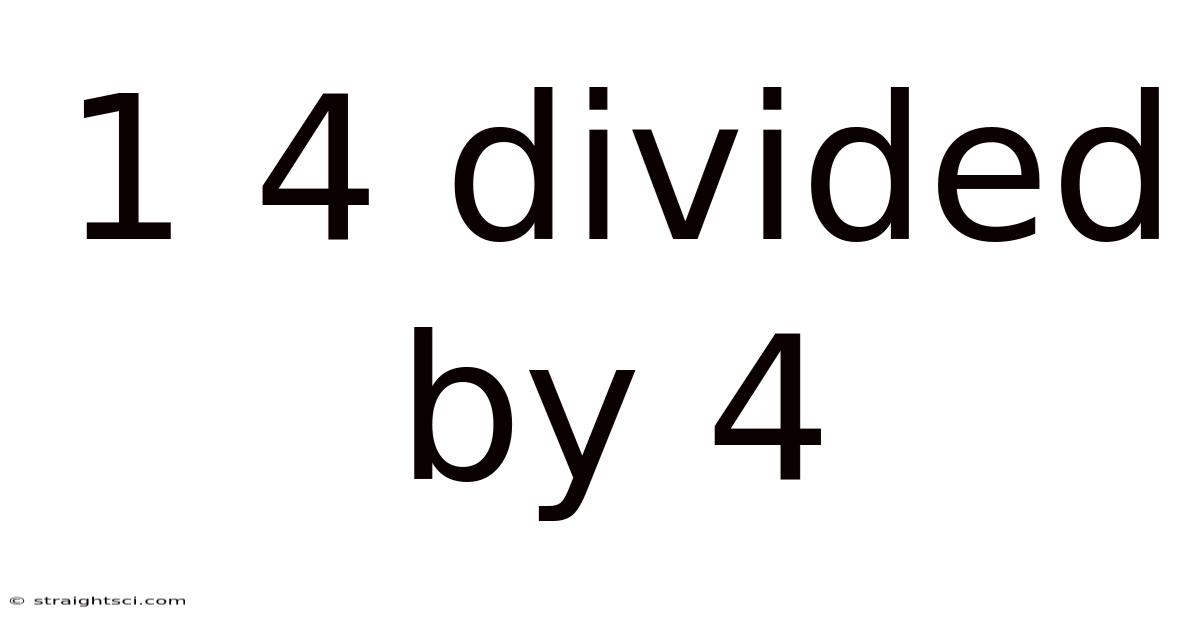
Table of Contents
Decoding 1/4 Divided by 4: A Deep Dive into Fraction Division
Understanding fraction division can seem daunting at first, but with a clear, step-by-step approach, it becomes surprisingly straightforward. This article will guide you through the process of solving 1/4 divided by 4, explaining the underlying principles and providing you with a solid foundation for tackling more complex fraction division problems. We'll cover various methods, ensuring you grasp the concept thoroughly, and delve into the practical applications of this seemingly simple calculation. This comprehensive guide will equip you with the skills to confidently approach any fraction division problem you encounter.
Introduction: Why Understanding Fraction Division Matters
Fractions are fundamental building blocks in mathematics, representing parts of a whole. The ability to divide fractions is crucial for various applications, ranging from simple everyday tasks like splitting a recipe to complex engineering calculations. Mastering this skill is essential for success in algebra, calculus, and numerous other fields. This seemingly simple problem, 1/4 divided by 4, serves as an excellent starting point to understand the core principles of fraction division. We will explore not just the how, but also the why behind the process, providing you with a solid conceptual understanding.
Method 1: The "Keep, Change, Flip" Method
This is perhaps the most popular and easily remembered method for dividing fractions. It's a shortcut that simplifies the process significantly. Let's break it down:
-
Keep: Keep the first fraction exactly as it is. In our case, this remains 1/4.
-
Change: Change the division sign (÷) to a multiplication sign (×).
-
Flip: Flip the second fraction (the divisor). Since 4 can be written as 4/1, flipping it gives us 1/4.
So, our problem transforms from (1/4) ÷ 4 to (1/4) × (1/4).
-
Multiply: Now, we simply multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(1 × 1) / (4 × 4) = 1/16
Therefore, 1/4 divided by 4 equals 1/16.
Method 2: The Common Denominator Method
This method emphasizes the underlying principle of division as the inverse of multiplication. We can rewrite the problem as finding a number which, when multiplied by 4, equals 1/4.
-
Convert to a Common Denominator: The easiest way to do this is to rewrite 4 as a fraction with a denominator of 4: 4/1 becomes 16/4.
-
Solve the Equation: Now our equation looks like this: x * 16/4 = 1/4
-
Isolate x: To isolate 'x', we multiply both sides of the equation by the reciprocal of 16/4, which is 4/16 (or simplified to 1/4):
(1/4) * (4/16) * (16/4) = (1/4) * (4/16)
This simplifies to: x = 1/16
Therefore, again, we arrive at the answer: 1/16.
Method 3: Visual Representation
Visualizing the problem can greatly enhance understanding. Imagine a pizza cut into four equal slices (quarters). 1/4 represents one of these slices. Dividing this slice into four equal parts would mean each smaller piece represents 1/16 of the whole pizza. This visual representation provides a concrete understanding of the abstract concept of fraction division.
Explanation of the Mathematical Principles
The success of both the "Keep, Change, Flip" method and the common denominator method hinges on the fundamental concept of reciprocals. The reciprocal of a number is simply 1 divided by that number. For example, the reciprocal of 4 is 1/4, and the reciprocal of 1/4 is 4.
When we divide by a fraction, we're essentially multiplying by its reciprocal. This is why the "Keep, Change, Flip" method works. We change the division to multiplication and use the reciprocal of the second fraction. The common denominator method achieves the same result by manipulating the fractions to find a solution that satisfies the division equation.
This concept applies universally to all fraction division problems. Regardless of the complexity of the fractions, the principle of using the reciprocal remains constant.
Applications of Fraction Division in Real Life
Fraction division isn't just a theoretical concept; it has numerous practical applications. Here are a few examples:
-
Cooking: If a recipe calls for 1/4 cup of flour and you want to make only 1/4 of the recipe, you would need to divide 1/4 by 4 to find the amount of flour required (1/16 cup).
-
Sewing: Dividing fabric into equal parts for a project often involves fractions.
-
Construction: Accurate measurements in construction projects frequently necessitate dividing fractions.
-
Data Analysis: Many data analysis tasks involve working with fractions and understanding their relationships through division.
Frequently Asked Questions (FAQ)
-
Why does the "Keep, Change, Flip" method work? It works because dividing by a fraction is equivalent to multiplying by its reciprocal. This is a fundamental property of fractions.
-
Can I use this method for dividing any fractions? Yes, absolutely. The "Keep, Change, Flip" method is a universally applicable technique for dividing fractions.
-
What if the second number isn't a whole number? Treat the whole number as a fraction with a denominator of 1 (e.g., 4 becomes 4/1). Then apply the "Keep, Change, Flip" method.
-
Is there a difference between dividing by 4 and multiplying by 1/4? No, they are mathematically equivalent. Dividing by a number is the same as multiplying by its reciprocal.
-
How can I check my answer? You can check your answer by multiplying the result (1/16) by the divisor (4). If you get the original dividend (1/4), your calculation is correct.
Conclusion: Mastering Fraction Division for Future Success
Mastering the skill of fraction division, even something as seemingly simple as 1/4 divided by 4, is a crucial step in building a strong foundation in mathematics. This article has demonstrated different methods for solving such problems, emphasizing the underlying mathematical principles. The practical applications of this skill extend far beyond the classroom, making it a valuable tool for various aspects of life. Remember the "Keep, Change, Flip" method as a quick and easy approach, but also understand the underlying concepts of reciprocals and the common denominator method to solidify your understanding. With consistent practice, you'll become confident and proficient in tackling any fraction division problem. Remember that understanding the why behind the methods is just as important as understanding the how. By grasping these fundamentals, you'll not just solve problems, but you'll truly understand the mathematical language at play. This comprehensive understanding will serve you well in your future mathematical endeavors.
Latest Posts
Latest Posts
-
Longest Running Musical In Broadway
Sep 02, 2025
-
Is Miles Longer Than Kilometers
Sep 02, 2025
-
What Is A Couplet Poem
Sep 02, 2025
-
L C M Of 8 And 10
Sep 02, 2025
-
1 2 A Pint In Cups
Sep 02, 2025
Related Post
Thank you for visiting our website which covers about 1 4 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.