L.c.m Of 8 And 10
straightsci
Sep 02, 2025 · 6 min read
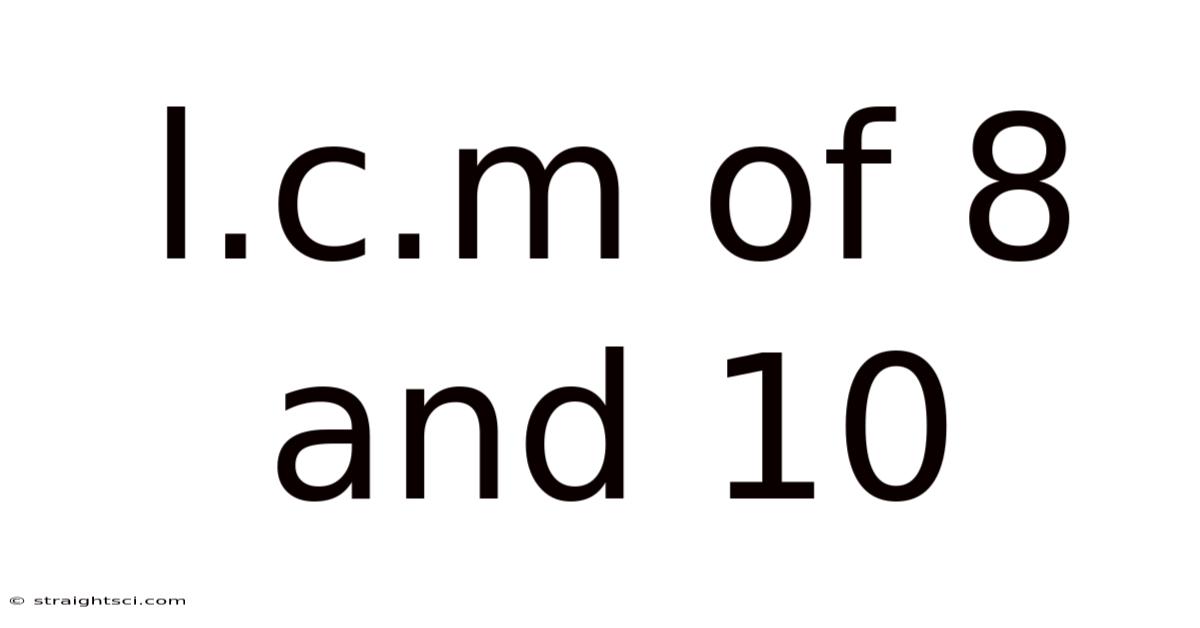
Table of Contents
Unveiling the Secrets of LCM: A Deep Dive into the Least Common Multiple of 8 and 10
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts opens doors to a deeper appreciation of number theory and its applications in various fields. This article delves into the LCM of 8 and 10, providing a comprehensive explanation suitable for learners of all levels. We'll explore different methods for calculating the LCM, unravel the theoretical underpinnings, and showcase the practical relevance of this seemingly basic concept. By the end, you’ll not only know the LCM of 8 and 10 but also possess a solid understanding of how to tackle similar problems and appreciate the broader mathematical context.
Introduction to Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the given numbers as factors. This concept is fundamental in various mathematical operations, from simplifying fractions to solving problems in algebra and beyond. Understanding the LCM is crucial in fields like scheduling, music theory, and even computer science. In this article, our focus is on finding the LCM of 8 and 10, but the methods explained can be applied to any set of integers.
Method 1: Listing Multiples
The most straightforward method for finding the LCM of small numbers is by listing the multiples of each number until a common multiple is found. Let’s apply this to 8 and 10:
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 96, ...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, ...
By comparing the two lists, we can see that the smallest number appearing in both lists is 40. Therefore, the LCM of 8 and 10 is 40. This method is simple and intuitive, especially for smaller numbers, but it can become cumbersome and time-consuming for larger numbers.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, involves using prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors. Let's break down 8 and 10 into their prime factors:
- 8 = 2 x 2 x 2 = 2³
- 10 = 2 x 5
To find the LCM using prime factorization, we identify the highest power of each prime factor present in the numbers:
- The highest power of 2 is 2³ = 8
- The highest power of 5 is 5¹ = 5
Now, multiply these highest powers together: 8 x 5 = 40. Therefore, the LCM of 8 and 10 is 40. This method is more systematic and efficient than listing multiples, especially when dealing with larger numbers or multiple numbers.
Method 3: Greatest Common Divisor (GCD) and LCM Relationship
The greatest common divisor (GCD) and the least common multiple (LCM) are intimately related. There's a neat formula connecting them:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
First, let's find the GCD of 8 and 10 using the Euclidean algorithm:
- Divide the larger number (10) by the smaller number (8): 10 ÷ 8 = 1 with a remainder of 2.
- Replace the larger number with the smaller number (8) and the smaller number with the remainder (2): 8 ÷ 2 = 4 with a remainder of 0.
- The last non-zero remainder is the GCD. Therefore, GCD(8, 10) = 2.
Now, we can use the formula:
LCM(8, 10) x GCD(8, 10) = 8 x 10 LCM(8, 10) x 2 = 80 LCM(8, 10) = 80 ÷ 2 = 40
This method confirms that the LCM of 8 and 10 is indeed 40. This approach is particularly useful when dealing with larger numbers, as finding the GCD is often easier than directly calculating the LCM.
Visual Representation: Venn Diagrams
A visual approach using Venn diagrams can enhance our understanding of GCD and LCM. Represent the prime factors of each number in separate circles. The overlapping section represents the GCD, while the entire area represents the LCM.
For 8 (2 x 2 x 2) and 10 (2 x 5):
- Overlapping section (GCD): One '2' (representing GCD = 2)
- Entire area (LCM): Three '2's and one '5' (representing LCM = 2 x 2 x 2 x 5 = 40)
This visualization clearly illustrates the relationship between the prime factors, GCD, and LCM.
Applications of LCM
The LCM has numerous applications across various disciplines:
- Scheduling: Imagine two buses arrive at a bus stop, one every 8 minutes and the other every 10 minutes. The LCM (40) tells us when both buses will arrive simultaneously again.
- Fraction Arithmetic: Finding the LCM of the denominators is essential when adding or subtracting fractions. This allows us to find a common denominator for easier calculation.
- Music Theory: The LCM helps determine the least common period of musical rhythms.
- Computer Science: In tasks involving cyclic processes or repeating patterns, the LCM plays a vital role in synchronization and optimization.
Further Exploration: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For instance, to find the LCM of 8, 10, and 12:
- Prime Factorization: 8 = 2³, 10 = 2 x 5, 12 = 2² x 3
- Highest Powers: The highest powers are 2³ = 8, 3¹ = 3, and 5¹ = 5.
- Multiplication: LCM(8, 10, 12) = 8 x 3 x 5 = 120
The LCM of 8, 10, and 12 is 120.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between LCM and GCD?
- A: The LCM is the smallest common multiple of two or more numbers, while the GCD is the greatest common divisor (largest common factor) of two or more numbers. They are inversely related.
-
Q: Can the LCM of two numbers be greater than their product?
- A: No, the LCM of two numbers will always be less than or equal to their product.
-
Q: Is there a formula to directly calculate the LCM without using prime factorization or the GCD?
- A: While there isn't a single, universally efficient formula that avoids prime factorization or the GCD relationship, iterative methods exist, but they are generally less efficient for larger numbers.
-
Q: Why is the LCM important in solving real-world problems?
- A: The LCM helps us determine cycles, coincidences, and common occurrences in various scenarios, making it crucial in scheduling, music, and even computer science for efficient resource management.
Conclusion
Understanding the least common multiple is more than just a mathematical exercise; it's a gateway to appreciating the fundamental principles of number theory and its far-reaching applications. This article has explored various methods for calculating the LCM, focusing on the LCM of 8 and 10 as a practical example. We've also examined the relationship between LCM and GCD and highlighted the practical relevance of this seemingly simple concept. Whether you're a student grappling with arithmetic or a professional applying mathematical principles to real-world challenges, a solid grasp of the LCM empowers you with a valuable tool for problem-solving and understanding the intricate beauty of numbers. Remember to choose the method best suited to the numbers involved, employing prime factorization for efficiency when dealing with larger numbers. The journey of understanding LCM is a continuous exploration, and with practice, mastering this concept will become second nature.
Latest Posts
Latest Posts
-
How Many Ounces In Ton
Sep 02, 2025
-
What Are Pure Substances Examples
Sep 02, 2025
-
Enthalpy Of Formation For Water
Sep 02, 2025
-
Confounding Variable Vs Extraneous Variable
Sep 02, 2025
-
How Many Yards In Kilometer
Sep 02, 2025
Related Post
Thank you for visiting our website which covers about L.c.m Of 8 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.