1/2 X 2/3 X 3/4
straightsci
Sep 12, 2025 · 5 min read
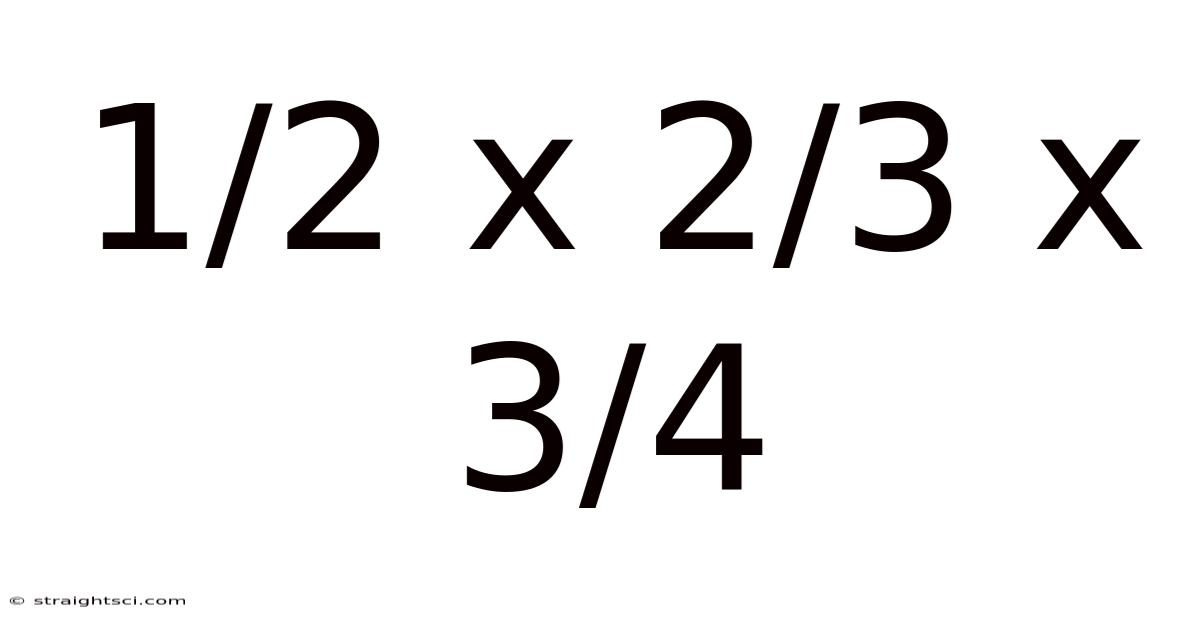
Table of Contents
Unveiling the Pattern: A Deep Dive into 1/2 x 2/3 x 3/4 and Beyond
This article explores the seemingly simple mathematical expression 1/2 x 2/3 x 3/4, delving far beyond the immediate calculation to uncover the underlying patterns, principles, and broader applications within mathematics. We'll unpack the solution, discuss the concept of multiplication of fractions, explore the possibility of extending this pattern to larger sequences, and finally, consider its implications in various mathematical contexts. This journey will equip you with a deeper understanding of fractions, sequences, and mathematical reasoning.
Understanding the Fundamentals: Multiplying Fractions
Before tackling the specific problem, let's refresh our understanding of fraction multiplication. Multiplying fractions is straightforward: you multiply the numerators (the top numbers) together and the denominators (the bottom numbers) together. For example, 1/2 multiplied by 2/3 is calculated as (1 x 2) / (2 x 3) = 2/6. This fraction can then be simplified by dividing both the numerator and the denominator by their greatest common divisor, which in this case is 2, resulting in 1/3.
Solving 1/2 x 2/3 x 3/4
Now, let's apply this knowledge to our specific problem: 1/2 x 2/3 x 3/4. Following the rules of fraction multiplication:
- Multiply the numerators: 1 x 2 x 3 = 6
- Multiply the denominators: 2 x 3 x 4 = 24
- Form the resulting fraction: 6/24
This fraction, 6/24, is not in its simplest form. To simplify, we find the greatest common divisor of 6 and 24, which is 6. Dividing both the numerator and the denominator by 6 gives us:
6/24 = 1/4
Therefore, the solution to 1/2 x 2/3 x 3/4 is 1/4.
Identifying Patterns and Extending the Sequence
The beauty of mathematics lies in its patterns. Let's examine the sequence we started with more closely. Notice anything interesting? We can rewrite the sequence as:
(1/2) * (2/3) * (3/4)
Observe the cancellation: The numerator of each fraction cancels with the denominator of the next. This leads to a significant simplification. If we extend this pattern, let's see what happens:
- 1/2 x 2/3 x 3/4 x 4/5: The numerators and denominators cancel out, leaving us with 1/5.
- 1/2 x 2/3 x 3/4 x 4/5 x 5/6: The pattern continues, resulting in 1/6.
We can generalize this pattern. If we have a sequence of fractions of the form:
(1/2) * (2/3) * (3/4) * ... * (n/(n+1))
The resulting fraction will always simplify to 1/(n+1). This is a powerful observation, illustrating the elegance and predictability of mathematical sequences.
Mathematical Concepts in Action: Telescoping Product
The cancellation we observed is a classic example of a telescoping product. This is a mathematical technique where consecutive terms in a product cancel out, leaving only a few terms at the beginning and end. This simplification dramatically reduces the complexity of calculations, revealing underlying patterns that might otherwise be obscured. Telescoping products are frequently encountered in calculus and other advanced mathematical areas. Understanding this concept opens doors to solving more complex problems involving infinite series and products.
Applications in Different Mathematical Contexts
The principles illustrated by this simple problem have wide-ranging applications. Here are a few examples:
- Probability: Fractions are frequently used to represent probabilities. Imagine a series of independent events, each with a certain probability of success. Multiplying the probabilities of each event gives the overall probability of all events occurring. This problem mirrors that type of calculation.
- Combinatorics: Combinatorics involves counting the number of ways to arrange or select objects. Fractions often appear in combinatorial calculations, and understanding how to manipulate fractions is crucial.
- Calculus: As mentioned earlier, telescoping products are a powerful tool in calculus, particularly when dealing with infinite series and limits. The ability to recognize and utilize these patterns is essential for solving advanced calculus problems.
- Real-world applications: Fractions are used extensively in everyday life, from measuring ingredients in cooking to calculating percentages in finance. Understanding fraction multiplication is a fundamental skill for navigating various aspects of our daily lives.
Frequently Asked Questions (FAQ)
-
Q: Can this pattern be extended to an infinite number of terms? A: Yes, theoretically. However, the limit of the sequence as the number of terms approaches infinity is 0. This is a fascinating concept in calculus, related to limits and infinite series.
-
Q: What if the numerator and denominator weren't consecutive integers? A: If the pattern of consecutive integers is broken, the simple cancellation method wouldn't directly apply. However, you could still multiply the fractions following the standard multiplication rules. Simplification might require more complex techniques depending on the numbers involved.
-
Q: Are there other similar mathematical patterns? A: Absolutely! Mathematics is filled with patterns and sequences. Exploring arithmetic and geometric progressions, Fibonacci sequences, and Pascal's triangle are other great ways to discover the elegance and predictability inherent in mathematics.
Conclusion: Beyond the Calculation
The seemingly simple calculation of 1/2 x 2/3 x 3/4 offers a gateway to a deeper understanding of fractions, sequences, and fundamental mathematical principles. By exploring the solution, we've uncovered the elegant pattern of telescoping products and its broad applications in various mathematical fields. This journey emphasizes that even seemingly basic mathematical problems can reveal powerful insights and connections to more advanced concepts, encouraging continued exploration and a deeper appreciation of the beauty of mathematics. The ability to identify and utilize these patterns enhances your mathematical problem-solving skills, making you more confident and efficient in tackling more complex challenges. Keep exploring, keep questioning, and keep discovering the wonders of mathematics!
Latest Posts
Latest Posts
-
Where Is Quito South America
Sep 12, 2025
-
Density Of Air At 20c
Sep 12, 2025
-
Whats 5 Percent Of 2000
Sep 12, 2025
-
What Is An Acute Effect
Sep 12, 2025
-
System Of Linear Equations Matrix
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 1/2 X 2/3 X 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.