X Squared Times X Squared
straightsci
Sep 14, 2025 · 5 min read
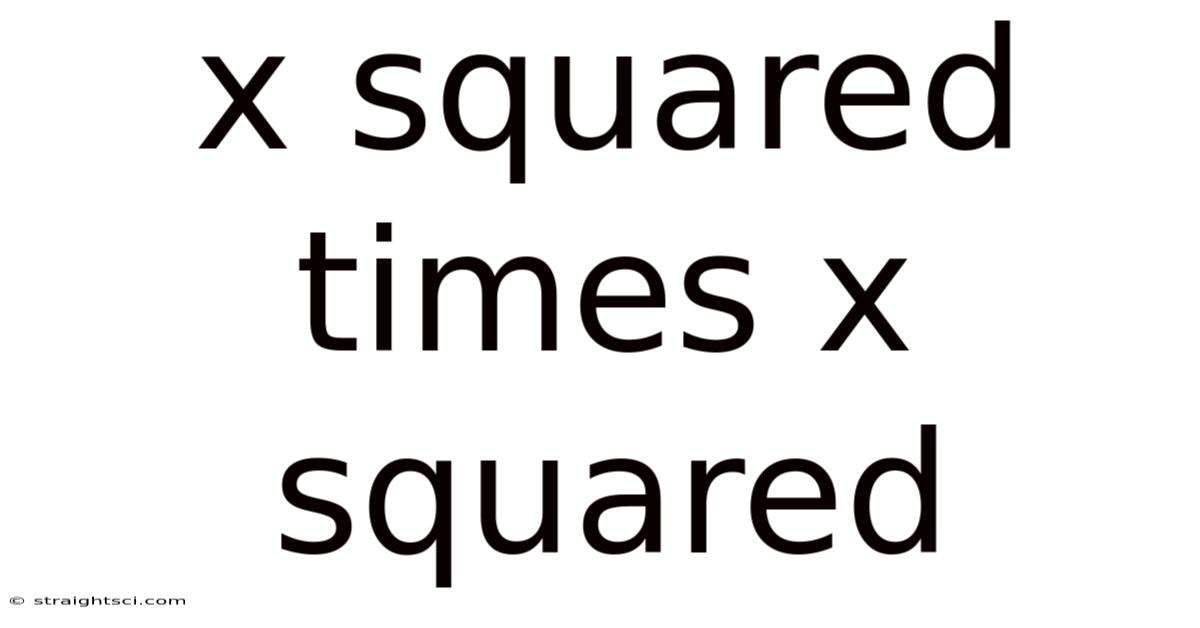
Table of Contents
Decoding x² * x²: A Deep Dive into Exponent Rules and Algebraic Simplification
Understanding how to simplify algebraic expressions like x² * x² is fundamental to mastering algebra. This seemingly simple expression holds the key to understanding crucial exponent rules and lays the groundwork for more complex mathematical operations. This article will not only explain how to solve x² * x² but will also explore the underlying principles, provide practical examples, and delve into related concepts to solidify your understanding. We'll explore the concepts in a clear, step-by-step manner, suitable for learners of all backgrounds.
Introduction: Understanding Exponents
Before tackling x² * x², let's review the basics of exponents. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. For example, in the expression x², 'x' is the base, and '2' is the exponent. This means x² is equivalent to x * x. Understanding this foundational concept is crucial for simplifying expressions involving exponents.
Simplifying x² * x²: The Rule of Multiplication with the Same Base
The core principle governing the simplification of x² * x² lies in the rule of multiplication with the same base. This rule states that when multiplying terms with the same base, you add their exponents. Mathematically, this can be represented as:
xᵃ * xᵇ = x⁽ᵃ⁺ᵇ⁾
Applying this rule to our expression, x² * x², we have:
x² * x² = x⁽²⁺²⁾ = x⁴
Therefore, x² * x² simplifies to x⁴.
Step-by-Step Breakdown: A Visual Approach
To solidify this concept, let's break down the simplification process step-by-step using a visual approach:
-
Expand the terms: Write out the expression x² * x² in its expanded form: (x * x) * (x * x).
-
Combine the terms: Notice that we have four 'x' terms being multiplied together: x * x * x * x.
-
Simplify using exponential notation: Since we are multiplying the same base ('x') four times, we can represent this concisely using exponential notation as x⁴.
This step-by-step approach emphasizes the underlying meaning of exponents and the logic behind the rule of adding exponents when multiplying terms with the same base.
Beyond the Basics: Exploring More Complex Examples
While x² * x² provides a simple illustration, the principle of adding exponents when multiplying terms with the same base applies to more complex expressions. Consider the following examples:
-
x³ * x⁵: Using the rule, x³ * x⁵ = x⁽³⁺⁵⁾ = x⁸
-
2y² * 3y⁴: Here, we multiply the coefficients (2 and 3) separately and add the exponents of the base 'y': 2 * 3 * y⁽²⁺⁴⁾ = 6y⁶
-
(a²b³) * (a⁴b): We apply the rule to each base individually: a⁽²⁺⁴⁾ * b⁽³⁺¹⁾ = a⁶b⁴
These examples demonstrate the versatility and importance of this fundamental rule in simplifying more intricate algebraic expressions. It's essential to remember that this rule only applies when the bases are the same. If the bases are different, the expression cannot be simplified further using this specific exponent rule.
The Power of a Power Rule: A Related Concept
A closely related concept is the "power of a power" rule. This rule dictates that when raising a power to another power, you multiply the exponents. The general form is:
(xᵃ)ᵇ = x⁽ᵃ*ᵇ⁾
For example:
(x²)³ = x⁽²*³⁾ = x⁶
This rule is frequently used in conjunction with the rule for multiplying terms with the same base. Consider this example:
(x²)³ * x⁴ = x⁶ * x⁴ = x¹⁰
Addressing Common Mistakes and Misconceptions
Several common mistakes can hinder a clear understanding of exponent rules. Let's address some of these:
-
Incorrectly multiplying exponents when multiplying terms: Remember, you add exponents when multiplying terms with the same base, not multiply them. This is a frequent error.
-
Forgetting to apply the rule to all bases: When simplifying expressions with multiple bases, ensure that you apply the addition of exponents rule to each base separately.
-
Confusing the power of a power rule with multiplying terms: The power of a power rule involves multiplying exponents, while multiplying terms with the same base involves adding exponents. These are distinct operations.
Practice is key to avoiding these common errors and mastering the application of exponent rules.
Frequently Asked Questions (FAQ)
Q: What happens if the exponents are negative?
A: The same rules apply to negative exponents. Remember that x⁻ⁿ = 1/xⁿ. For instance, x⁻² * x³ = x⁽⁻²⁺³⁾ = x¹.
Q: Can I simplify x² + x²?
A: No. This is a different operation. You can simplify this expression by combining like terms: x² + x² = 2x². This involves addition, not multiplication.
Q: What if the bases are different?
A: If the bases are different, you cannot simplify the expression by adding exponents. For example, x² * y² cannot be simplified further.
Q: How do I handle expressions with coefficients?
A: Multiply the coefficients separately and then apply the exponent rules to the variables with the same base. For example, 3x² * 2x³ = (3 * 2) * x⁽²⁺³⁾ = 6x⁵.
Q: Why is understanding exponent rules important?
A: Exponent rules are fundamental in algebra and beyond. They are crucial for simplifying expressions, solving equations, and working with polynomials, functions, and more advanced mathematical concepts. A strong grasp of these rules is essential for success in higher-level mathematics and science.
Conclusion: Mastering the Fundamentals of Algebraic Simplification
Mastering the simplification of expressions like x² * x² is crucial for building a strong foundation in algebra. By understanding the fundamental rule of adding exponents when multiplying terms with the same base, and by practicing with various examples, you can confidently tackle more complex algebraic expressions. Remember to carefully review the steps, avoid common mistakes, and continuously practice to solidify your understanding of this fundamental concept. The ability to efficiently simplify algebraic expressions is a critical skill that will serve you well throughout your mathematical journey. With consistent effort and a clear understanding of the underlying principles, you can confidently navigate the world of exponents and unlock the power of algebraic simplification.
Latest Posts
Latest Posts
-
How To Rationalize A Denominator
Sep 14, 2025
-
Where Does Calvin Cycle Occur
Sep 14, 2025
-
Ultraviolet Light For Bed Bugs
Sep 14, 2025
-
Convert 190 C To F
Sep 14, 2025
-
10 Tbsp Butter In Grams
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about X Squared Times X Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.