X 3 X 4 8
straightsci
Sep 09, 2025 · 6 min read
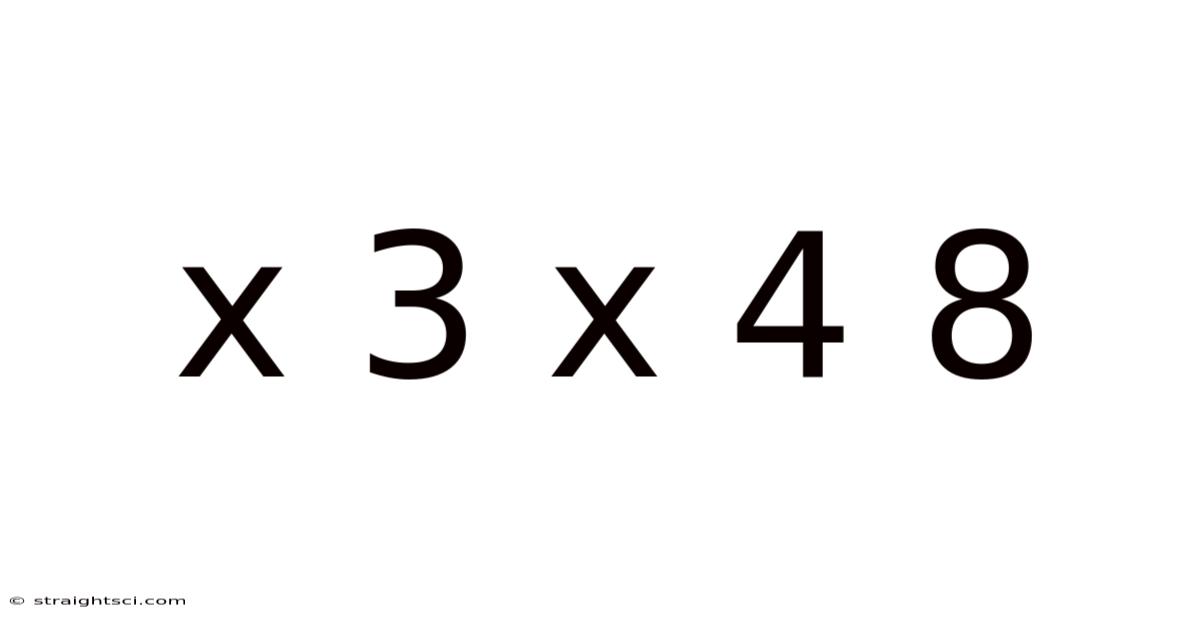
Table of Contents
Unlocking the Mystery: Exploring the Mathematical Expression "x 3 x 4 = 8"
This seemingly simple equation, "x 3 x 4 = 8," initially presents itself as a straightforward arithmetic problem. However, a deeper dive reveals a fascinating exploration into the world of algebra, problem-solving strategies, and the importance of understanding mathematical notation. This article will dissect the equation, offering multiple approaches to solving it, exploring its underlying mathematical principles, and addressing common misconceptions. We'll also delve into how this simple expression can serve as a stepping stone to more complex algebraic concepts.
Understanding the Problem: What Does "x 3 x 4 = 8" Mean?
At first glance, the equation might appear incomplete or even erroneous. Standard arithmetic would suggest multiplying x by 3, then multiplying the result by 4, leading to a final answer of 12x. However, the inclusion of the result "8" implies that this is not a standard multiplication problem. The key lies in recognizing the need for a different approach, one that moves beyond basic arithmetic into the realm of algebraic thinking. This requires us to consider the potential for different interpretations of the symbols and operations involved.
Approach 1: Interpreting the Equation as a Single Expression
One approach involves treating the expression "x 3 x 4" as a single, compact algebraic representation. We can rewrite this expression more clearly as (x * 3) * 4 = 8. By following the order of operations (PEMDAS/BODMAS), we first multiply x by 3, and then multiply the result by 4. This gives us 12x = 8. To solve for x, we divide both sides of the equation by 12:
x = 8/12 = 2/3
Therefore, using this interpretation, the solution to the equation is x = 2/3.
Approach 2: Considering Alternative Interpretations
The ambiguity of the original equation allows for alternative interpretations. The spaces between the elements could suggest a different arrangement of operations. For example, it's possible the expression is meant to be:
x * (3 * 4) = 8
Following the order of operations, we first calculate 3 * 4 = 12. The equation then becomes:
12x = 8
Dividing both sides by 12, we again arrive at:
x = 8/12 = 2/3
This interpretation reinforces the solution obtained in Approach 1. It highlights the importance of precise mathematical notation and the potential for misinterpretations arising from ambiguous spacing.
Approach 3: Exploring the Concept of Implicit Multiplication
Another layer of complexity can be added by considering the concept of implicit multiplication. In some mathematical contexts, particularly in programming or certain algebraic notations, the juxtaposition of variables or numbers can imply multiplication without an explicit multiplication symbol. This could lead to a different interpretation of the equation.
If we interpret the expression as x3 x 4 (where x3 implies x multiplied by 3), the equation becomes:
(3x) * 4 = 8
Simplifying this leads to:
12x = 8
And the solution remains:
x = 8/12 = 2/3
The Significance of Order of Operations (PEMDAS/BODMAS)
The order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), plays a crucial role in solving mathematical equations. This consistent sequence ensures that the solution is unambiguous and universally applicable. In all the approaches discussed above, adhering to the order of operations was critical to arriving at the correct answer. Incorrect application of the order of operations would lead to an incorrect solution.
Addressing Potential Misconceptions
A common misconception stems from the intuitive assumption that the equation should be solvable using only basic arithmetic. However, the presence of the unknown variable 'x' necessitates the application of algebraic techniques. Another misconception might arise from interpreting the equation's structure as a simple sequence of multiplications without considering the underlying algebraic meaning.
Extending the Concept: Moving Beyond Simple Equations
This seemingly simple equation serves as a valuable foundation for understanding more complex algebraic concepts. Solving for 'x' in this equation introduces students to the fundamentals of solving algebraic equations, including:
- Isolating the variable: The process of manipulating the equation to isolate 'x' on one side is a cornerstone of algebra.
- Inverse operations: To solve for x, we used the inverse operation of multiplication (division). Understanding inverse operations is crucial for solving a wide range of equations.
- Fractional solutions: The solution x = 2/3 highlights that algebraic solutions aren't always whole numbers. This prepares students for dealing with fractional and decimal solutions in more advanced algebraic problems.
Furthermore, the problem encourages critical thinking about the interpretation of mathematical notation and the potential ambiguities that can arise from unclear or imprecise expression.
The Importance of Precise Mathematical Notation
This exercise emphasizes the importance of clear and unambiguous mathematical notation. The ambiguity in the original expression highlights the need for precise writing to avoid misinterpretations. Using parentheses or explicitly writing multiplication symbols eliminates potential confusion and ensures accurate problem-solving.
Frequently Asked Questions (FAQ)
-
Q: Is there only one correct answer to this equation?
- A: Based on the most likely interpretations of the given notation, yes, the solution is consistently x = 2/3. However, without clearer notation, other interpretations are possible, leading to different outcomes.
-
Q: Why is it important to follow the order of operations?
- A: Following the order of operations ensures a consistent and universally accepted method for solving mathematical expressions. Ignoring the order of operations can lead to incorrect results.
-
Q: Can this equation be solved graphically?
- A: While not a standard approach for such a simple equation, it could be represented graphically by plotting the function y = 12x and finding the point where y = 8. The x-coordinate of that point would be the solution.
-
Q: What are some real-world applications of solving equations like this?
- A: Solving equations forms the basis for countless applications in science, engineering, finance, and everyday life. From calculating distances and speeds to modeling financial growth, the principles are widespread.
Conclusion: The Power of Simple Equations
The equation "x 3 x 4 = 8" might initially seem trivial, but a careful analysis reveals a rich tapestry of mathematical concepts. It serves as a microcosm of algebraic problem-solving, highlighting the significance of precise notation, the application of the order of operations, and the importance of critical thinking in interpreting mathematical expressions. By understanding the different approaches to solving this equation, we gain a deeper appreciation for the power and elegance of algebra, and its fundamental role in various aspects of science, engineering, and everyday life. The seemingly simple act of solving for 'x' opens doors to a wider understanding of mathematical reasoning and problem-solving skills that extend far beyond this initial problem. The journey from simple arithmetic to the application of algebraic techniques is a testament to the gradual development of mathematical understanding and problem-solving skills.
Latest Posts
Latest Posts
-
How To Remove Drawer Slides
Sep 10, 2025
-
I Miss You In Germany
Sep 10, 2025
-
Math Questions For 12th Graders
Sep 10, 2025
-
Internal Temperature Of Ground Pork
Sep 10, 2025
-
What Is The Ribosomes Function
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about X 3 X 4 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.