X 2 Y 2 1
straightsci
Sep 16, 2025 · 7 min read
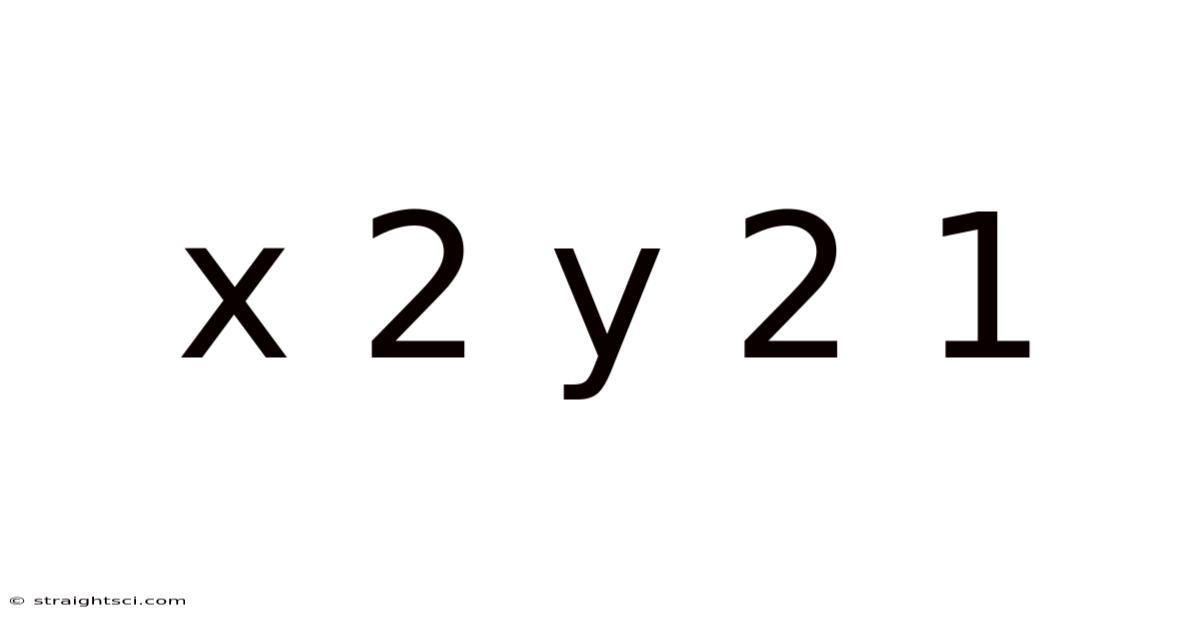
Table of Contents
Decoding the Equation: x² + y² = 1 – A Deep Dive into the Unit Circle
The deceptively simple equation, x² + y² = 1, might seem insignificant at first glance. However, this seemingly basic algebraic expression unlocks a world of mathematical concepts, forming the foundation for trigonometry, complex numbers, and even aspects of physics and engineering. This article will delve deep into the meaning and implications of x² + y² = 1, exploring its geometric representation, its connection to trigonometric functions, and its broader significance in mathematics. We'll uncover why understanding this equation is crucial for anyone pursuing a deeper understanding of mathematics and its applications.
Introduction: The Geometric Beauty of the Unit Circle
The equation x² + y² = 1 defines a unit circle – a circle with a radius of 1 centered at the origin (0,0) of a Cartesian coordinate system. This seemingly simple shape holds immense mathematical significance. Every point (x, y) that satisfies this equation lies precisely on the circumference of the unit circle. This geometric interpretation is crucial to understanding the equation's power. The equation itself is derived directly from the Pythagorean theorem, a fundamental concept in geometry. Remember that the Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides. In the unit circle, the hypotenuse is the radius (which is 1), and the other two sides are represented by x and y.
Understanding the Equation Through Points on the Circle
Let's consider some specific points on the unit circle to solidify our understanding.
- (1, 0): This point represents the intersection of the unit circle with the positive x-axis. Plugging these values into the equation, we get 1² + 0² = 1, which is true.
- (0, 1): This point represents the intersection with the positive y-axis. Again, the equation holds true: 0² + 1² = 1.
- (-1, 0): The intersection with the negative x-axis. (-1)² + 0² = 1.
- (0, -1): The intersection with the negative y-axis. 0² + (-1)² = 1.
- (√2/2, √2/2): This point lies in the first quadrant, at a 45-degree angle from the positive x-axis. Let's verify: (√2/2)² + (√2/2)² = (2/4) + (2/4) = 1.
These examples demonstrate how any point (x, y) satisfying x² + y² = 1 lies exactly on the circumference of the unit circle. The equation itself acts as a constraint, defining the set of all possible points that form the circle.
The Unit Circle and Trigonometric Functions: A Fundamental Connection
The unit circle is inextricably linked to trigonometric functions such as sine, cosine, and tangent. For any point (x, y) on the unit circle, the coordinates are directly related to these functions:
- x = cos(θ): The x-coordinate is equal to the cosine of the angle θ formed between the positive x-axis and the line connecting the origin to the point (x, y).
- y = sin(θ): The y-coordinate is equal to the sine of the same angle θ.
- tan(θ) = y/x: The tangent of θ is the ratio of the y-coordinate to the x-coordinate.
This relationship is fundamental to trigonometry. The unit circle provides a visual and intuitive way to understand the behavior of trigonometric functions for all angles, not just those within the typical 0° to 90° range. It allows us to visualize the periodic nature of these functions, showing how their values repeat every 360° (or 2π radians).
Extending the Understanding: Polar Coordinates and Parametric Equations
While the Cartesian coordinates (x, y) are useful, representing points on the unit circle using polar coordinates (r, θ) offers a more natural and intuitive approach. In polar coordinates, 'r' represents the distance from the origin, and 'θ' represents the angle from the positive x-axis. Since the unit circle has a radius of 1, the equation in polar coordinates simplifies to:
- r = 1
This means that regardless of the angle θ, the distance from the origin always remains 1, precisely defining the unit circle.
We can also represent the unit circle using parametric equations, expressing x and y in terms of a parameter, typically the angle θ:
- x = cos(θ)
- y = sin(θ)
These equations provide a dynamic way to trace the points on the unit circle as θ varies.
Applications Beyond Geometry: The Unit Circle in Complex Numbers
The equation x² + y² = 1 extends its reach beyond geometry. It plays a crucial role in the realm of complex numbers. A complex number is represented as z = x + iy, where 'i' is the imaginary unit (√-1). The equation x² + y² = 1 can be rewritten as:
- |z|² = 1
where |z| represents the magnitude or modulus of the complex number z. This means that the equation represents the set of all complex numbers with a magnitude of 1. These numbers are known as complex numbers on the unit circle, and they have unique properties and applications in various areas of mathematics and physics.
Applications in Physics and Engineering: Rotational Motion and Oscillations
The unit circle isn't just a mathematical curiosity; it has practical applications in various fields. In physics and engineering, the unit circle is fundamental to understanding:
- Rotational motion: The circular motion of objects can be modeled using trigonometric functions derived from the unit circle. Analyzing angular velocity, acceleration, and displacement relies heavily on this concept.
- Oscillations: Simple harmonic motion (like a pendulum or a spring) can be described using sinusoidal functions (sine and cosine), which are directly related to the unit circle. Understanding the unit circle aids in analyzing these oscillations.
- Signal processing: In electrical engineering, signals are often represented as complex numbers. The unit circle is crucial in analyzing and manipulating these signals in the frequency domain using techniques like Fourier transforms.
Frequently Asked Questions (FAQ)
-
What is the significance of the "1" in the equation x² + y² = 1? The "1" represents the radius of the circle. If it were a different number, say "4", the equation x² + y² = 4 would represent a circle with a radius of 2.
-
Can the equation x² + y² = 1 be used to represent other shapes? No, this specific equation only represents a circle with a radius of 1 centered at the origin. Other equations are needed to represent different shapes.
-
How does the unit circle relate to radians? Angles in the unit circle are often measured in radians, where one radian is the angle subtended at the center of the circle by an arc of length equal to the radius. This is a natural unit for measuring angles in the context of the unit circle.
-
Why is the unit circle so important in trigonometry? The unit circle provides a geometric interpretation of trigonometric functions, allowing us to visualize their values and periodic behavior for all angles. It simplifies the understanding and application of trigonometric identities and relationships.
-
Are there any real-world examples of the unit circle? The principles of the unit circle are applied in numerous real-world applications, including rotational mechanics, electrical circuits, and signal processing. While you won't see a physical unit circle in most cases, its underlying principles are fundamental to many technologies and phenomena.
Conclusion: The Enduring Power of a Simple Equation
The seemingly simple equation x² + y² = 1, representing the unit circle, has far-reaching implications across multiple branches of mathematics, and extends into practical applications in physics and engineering. Its geometric interpretation, its relationship to trigonometric functions, and its significance in complex numbers demonstrate its fundamental role in mathematical understanding. Mastering this equation unlocks a deeper appreciation for the interconnectedness of various mathematical concepts and provides a powerful foundation for further mathematical exploration. From understanding simple harmonic motion to analyzing complex signals, the unit circle serves as a cornerstone of mathematical understanding and application. Its seemingly simple form belies its profound and enduring power.
Latest Posts
Latest Posts
-
5 Signs Of Chemical Change
Sep 16, 2025
-
How To Find Missing Angles
Sep 16, 2025
-
Periodic Table By Electron Configuration
Sep 16, 2025
-
Fastest Words Per Minute Typed
Sep 16, 2025
-
How To Calculate Class Width
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about X 2 Y 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.