X 2 X 3 12
straightsci
Sep 20, 2025 · 7 min read
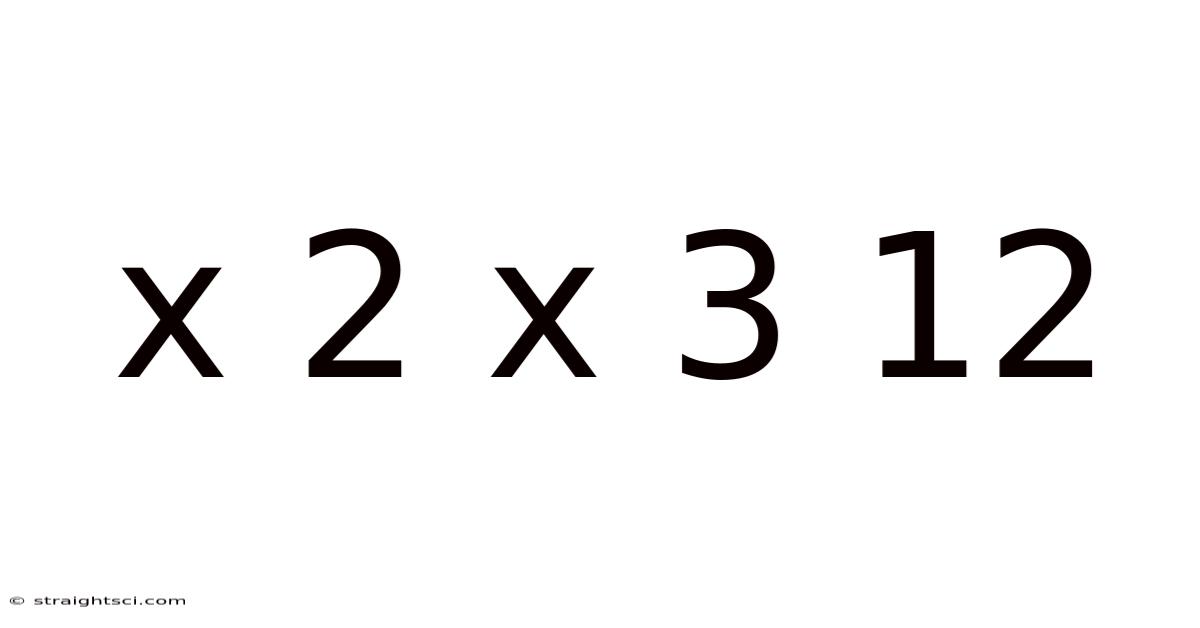
Table of Contents
Unlocking the Mystery of 2 x 3 x 12: A Deep Dive into Multiplication and its Applications
The simple equation "2 x 3 x 12 = 72" might seem trivial at first glance. However, this seemingly straightforward calculation opens a door to a vast world of mathematical concepts, practical applications, and even philosophical considerations about the nature of numbers and their relationships. This article will delve deep into the meaning and implications of this equation, exploring its fundamental components, exploring related mathematical principles, and showcasing its relevance in various real-world scenarios. We’ll go beyond the simple answer and uncover the rich tapestry woven within this seemingly basic multiplication problem.
Understanding the Fundamentals: Multiplication as Repeated Addition
Before we dive into the intricacies of 2 x 3 x 12, let's refresh our understanding of multiplication itself. At its core, multiplication is simply a concise way of expressing repeated addition. For instance, 2 x 3 means adding the number 2 three times: 2 + 2 + 2 = 6. This fundamental concept forms the bedrock upon which more complex mathematical operations are built.
In our equation, 2 x 3 x 12, we can break it down step-by-step. First, we can tackle 2 x 3, which equals 6. Then, we multiply this result by 12: 6 x 12 = 72. This demonstrates the associative property of multiplication, meaning we can group the numbers in different ways without affecting the final result. (2 x 3) x 12 = 2 x (3 x 12) = 72.
The Commutative Property and its Implications
Another crucial property of multiplication is the commutative property. This means that the order of the numbers doesn't change the product. Therefore, 2 x 3 x 12 is the same as 3 x 2 x 12, 12 x 3 x 2, and so on. Understanding this property allows for flexibility in calculations and problem-solving. This seemingly simple observation has significant consequences when dealing with larger, more complex equations.
For instance, consider the scenario of arranging chairs in a room. If you have 2 rows of 3 chairs, then 12 similar sets of chairs, you can easily visualize the total number of chairs using this commutative property. Whether you calculate 2 x 3 first, then multiply by 12, or any other order, you’ll always arrive at the same answer: 72 chairs.
Beyond the Basics: Exploring Factors and Multiples
The numbers in our equation – 2, 3, and 12 – are interconnected through the concepts of factors and multiples. Factors are numbers that divide evenly into another number without leaving a remainder. For example, 2, 3, 4, and 6 are all factors of 12. Multiples, on the other hand, are the results of multiplying a number by integers. Thus, 12 is a multiple of 2, 3, 4, and 6.
Understanding factors and multiples is essential in various mathematical applications, including prime factorization, greatest common divisor (GCD) calculations, and least common multiple (LCM) computations. These concepts are fundamental for simplifying fractions, solving algebraic equations, and working with more complex mathematical structures.
Prime Factorization and its Significance
The concept of prime factorization plays a significant role in comprehending the relationship between the numbers in our equation. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11). Prime factorization involves expressing a number as a product of its prime factors.
The prime factorization of 12 is 2 x 2 x 3 (or 2² x 3). Notice how the numbers 2 and 3, already present in our original equation (2 x 3 x 12), are fundamental components of 12's prime factorization. This illustrates the interconnectedness of numbers and how the prime factorization reveals the underlying structure of seemingly disparate values. Prime factorization is an essential tool in cryptography, number theory, and various other advanced mathematical fields.
Real-World Applications: From Baking to Building
The seemingly simple equation 2 x 3 x 12 has numerous practical applications in everyday life. Consider these examples:
- Baking: If you need to bake 12 cookies and each batch requires 2 x 3 = 6 cookies, then you’ll need to bake 2 batches (12 / 6 = 2). This showcases the direct application of division, which is the inverse operation of multiplication.
- Construction: If you’re building a wall and each section requires 12 bricks, and you need 2 sections in three separate parts of the building, then you need 72 bricks (2 x 3 x 12 = 72). This highlights the importance of accurate calculations in practical scenarios where resources are limited.
- Inventory Management: If a store sells boxes containing 12 items each, and they have 2 stacks with 3 boxes per stack, it’s easy to determine the total number of items: 72 items (2 x 3 x 12 = 72). This demonstrates how multiplication helps in efficiently managing stock levels.
- Financial Calculations: In simple compound interest calculations, we often deal with multiplications of factors representing interest rates, time periods and principal amounts. Although often more complex than our simple equation, the fundamental principle remains the same.
Extending the Concept: Geometry and Volume
The equation 2 x 3 x 12 can also be visualized geometrically. Imagine a rectangular prism (a box) with dimensions of 2 units, 3 units, and 12 units. The product 2 x 3 x 12 represents the volume of this prism, calculated by multiplying its length, width, and height. This highlights the connection between arithmetic operations and geometric concepts. This visualization can be incredibly helpful in understanding three-dimensional space and its applications in various fields like architecture, engineering, and design.
Moving Beyond the Numbers: A Philosophical Perspective
The equation 2 x 3 x 12, while seemingly simple, invites a deeper philosophical contemplation. It demonstrates the inherent order and structure within the numerical system. The fact that these seemingly arbitrary numbers combine to produce a specific, predictable result speaks to the underlying laws governing mathematics. This predictability and consistency are fundamental to our understanding of the universe and our ability to make accurate predictions and build models. The simple elegance of this equation underscores the profound beauty and power of mathematical principles.
Frequently Asked Questions (FAQ)
-
Q: What is the most efficient way to calculate 2 x 3 x 12?
- A: While the order doesn't matter due to the commutative and associative properties, many find calculating 2 x 3 = 6 first, then 6 x 12 = 72, to be the most straightforward method.
-
Q: Are there other ways to represent the number 72?
- A: Yes, infinitely many. 72 can be expressed as a sum of numbers, a difference between numbers, and through various other mathematical operations. For example, 72 = 36 + 36 or 72 = 100 - 28. Its prime factorization (2³ x 3²) is a unique representation.
-
Q: How does this equation relate to more advanced mathematical concepts?
- A: This simple equation serves as a foundation for understanding more complex concepts like algebraic equations, calculus, linear algebra, and abstract algebra. The principles of commutativity, associativity, and factorization are fundamental across many mathematical disciplines.
-
Q: Can this equation be used to solve real-world problems that are more complex than the examples provided?
- A: Yes, absolutely. While the examples provided were simple, the underlying principle of multiplication is used in numerous complex applications across engineering, finance, physics, computer science, and many other fields. The equation serves as a fundamental building block for more complex calculations.
Conclusion: The Enduring Power of a Simple Equation
The equation 2 x 3 x 12 = 72, while seemingly insignificant, serves as a powerful microcosm of mathematics. From its foundational role in understanding multiplication and its properties to its far-reaching applications in various fields, this simple equation underscores the profound impact of even the most basic mathematical principles. By exploring its intricacies, we gain a deeper appreciation for the elegance, power, and universality of mathematics, highlighting its role in understanding our world and shaping our future. This seemingly simple calculation unlocks a wealth of knowledge, proving that even the smallest elements can hold immense significance. The journey from a simple equation to a profound understanding of mathematical principles highlights the beauty and power of continuous learning and exploration.
Latest Posts
Latest Posts
-
Does Great Britain Celebrate Thanksgiving
Sep 20, 2025
-
1 73 Meters In Feet
Sep 20, 2025
-
How To Find The Gcf
Sep 20, 2025
-
Chemical Formula For Sodium Sulphate
Sep 20, 2025
-
Literary Devices Vs Literary Techniques
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about X 2 X 3 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.