What's Half Of 3 4
straightsci
Sep 19, 2025 · 5 min read
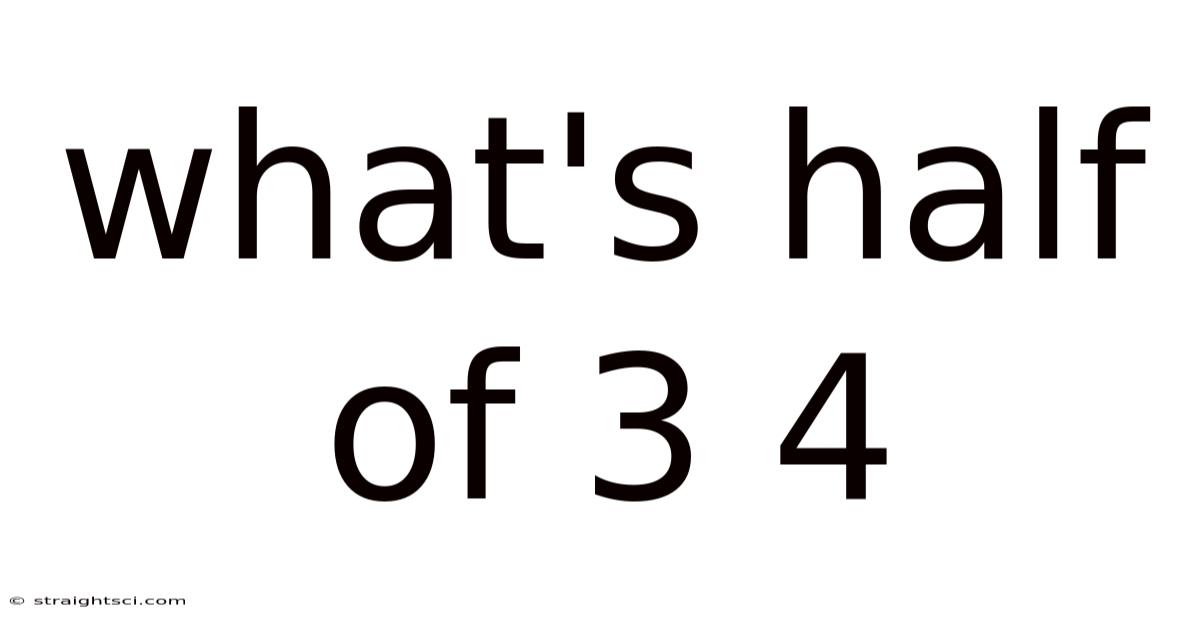
Table of Contents
What's Half of 3/4? A Deep Dive into Fractions and Their Applications
Finding half of 3/4 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding this seemingly basic calculation unlocks a deeper appreciation of fractions, their manipulation, and their widespread applications in various fields. This article will not only answer the question "What's half of 3/4?" but will also explore the underlying mathematical principles, provide multiple solution methods, and delve into real-world examples showcasing the relevance of fractional calculations.
Understanding Fractions: A Quick Recap
Before diving into the problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It is expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator, meaning we have 3 out of 4 equal parts.
Method 1: Dividing the Numerator
The most straightforward method to find half of 3/4 is to divide the numerator by 2. Since we're finding half, we're essentially dividing the fraction by 2. Remember that dividing a fraction by a whole number is the same as multiplying the fraction by the reciprocal of the whole number. The reciprocal of 2 is 1/2. Therefore:
(3/4) / 2 = (3/4) * (1/2) = 3/8
Therefore, half of 3/4 is 3/8.
Method 2: Dividing the Whole
Alternatively, we can visualize the problem. Imagine a pizza cut into 4 equal slices. 3/4 of the pizza represents 3 slices. To find half of 3/4, we need to find half of those 3 slices. Dividing 3 slices in half gives us 1.5 slices. However, we need to express this in terms of the original fourths. Since each slice represents 1/4 of the pizza, 1.5 slices represent 1.5 * (1/4) = 3/8 of the pizza.
This method provides a more intuitive understanding of the process, particularly helpful for visual learners.
Method 3: Using Decimal Representation
We can also solve this problem using decimal representation. First, convert the fraction 3/4 into a decimal by dividing the numerator by the denominator:
3 ÷ 4 = 0.75
Then, find half of 0.75:
0.75 ÷ 2 = 0.375
Finally, convert the decimal back into a fraction. 0.375 can be written as 375/1000. Simplifying this fraction by dividing both the numerator and the denominator by their greatest common divisor (125) gives us:
375/1000 = 3/8
This method demonstrates the interchangeability between fractions and decimals and reinforces the equivalence of different representations of the same value.
Real-World Applications of Fractional Calculations
Fractional calculations, seemingly simple, are fundamental to numerous real-world scenarios. Here are a few examples:
-
Cooking and Baking: Recipes often call for fractional amounts of ingredients. For instance, a recipe might require 3/4 cup of flour, and you might want to halve the recipe. Understanding how to find half of 3/4 is crucial for accurate measurements.
-
Construction and Engineering: Precise measurements are essential in construction and engineering. Calculations involving fractions are used to determine the dimensions of components, ensuring accurate fitting and functionality.
-
Finance: Fractions are extensively used in financial calculations, such as calculating interest rates, determining proportions of investments, and understanding stock market fluctuations. For example, understanding fractional shares allows investors to buy smaller portions of a company's stock.
-
Science: Fractions are ubiquitous in scientific measurements and calculations. Scientific notation often involves fractional exponents, and many formulas in physics and chemistry incorporate fractions. For example, in chemistry, concentrations of solutions are often expressed as fractions or percentages, which are simply fractions with a denominator of 100.
Expanding the Concept: Beyond Halving
The process of finding half of 3/4 can be extended to finding other fractions of 3/4. For example, to find one-third of 3/4, we would multiply 3/4 by 1/3:
(3/4) * (1/3) = 1/4
Similarly, to find two-thirds of 3/4, we would multiply 3/4 by 2/3:
(3/4) * (2/3) = 6/12 = 1/2
These calculations highlight the versatility of fractions and the ease with which they can be manipulated to solve various problems.
Frequently Asked Questions (FAQs)
Q: Can I solve this problem by converting 3/4 to a percentage first?
A: Yes, absolutely! Converting 3/4 to a percentage gives us 75%. Half of 75% is 37.5%, which, when converted back to a fraction, is 37.5/100 = 3/8. This method is equally valid.
Q: What if the numerator wasn't divisible by 2?
A: If the numerator wasn't divisible by 2, the resulting fraction would simply be an improper fraction. For example, if we wanted to find half of 5/8, the calculation would be: (5/8) * (1/2) = 5/16. Improper fractions are perfectly acceptable and often represent values greater than 1.
Q: Are there other ways to simplify fractions?
A: Yes, the greatest common divisor (GCD) method is often used to simplify fractions. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. Dividing both the numerator and the denominator by their GCD results in the simplest form of the fraction. For example, in simplifying 6/12, the GCD is 6, so we divide both the numerator and the denominator by 6, resulting in 1/2.
Q: Why is understanding fractions important?
A: Understanding fractions is crucial for various aspects of life, from daily tasks to complex scientific calculations. It builds a strong foundation in mathematics and improves problem-solving skills.
Conclusion
Finding half of 3/4, while seemingly straightforward, provides a valuable opportunity to revisit and reinforce fundamental concepts related to fractions. The multiple solution methods presented highlight the flexibility and adaptability of fractional arithmetic. Moreover, understanding fractional calculations extends far beyond the classroom, finding practical applications in various professions and everyday scenarios. This deep dive into the seemingly simple problem of halving 3/4 demonstrates its broader significance and emphasizes the importance of mastering fractional arithmetic for success in diverse fields. Remember, the seemingly simple often holds a wealth of underlying complexity and practical applications waiting to be discovered.
Latest Posts
Latest Posts
-
22 Pounds How Many Kg
Sep 19, 2025
-
Latitude And Longitude Of Beijing
Sep 19, 2025
-
When Did Usa Join Ww2
Sep 19, 2025
-
Function Of Rectus Abdominis Muscle
Sep 19, 2025
-
How To Determine Percent Recovery
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What's Half Of 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.