Whats A Half Of 1/3
straightsci
Sep 18, 2025 · 5 min read
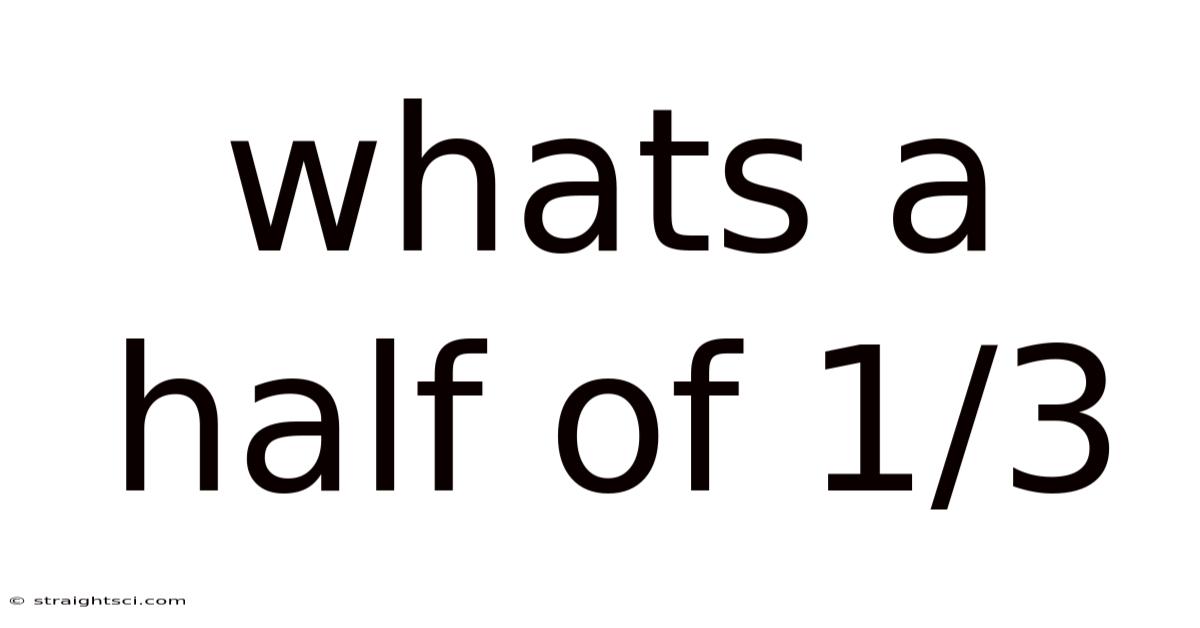
Table of Contents
What's Half of 1/3? Understanding Fractions and Division
Finding half of one-third might seem like a simple task, but it's a fundamental concept in mathematics that underlies a wide range of applications. This article will explore what half of 1/3 is, explain the process of solving this type of problem, delve into the underlying mathematical principles, and address common misconceptions. Understanding fractions and division is crucial not only for academic success but also for everyday problem-solving in various fields.
Introduction: The Basics of Fractions
Before diving into the specifics of finding half of 1/3, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts we are considering. For example, in the fraction 1/3, the denominator (3) signifies that the whole is divided into three equal parts, and the numerator (1) signifies that we are considering only one of those parts.
Calculating Half of 1/3: A Step-by-Step Approach
Finding half of 1/3 involves dividing the fraction 1/3 by 2. There are several ways to approach this calculation:
Method 1: Direct Division
We can write this as a division problem: (1/3) ÷ 2. To divide a fraction by a whole number, we multiply the fraction by the reciprocal of the whole number. The reciprocal of 2 is 1/2. So, the problem becomes:
(1/3) x (1/2) = 1/6
Therefore, half of 1/3 is 1/6.
Method 2: Visual Representation
Imagine a circle or a rectangular bar divided into three equal parts. Shading one part represents 1/3. Now, to find half of that shaded area, divide the shaded area into two equal parts. You will find that each of these smaller parts represents 1/6 of the original whole. This visual method helps to build an intuitive understanding of the concept.
Method 3: Using Decimals (For Approximation)
While fractions are often preferred for accuracy, converting to decimals can provide an approximate understanding.
1/3 ≈ 0.333...
Half of 0.333... ≈ 0.1666...
This decimal, 0.1666..., is approximately equal to 1/6. Keep in mind that this is an approximation due to the repeating decimal nature of 1/3. Fractions provide exactness in this context.
The Mathematical Principles Involved
The process of finding half of 1/3 relies on fundamental principles of fraction arithmetic:
-
Multiplication of Fractions: To multiply fractions, we multiply the numerators together and the denominators together. This is precisely what we did in Method 1: (1/3) x (1/2) = (1 x 1) / (3 x 2) = 1/6.
-
Reciprocal: The reciprocal of a number is 1 divided by that number. In division of fractions, we use the reciprocal of the divisor (the number we are dividing by). Dividing by 2 is the same as multiplying by its reciprocal, 1/2.
-
Equivalent Fractions: It's important to remember that fractions can have multiple equivalent forms. For instance, 1/6, 2/12, 3/18, and so on, are all equivalent fractions representing the same value.
Expanding the Concept: Beyond Halves
The same principles apply when finding other fractions of 1/3 or any other fraction. For example, to find one-quarter (1/4) of 1/3, we would perform the following calculation:
(1/3) x (1/4) = 1/12
Similarly, finding two-thirds (2/3) of 1/3 involves:
(1/3) x (2/3) = 2/9
Real-World Applications
Understanding fractions and the process of calculating fractions of fractions is crucial in various real-world scenarios. Here are just a few examples:
-
Cooking and Baking: Recipes often require fractions of ingredients. For example, a recipe might call for 1/3 cup of sugar, and you might need to halve that amount.
-
Construction and Engineering: Precise measurements are vital in these fields, often involving fractions of inches or centimeters.
-
Finance: Calculating percentages, interest rates, and proportions of investments frequently involves fraction arithmetic.
-
Data Analysis: Analyzing data and representing proportions often involves the use of fractions and percentages.
Frequently Asked Questions (FAQ)
Q: Why can't I simply divide 1 by 3 and then divide the result by 2?
A: While you can do this with a calculator to get an approximate decimal answer, working directly with fractions maintains accuracy. Decimal representations of fractions, especially those with repeating decimals like 1/3, can introduce rounding errors.
Q: Is there a different way to solve this problem?
A: The methods outlined above (direct division, visual representation, and using decimals for approximation) are the most common and straightforward approaches. However, the underlying principles of fraction arithmetic remain the same regardless of the chosen method.
Q: What if I need to find a fraction of a fraction that has a larger numerator than denominator (an improper fraction)?
A: The same principles still apply. Remember to multiply the numerators and denominators separately. You might need to simplify the resulting fraction to its lowest terms.
Q: How can I improve my understanding of fractions?
A: Practice is key! Try solving various fraction problems, both simple and complex. Visual aids like diagrams can also help build intuition. Consider reviewing the fundamentals of fraction addition, subtraction, multiplication, and division.
Conclusion: Mastering Fractions
Finding half of 1/3, resulting in 1/6, might seem like a simple calculation, but it highlights the crucial importance of understanding fractions and their arithmetic. By mastering these concepts, you'll not only improve your mathematical skills but also gain a valuable tool applicable across diverse fields and everyday life situations. Remember to practice regularly and to explore different approaches to deepen your comprehension and build confidence in tackling fraction-related problems. The ability to work confidently with fractions is a fundamental building block for further mathematical exploration and problem-solving abilities.
Latest Posts
Latest Posts
-
What Does Ghs Stand For
Sep 18, 2025
-
Definition Of A Social Issue
Sep 18, 2025
-
Total World War 2 Casualties
Sep 18, 2025
-
Mr Brunner The Lightning Thief
Sep 18, 2025
-
New York Distance From Boston
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Whats A Half Of 1/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.