Whats 30 Percent Of 200
straightsci
Sep 23, 2025 · 5 min read
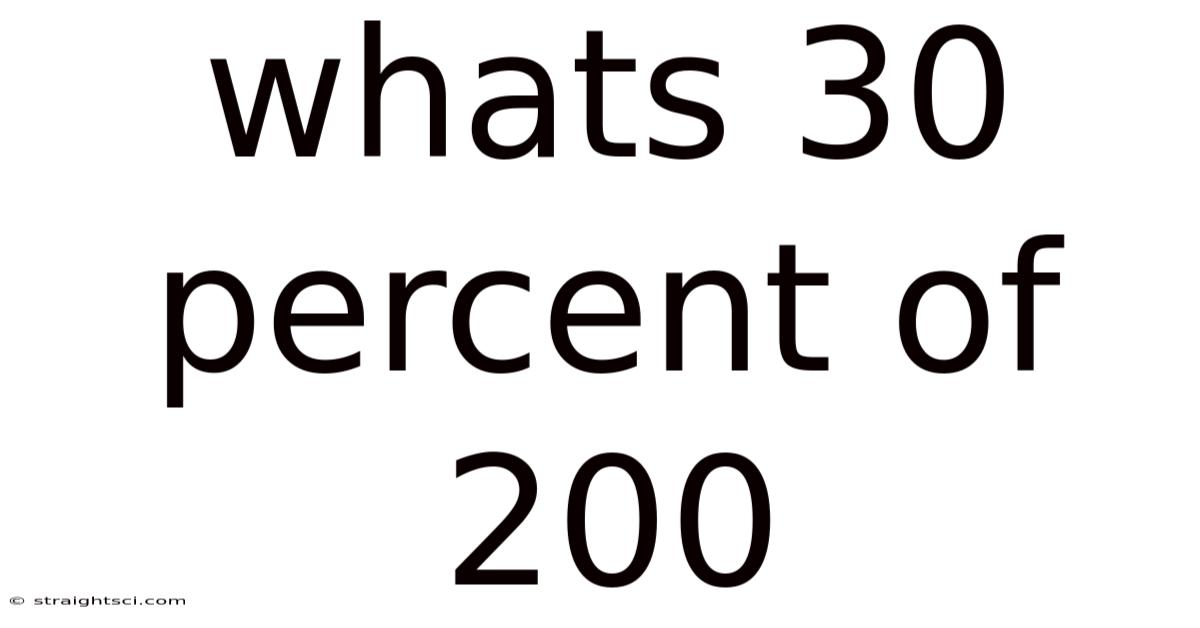
Table of Contents
What's 30 Percent of 200? A Deep Dive into Percentages and Their Applications
Finding 30 percent of 200 might seem like a simple arithmetic problem, quickly solvable with a calculator. However, understanding the underlying concepts of percentages, their calculations, and their broad applications in various fields is far more valuable. This article will not only answer the initial question but also provide a comprehensive exploration of percentages, equipping you with the knowledge to tackle similar problems and understand their significance in real-world scenarios.
Introduction: Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." Therefore, 30% means 30 out of 100, or 30/100, which simplifies to 3/10. This fundamental understanding is crucial for grasping percentage calculations. The symbol % represents the percentage.
Percentages are ubiquitously used in various fields, including:
- Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
- Statistics: Representing data in charts and graphs, analyzing surveys, and understanding probabilities.
- Science: Expressing concentrations of solutions, experimental yields, and statistical significance.
- Everyday life: Calculating tips, sales discounts, and understanding nutritional information on food labels.
Calculating 30 Percent of 200: The Three Main Methods
There are several ways to calculate 30 percent of 200. Let's explore three common methods:
Method 1: Using the Fraction Method
As mentioned earlier, 30% is equivalent to 30/100 or 3/10. To find 30% of 200, we can multiply 200 by the fraction 3/10:
(3/10) * 200 = 60
Therefore, 30 percent of 200 is 60.
Method 2: Using Decimal Conversion
Percentages can be easily converted into decimals by dividing the percentage by 100. In this case, 30% becomes 0.30 (or simply 0.3). We then multiply this decimal by 200:
0.3 * 200 = 60
Again, we arrive at the answer: 30 percent of 200 is 60.
Method 3: Using the Proportion Method
This method is particularly useful for solving more complex percentage problems. We set up a proportion:
Let x represent 30% of 200.
x / 200 = 30 / 100
To solve for x, we cross-multiply:
100x = 200 * 30
100x = 6000
x = 6000 / 100
x = 60
Once again, we find that 30 percent of 200 is 60.
Choosing the Right Method
The best method depends on personal preference and the complexity of the problem. The fraction method is straightforward for simple calculations. The decimal method is efficient and widely used, especially with calculators. The proportion method is more versatile and applicable to a wider range of percentage problems.
Beyond the Basics: Solving More Complex Percentage Problems
Now that we've mastered finding 30% of 200, let's explore how to tackle more complex percentage problems. Here are a few examples:
-
Finding the Percentage: If you know the part and the whole, you can calculate the percentage. For example, if 15 out of 50 students passed an exam, what percentage passed? (15/50) * 100 = 30%
-
Finding the Whole: If you know the part and the percentage, you can find the whole. For instance, if 25% of a number is 10, what is the number? We can set up a proportion: 25/100 = 10/x. Solving for x gives us x = 40.
-
Percentage Increase/Decrease: These calculations involve finding the percentage change between two numbers. For example, if a price increases from $50 to $60, the percentage increase is calculated as: [(60-50)/50] * 100 = 20%.
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. It's a crucial concept in finance and requires a slightly more complex formula.
Real-world Applications of Percentages
The applications of percentages extend far beyond simple arithmetic exercises. Consider these examples:
-
Sales and Discounts: Retailers frequently advertise discounts as percentages. A "20% off" sale means you pay 80% of the original price.
-
Taxes: Sales tax, income tax, and other taxes are usually expressed as percentages of income or purchase price.
-
Interest Rates: Banks and financial institutions use percentages to represent interest rates on loans, savings accounts, and credit cards. Understanding these percentages is crucial for making informed financial decisions.
-
Data Analysis: Percentages are essential in statistics for representing data proportionally and drawing meaningful conclusions from datasets. Think of opinion polls, survey results, and market research – all heavily rely on percentage representation.
-
Healthcare: Medical dosages are sometimes expressed as percentages, particularly in intravenous solutions or topical applications. This requires precision and a thorough understanding of percentage calculations.
Frequently Asked Questions (FAQ)
-
Q: What if I need to calculate a percentage of a number that's not a whole number?
A: The same methods apply. Simply multiply the decimal equivalent of the percentage by the number. For example, to find 30% of 205.5, you would calculate 0.3 * 205.5 = 61.65.
-
Q: How can I calculate percentage change over time?
A: Percentage change is calculated as [(New Value - Old Value) / Old Value] * 100. A positive result indicates an increase, while a negative result indicates a decrease.
-
Q: Are there any online tools or calculators to help with percentage calculations?
A: Yes, numerous online calculators are available that can perform various percentage calculations, saving you time and effort. However, understanding the underlying principles is key to applying these tools effectively.
-
Q: What are the common mistakes people make when calculating percentages?
A: Common mistakes include incorrect decimal conversion, misinterpreting the problem statement, and not properly applying the formula for percentage change or compound interest.
Conclusion: Mastering Percentages – A Lifelong Skill
Understanding percentages is not merely an academic exercise; it's a fundamental skill applicable to numerous aspects of life. From managing personal finances to interpreting data and making informed decisions in various professional contexts, the ability to calculate and interpret percentages empowers you to navigate the world more effectively. While finding 30% of 200 might seem trivial at first glance, mastering the underlying concepts opens doors to a deeper understanding of numerical relationships and their pervasive influence in our daily lives. Continue practicing different types of percentage problems to solidify your understanding and build confidence in applying this valuable mathematical skill.
Latest Posts
Latest Posts
-
Explosive Range Of Natural Gas
Sep 23, 2025
-
Is Ch3oh Polar Or Nonpolar
Sep 23, 2025
-
1 4 Cup Divided By 3
Sep 23, 2025
-
Volume Of A Sphere Equation
Sep 23, 2025
-
Mountains In The Canadian Shield
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Whats 30 Percent Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.