What Percent Is 20 25
straightsci
Sep 13, 2025 · 5 min read
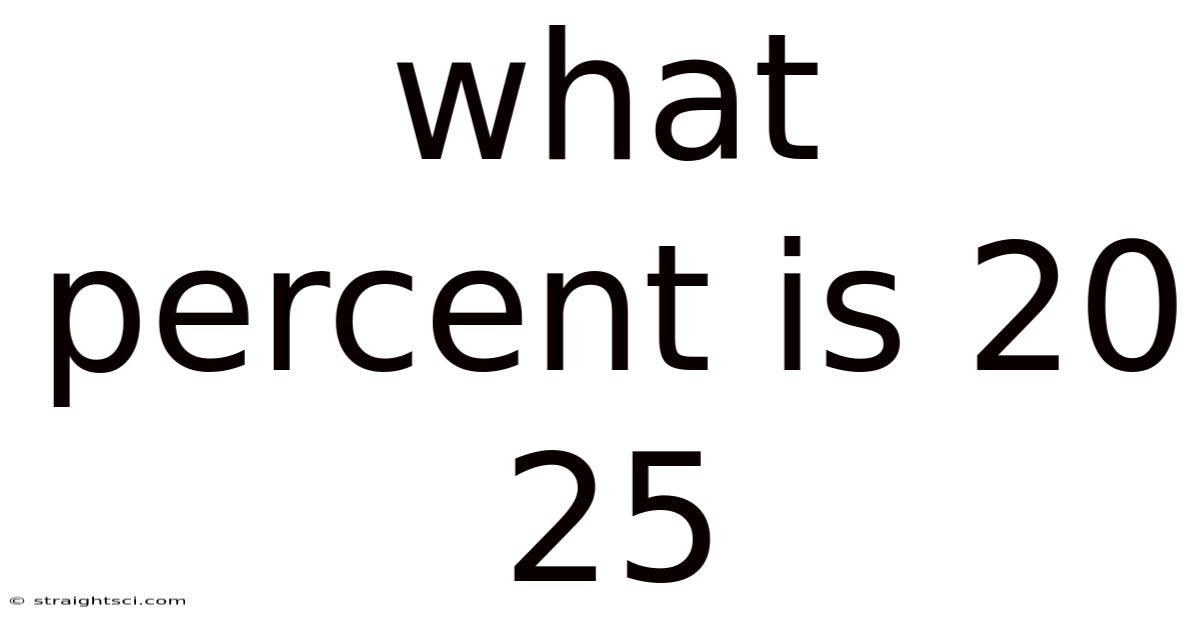
Table of Contents
What Percent is 20 of 25? A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to understanding statistics and financial reports. This article will comprehensively explore the question "What percent is 20 of 25?" We will not only solve this specific problem but also delve into the underlying principles of percentage calculations, providing you with a solid foundation for tackling similar problems independently. We'll cover various methods for solving percentage problems, address common misconceptions, and explore practical examples to illustrate the real-world relevance of this seemingly simple mathematical concept.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a number out of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 50% means 50 out of 100, which can also be written as the fraction 50/100 or the decimal 0.5.
The key to understanding percentages lies in grasping the relationship between three core components:
- The Part: This represents the specific amount we are interested in expressing as a percentage. In our example, "What percent is 20 of 25?", the part is 20.
- The Whole: This is the total amount or the base value to which the part is compared. In our example, the whole is 25.
- The Percentage: This is the value we want to find, representing the part as a proportion of the whole expressed as a number out of 100.
Method 1: Using the Percentage Formula
The most straightforward way to calculate a percentage is using the following formula:
(Part / Whole) x 100% = Percentage
Let's apply this formula to our problem: "What percent is 20 of 25?"
- Part: 20
- Whole: 25
Substituting these values into the formula:
(20 / 25) x 100% = 0.8 x 100% = 80%
Therefore, 20 is 80% of 25.
Method 2: Using Proportions
Another effective method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can express the problem as a proportion:
20/25 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
20 x 100 = 25 x x
2000 = 25x
x = 2000 / 25
x = 80
Therefore, x = 80%, confirming our previous result. This method is particularly useful when dealing with more complex percentage problems.
Method 3: Using Decimal Conversion
We can also solve this by first converting the fraction to a decimal and then multiplying by 100%.
20/25 = 0.8
0.8 x 100% = 80%
Practical Applications: Real-World Examples
Understanding percentages is crucial for navigating various aspects of daily life:
- Shopping: Calculating discounts, sales tax, and comparing prices. For instance, if a $50 item is discounted by 20%, you can use the percentage formula to determine the final price.
- Finance: Understanding interest rates on loans, savings accounts, and investments. Percentages are essential for comprehending compound interest and evaluating investment returns.
- Statistics: Analyzing data and interpreting statistical reports. Percentages are used extensively to represent proportions and trends in data sets.
- Science: Expressing concentrations, yields, and errors in scientific experiments and measurements.
- Everyday Life: Calculating tips in restaurants, understanding nutritional information on food labels, and interpreting survey results.
Common Misconceptions about Percentages
Several common misconceptions can lead to errors in percentage calculations:
- Confusing Part and Whole: It is crucial to correctly identify the part and the whole in a problem. Incorrectly assigning these values will lead to an incorrect percentage.
- Incorrect Decimal Placement: When converting between decimals and percentages, it's easy to misplace the decimal point. Remember to multiply by 100% when converting from a decimal to a percentage and divide by 100% when converting from a percentage to a decimal.
- Percentage Increase vs. Percentage Decrease: Understanding the difference between percentage increase (adding a percentage to a value) and percentage decrease (subtracting a percentage from a value) is essential for accurate calculations.
Beyond the Basics: More Complex Percentage Problems
While our example focuses on a relatively simple percentage calculation, the principles discussed can be applied to more complex scenarios. For instance:
- Calculating percentage change: Finding the percentage increase or decrease between two values. This involves finding the difference between the two values, dividing by the original value, and then multiplying by 100%.
- Calculating percentage points: This refers to the arithmetic difference between two percentages, not a percentage change. For example, an increase from 10% to 15% is a 5 percentage point increase, but a 50% increase in the percentage itself.
- Solving problems involving multiple percentages: These often require breaking the problem down into smaller, manageable steps. For example, calculating a final price after applying multiple discounts.
Frequently Asked Questions (FAQ)
Q: What if the "part" is larger than the "whole"?
A: If the part is larger than the whole, the resulting percentage will be greater than 100%. This signifies that the part exceeds the whole, which is perfectly acceptable in certain contexts. For instance, if you invested $100 and now have $150, your return is 150% of your initial investment.
Q: Can percentages be negative?
A: Yes, percentages can be negative. A negative percentage typically represents a decrease or loss. For example, a -10% change indicates a 10% decrease.
Q: How do I calculate the percentage of a number?
A: To calculate the percentage of a number, multiply the number by the percentage (expressed as a decimal). For example, to find 20% of 50, you would calculate 50 * 0.20 = 10.
Q: How do I find the original number if I know the percentage and the resulting value?
A: This involves working backward using the percentage formula. If you know the percentage and the final value, you can set up an equation and solve for the original number.
Conclusion
The question "What percent is 20 of 25?" serves as a springboard for understanding the fundamental concept of percentages. While the answer, 80%, is relatively straightforward to obtain, the broader implications of percentage calculations extend far beyond this specific problem. By mastering the various methods presented here, from the basic percentage formula to utilizing proportions and decimal conversions, you'll equip yourself with a powerful tool applicable to countless situations in your personal and professional life. Remember that consistent practice is key to developing fluency in percentage calculations, allowing you to confidently tackle more complex problems and apply this crucial mathematical skill with accuracy and ease.
Latest Posts
Latest Posts
-
Century Is How Many Years
Sep 13, 2025
-
Sq Ft In Quarter Acre
Sep 13, 2025
-
25 Oz Yeast To Tsp
Sep 13, 2025
-
How To Calculate Deadweight Loss
Sep 13, 2025
-
Enveloped Vs Non Enveloped Virus
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 20 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.