What Is Half Of 2/3
straightsci
Sep 19, 2025 · 5 min read
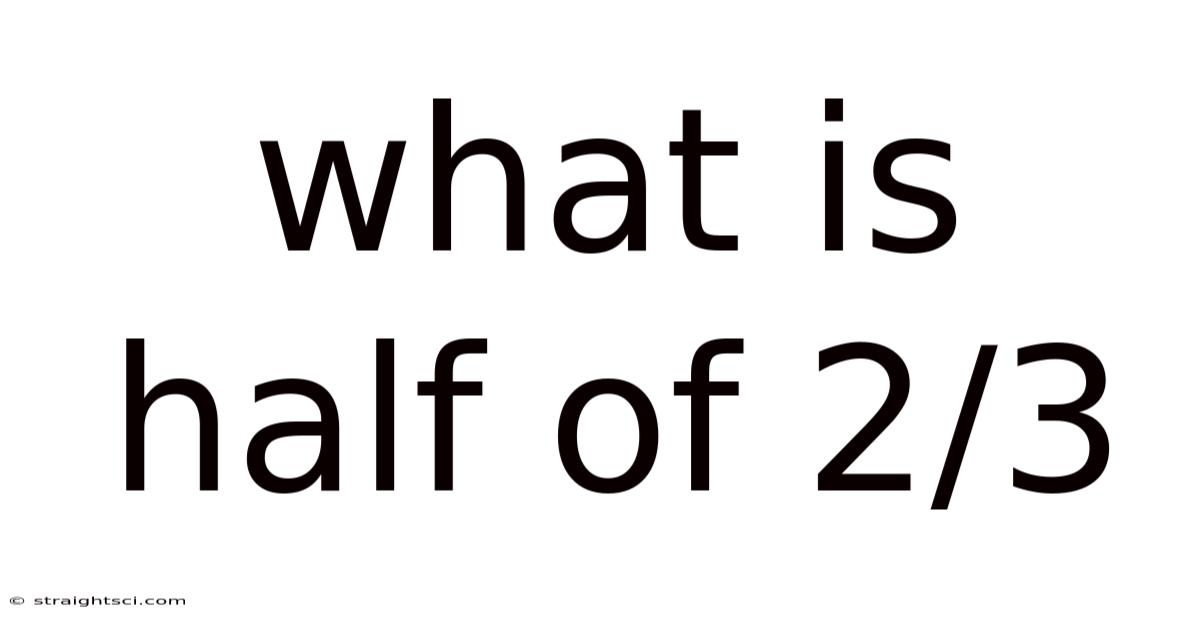
Table of Contents
What is Half of 2/3? A Deep Dive into Fractions and Division
Finding half of 2/3 might seem like a simple arithmetic problem, but it's a great opportunity to explore the fundamental concepts of fractions, division, and how these operations interact. This article will not only provide the answer but also delve into the underlying mathematical principles, offering a comprehensive understanding suitable for learners of all levels. We'll cover various approaches to solving the problem, address common misconceptions, and even explore real-world applications.
Introduction: Understanding Fractions
Before we tackle the problem of finding half of 2/3, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 2/3, the numerator is 2 and the denominator is 3. This means we have 2 parts out of a total of 3 equal parts.
Method 1: Multiplying by 1/2
Finding half of a number is equivalent to multiplying that number by 1/2. Therefore, to find half of 2/3, we simply multiply 2/3 by 1/2:
(2/3) * (1/2) = (2 * 1) / (3 * 2) = 2/6
This fraction, 2/6, can be simplified. Both the numerator and the denominator are divisible by 2:
2/6 = 1/3
Therefore, half of 2/3 is 1/3.
Method 2: Dividing by 2
Alternatively, we can interpret "half of 2/3" as dividing 2/3 by 2. When dividing fractions, we invert the second fraction (the divisor) and multiply:
(2/3) / 2 = (2/3) * (1/2) = 2/6 = 1/3
This method confirms our previous result: half of 2/3 is 1/3.
Method 3: Visual Representation
Visualizing the problem can enhance understanding. Imagine a circle divided into three equal parts. The fraction 2/3 represents two of these three parts. To find half of 2/3, we divide those two parts in half. Each of the original three parts is now divided into two smaller parts, resulting in six smaller parts in total. We initially had two of the three larger parts, which now translates to four of the six smaller parts. This represents the fraction 4/6, which simplifies to 1/3.
Method 4: Decimal Conversion
We can also solve this problem using decimal representation. First, convert the fraction 2/3 into a decimal:
2/3 ≈ 0.6667 (approximately)
Then, find half of this decimal value:
0.6667 / 2 ≈ 0.3333 (approximately)
Converting this back to a fraction gives us approximately 1/3. Note that the decimal representation introduces a slight approximation due to the recurring decimal nature of 2/3.
Explanation of the Mathematical Principles
The core mathematical principles at play here involve the operations of multiplication and division with fractions. Multiplication of fractions involves multiplying the numerators together and the denominators together. Division of fractions involves inverting the divisor (the fraction you're dividing by) and then multiplying. Simplifying fractions involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD. This process reduces the fraction to its simplest form, making it easier to understand and compare.
Common Misconceptions
A common misconception is to simply halve the numerator: taking half of 2 to get 1, leaving the denominator unchanged (resulting in 1/3). While this happens to give the correct answer in this specific case, it's not a generally applicable method. This approach is incorrect for fractions other than those with a numerator that is an even number. The correct approach involves multiplying by 1/2 or dividing by 2, as explained in the methods above.
Real-World Applications
Understanding fractions and operations with them is crucial in various real-world scenarios. Here are a few examples:
- Cooking and Baking: Recipes often involve fractions of ingredients. Knowing how to halve or double a recipe requires understanding fraction manipulation.
- Construction and Engineering: Precise measurements in construction and engineering rely on fractions and decimals. Calculating the dimensions of materials frequently involves fraction arithmetic.
- Finance: Calculating interest rates, discounts, and proportions of investments all involve fraction and decimal calculations.
- Data Analysis: Representing and interpreting data often involves fractions and percentages, which are related to fractions.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this? A: Yes, a calculator can be used to convert the fractions to decimals and perform the division. However, understanding the underlying mathematical principles is essential for broader application.
-
Q: What if the fraction was different, like 1/3? A: Finding half of 1/3 would involve multiplying (1/3) * (1/2) = 1/6.
-
Q: Is there another way to visualize this problem? A: Yes, you can use a rectangular model. Divide a rectangle into three equal parts. Shade two parts to represent 2/3. Then, divide the shaded area in half. You'll see that this represents 1/3 of the original rectangle.
-
Q: Why is simplifying fractions important? A: Simplifying fractions helps in making comparisons and calculations easier. For example, understanding that 2/6 is equivalent to 1/3 makes it easier to compare the relative sizes of these fractions.
Conclusion: Mastering Fractions for a Brighter Future
Finding half of 2/3, while seemingly simple, provides a valuable opportunity to reinforce and deepen our understanding of fractions and their manipulation. By exploring different methods and visualizing the problem, we gain a more intuitive and robust grasp of these concepts. Mastering fraction arithmetic is a fundamental skill with widespread applicability across various fields, equipping us to tackle more complex mathematical challenges and real-world situations with confidence and precision. Remember that consistent practice and a focus on understanding the underlying principles are key to building a strong mathematical foundation. Don’t be afraid to explore different methods and visualize the problem; this will solidify your comprehension and boost your mathematical skills. The ability to easily manipulate fractions is a skill that will serve you well throughout your life.
Latest Posts
Latest Posts
-
Finding Area Of A Circle
Sep 19, 2025
-
Is Propane Heavier Than Air
Sep 19, 2025
-
10 Ml To Cc Syringe
Sep 19, 2025
-
Most Populated States In Us
Sep 19, 2025
-
Adv Healthcare Materials Impact Factor
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.