What Is 80 Of 15
straightsci
Sep 06, 2025 · 6 min read
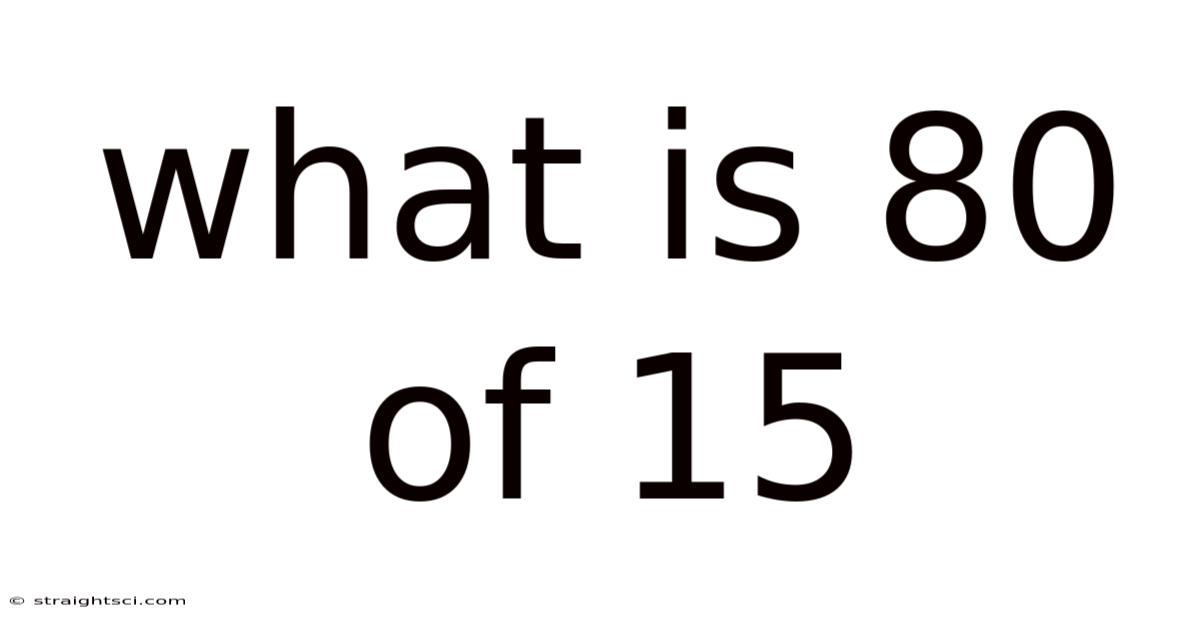
Table of Contents
What is 80% of 15? A Deep Dive into Percentages and Practical Applications
Finding 80% of 15 might seem like a simple calculation, but it opens the door to understanding a fundamental mathematical concept: percentages. This article will not only show you how to calculate 80% of 15 but also delve into the underlying principles, explore different calculation methods, and illustrate practical applications of percentage calculations in everyday life. Understanding percentages is crucial for various fields, from finance and budgeting to sales and statistics. This comprehensive guide will equip you with the knowledge and skills to confidently tackle percentage problems of any complexity.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The word "percent" literally means "out of one hundred" ( per cent). So, 80% means 80 out of 100, which can be written as a fraction (80/100) or a decimal (0.8). This fundamental understanding is key to solving percentage problems.
Calculating 80% of 15: Three Methods
There are several ways to calculate 80% of 15. Let's explore three common methods:
Method 1: Using the Fraction Method
This method involves converting the percentage to a fraction and then multiplying it by the number.
-
Step 1: Convert the percentage to a fraction: 80% is equivalent to 80/100, which simplifies to 4/5.
-
Step 2: Multiply the fraction by the number: (4/5) * 15 = 60/5
-
Step 3: Simplify the fraction: 60/5 = 12
Therefore, 80% of 15 is 12.
Method 2: Using the Decimal Method
This method involves converting the percentage to a decimal and then multiplying it by the number.
-
Step 1: Convert the percentage to a decimal: 80% is equivalent to 0.8 (move the decimal point two places to the left).
-
Step 2: Multiply the decimal by the number: 0.8 * 15 = 12
Therefore, 80% of 15 is 12.
Method 3: Using Proportions
This method sets up a proportion to solve for the unknown value.
-
Step 1: Set up the proportion: 80/100 = x/15 (where x represents 80% of 15)
-
Step 2: Cross-multiply: 80 * 15 = 100 * x
-
Step 3: Solve for x: 1200 = 100x => x = 1200/100 = 12
Therefore, 80% of 15 is 12.
Why These Methods Work: A Deeper Look
All three methods are essentially different ways of expressing the same underlying mathematical principle. They all involve finding a part of a whole. The percentage represents the part we are interested in, and the total number (15 in this case) represents the whole.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in many real-world situations. Here are some examples:
-
Sales and Discounts: Calculating discounts on items during sales. For example, a 20% discount on a $50 item.
-
Taxes: Determining the amount of tax to be paid on purchases or income. Sales tax, income tax, and property tax all involve percentage calculations.
-
Interest Rates: Calculating interest earned on savings accounts or interest paid on loans. Understanding compound interest, which involves repeated percentage calculations, is crucial for financial planning.
-
Tips and Gratuities: Calculating tips in restaurants or gratuities for services.
-
Statistics and Data Analysis: Percentages are widely used to represent data in graphs, charts, and reports. For example, representing the percentage of people who prefer a certain product or the percentage change in a company's profits.
-
Finance and Budgeting: Tracking expenses, creating budgets, and managing personal finances often involve percentage calculations. For instance, determining what percentage of your income goes towards rent or food.
-
Science and Engineering: Percentages are used to express concentrations, efficiencies, and error margins in various scientific and engineering applications.
Beyond the Basics: More Complex Percentage Problems
While calculating 80% of 15 is relatively straightforward, percentage problems can become more complex. Here are some examples:
-
Finding the percentage: If you know the part and the whole, you can find the percentage. For example, if 3 out of 5 apples are red, what percentage of apples are red? (3/5)*100 = 60%
-
Finding the whole: If you know the part and the percentage, you can find the whole. For example, if 20% of a number is 10, what is the number? 10 / 0.20 = 50
-
Percentage increase/decrease: Calculating the percentage change between two numbers. For example, if a price increases from $10 to $12, what is the percentage increase? [(12-10)/10]*100 = 20%
-
Compound interest: Calculating interest earned on an investment over multiple periods, where the interest earned is added to the principal amount each period.
Frequently Asked Questions (FAQ)
Q1: How do I calculate a percentage of a number quickly in my head?
A1: For simple percentages like 10%, 20%, 50%, etc., mental math is often easiest. For 10%, move the decimal point one place to the left. For 20%, double the 10% value. For 50%, divide the number by 2. For other percentages, you can often break them down into simpler percentages. For example, 15% can be calculated as 10% + 5% (5% is half of 10%).
Q2: Are there any online calculators or tools to help with percentage calculations?
A2: Yes, many online calculators and spreadsheet programs (like Microsoft Excel or Google Sheets) have built-in functions for percentage calculations. These tools can be very helpful for more complex problems.
Q3: What if the number I'm finding the percentage of is a decimal or fraction?
A3: The methods described earlier still apply. Simply convert the decimal or fraction to a decimal before multiplying by the percentage (expressed as a decimal).
Q4: How can I improve my skills in percentage calculations?
A4: Practice is key. Start with simple problems and gradually work your way up to more complex ones. Using online resources, workbooks, and practice tests can help you build your skills and confidence.
Conclusion: Mastering Percentages for a Brighter Future
Calculating 80% of 15, while seemingly trivial, serves as a springboard to understanding the broader world of percentages. This fundamental concept has far-reaching implications across numerous disciplines and everyday scenarios. By mastering the different methods of percentage calculation and understanding their practical applications, you equip yourself with a valuable skill that will enhance your problem-solving abilities and empower you to navigate the complexities of the modern world with confidence. Remember that consistent practice and a willingness to explore different approaches are essential to building a strong foundation in this critical mathematical area. The ability to confidently work with percentages isn't just about solving equations; it's about developing a deeper understanding of proportional relationships and their pervasive role in our daily lives.
Latest Posts
Latest Posts
-
How Many Lbs Is 24oz
Sep 07, 2025
-
Protons Neutrons Electrons Of Nitrogen
Sep 07, 2025
-
Sum Of Infinite Geometric Series
Sep 07, 2025
-
How Much Is 3 8 Inches
Sep 07, 2025
-
3 X 5 X 2
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about What Is 80 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.