What Is 70 Of 20
straightsci
Sep 13, 2025 · 5 min read
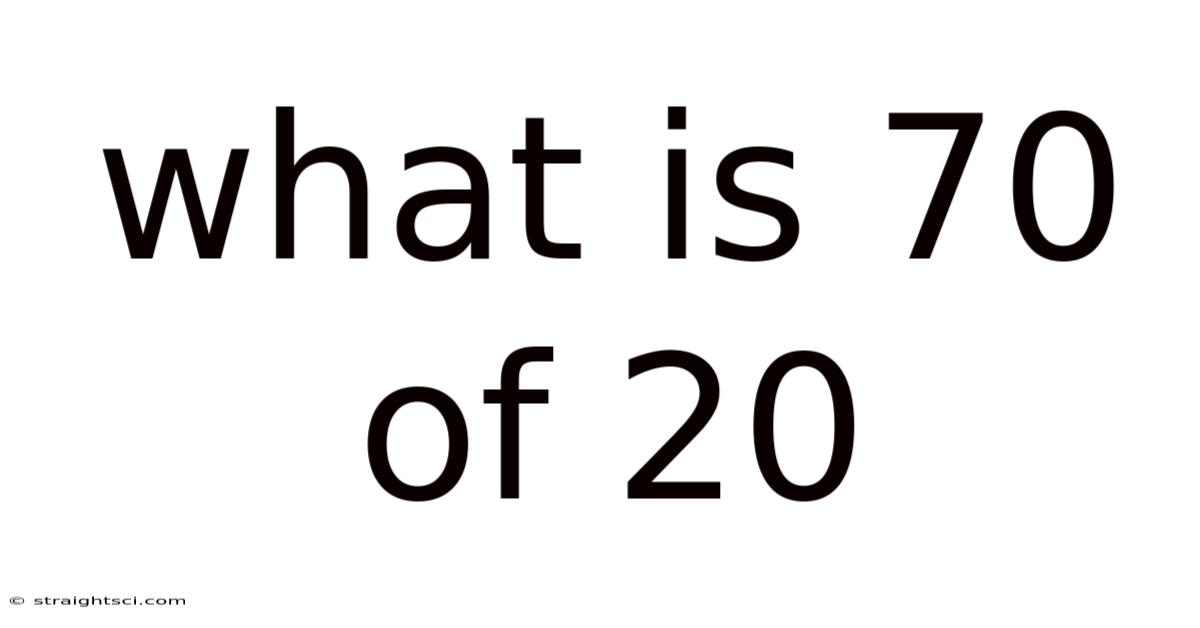
Table of Contents
What is 70% of 20? A Deep Dive into Percentages and Their Applications
Finding 70% of 20 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding how to calculate percentages, and more importantly, the underlying concepts, is crucial for various aspects of life, from managing finances to understanding statistics and interpreting data in many fields. This article will not only show you how to calculate 70% of 20 but will also delve deeper into the world of percentages, explaining the methods, providing real-world examples, and addressing frequently asked questions.
Understanding Percentages: The Basics
A percentage is a fraction or a ratio expressed as a number out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of one hundred." Therefore, 70% means 70 out of 100, which can be written as the fraction 70/100 or the decimal 0.7. Understanding this fundamental concept is key to solving any percentage problem.
Calculating 70% of 20: Three Methods
There are several ways to calculate 70% of 20. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. We know that 70% is equivalent to 0.7. To find 70% of 20, we simply multiply 20 by 0.7:
20 * 0.7 = 14
Therefore, 70% of 20 is 14.
Method 2: Using Fractions
As mentioned earlier, 70% can be expressed as the fraction 70/100. To find 70% of 20, we multiply 20 by 70/100:
20 * (70/100) = (20 * 70) / 100 = 1400 / 100 = 14
Again, we arrive at the answer: 14. This method is particularly useful when dealing with more complex percentages or fractions. Simplifying the fraction before multiplying can often make the calculation easier. For example, 70/100 simplifies to 7/10.
Method 3: Using Proportions
This method is more conceptual and helps solidify the understanding of percentages. We can set up a proportion:
70/100 = x/20
Where 'x' represents the unknown value (70% of 20). To solve for x, we cross-multiply:
70 * 20 = 100 * x
1400 = 100x
x = 1400 / 100 = 14
This method clearly shows the relationship between the percentage, the whole, and the part. It's a valuable method for visualizing the problem and understanding the underlying principle.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous real-world situations. Here are a few examples:
-
Sales and Discounts: Imagine a store offering a 70% discount on a $20 item. Using the methods above, we know the discount is $14, and the final price would be $6 ($20 - $14). This is a common application encountered daily by consumers.
-
Taxes and Interest: Calculating taxes on income or interest accrued on savings accounts involves percentage calculations. Understanding these calculations is vital for effective financial planning and budgeting.
-
Statistical Analysis: Percentages are ubiquitous in data analysis and statistics. Representing data as percentages allows for easier comparison and interpretation of trends and patterns. For example, expressing the percentage of students who passed an exam provides a clearer picture than simply stating the raw number of students who passed.
-
Scientific Research: Many scientific fields, such as biology, chemistry, and medicine, use percentages to represent concentrations, yields, and other important data.
Beyond the Basics: Advanced Percentage Calculations
While finding 70% of 20 is relatively simple, more complex percentage problems might require additional steps. For instance:
-
Finding the percentage one number represents of another: If you scored 14 out of 20 on a test, what percentage did you achieve? This involves dividing the obtained score (14) by the total score (20) and multiplying by 100: (14/20) * 100 = 70%.
-
Finding the original amount after a percentage increase or decrease: If a price increased by 20% to reach $24, what was the original price? This requires working backward using algebraic equations.
-
Calculating compound interest: Compound interest involves calculating interest on both the principal amount and accumulated interest. This requires more advanced formulas and understanding of exponential growth.
Frequently Asked Questions (FAQs)
Q: What if I need to calculate a percentage that's not a whole number, such as 70.5% of 20?
A: The methods remain the same. Simply use the decimal equivalent (0.705) and multiply by 20. The calculation would be 20 * 0.705 = 14.1.
Q: Are there any shortcuts for calculating percentages mentally?
A: Yes, for certain percentages, mental shortcuts exist. For instance, 10% of a number is simply that number divided by 10. 5% is half of 10%, and so on. These shortcuts become more intuitive with practice.
Q: What are some common percentage mistakes to avoid?
A: A common mistake is confusing percentage increase with percentage points. For example, an increase from 10% to 20% is a 10 percentage point increase, but a 100% increase in the percentage itself. Another common mistake is incorrectly calculating percentage changes over multiple periods. It's crucial to understand the difference between simple and compound interest, or percentage changes.
Q: What tools can help with percentage calculations?
A: Besides calculators, many online tools and software programs are available to assist with percentage calculations. Spreadsheet programs like Microsoft Excel and Google Sheets have built-in functions for calculating percentages.
Conclusion
Calculating 70% of 20, while seemingly elementary, provides a gateway to understanding a fundamental concept that permeates numerous aspects of life. Mastering percentage calculations, from the basic methods to more advanced applications, is crucial for academic success, financial literacy, and effective data interpretation in various professional fields. By understanding the underlying principles and practicing the different calculation methods, you'll not only be able to solve percentage problems but also develop a stronger analytical and problem-solving skillset. Remember to practice regularly and utilize the various resources available to enhance your understanding and proficiency in working with percentages.
Latest Posts
Latest Posts
-
Is Nacl Ionic Or Covalent
Sep 14, 2025
-
Buffer Zone On Titration Curve
Sep 14, 2025
-
Vertex Formula For Quadratic Equation
Sep 14, 2025
-
What Is A Polyatomic Compound
Sep 14, 2025
-
Capitalist Economy Advantages And Disadvantages
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 70 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.