What Is 30 Of 300
straightsci
Sep 20, 2025 · 5 min read
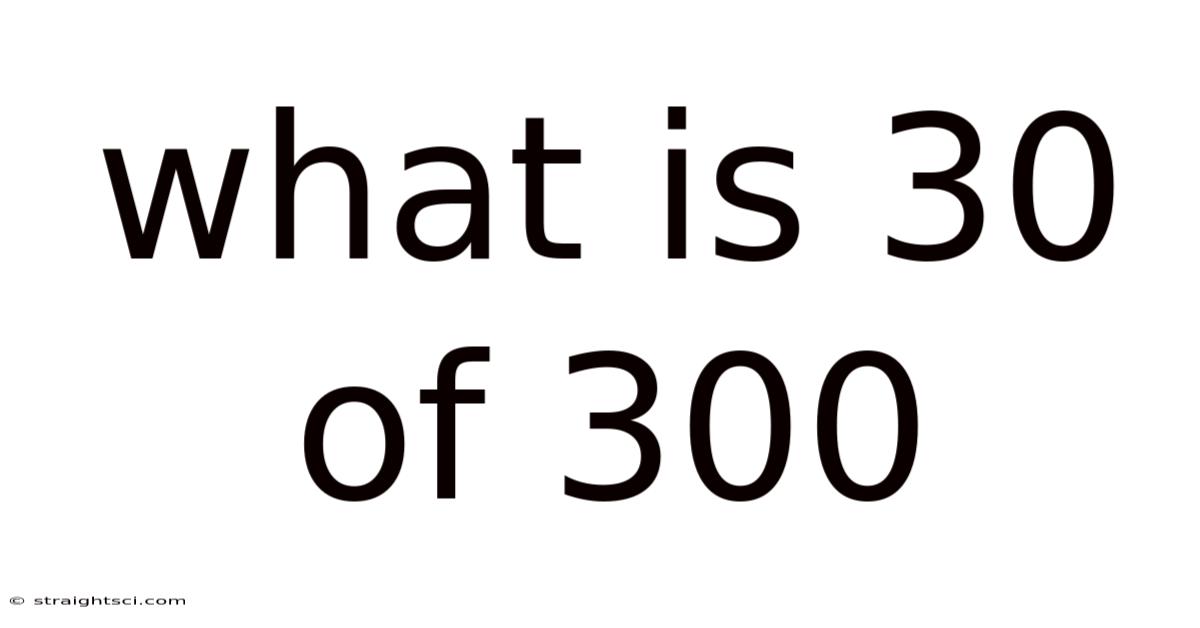
Table of Contents
What is 30 of 300? Understanding Fractions, Percentages, and Ratios
Finding out "what is 30 of 300?" might seem like a simple math problem, but it's a gateway to understanding fundamental concepts in mathematics like fractions, percentages, and ratios. These concepts are crucial not only in academic settings but also in everyday life – from calculating discounts to understanding financial reports. This article will delve into various ways to solve this problem, explaining the underlying principles and expanding on their applications.
Understanding the Problem: 30 of 300
The phrase "30 of 300" essentially asks us to determine the relationship between the number 30 and the number 300. We can interpret this question in several ways, each leading to a different but equally valid answer. The most common interpretations involve fractions, percentages, and ratios. Let's explore each one.
Method 1: Expressing it as a Fraction
The most straightforward approach is to represent the relationship as a fraction. The question "What is 30 of 300?" can be translated into the fraction 30/300. This fraction signifies that 30 is a part of a larger whole, 300. To simplify this fraction, we find the greatest common divisor (GCD) of 30 and 300, which is 30. Dividing both the numerator and the denominator by 30, we get:
30/300 = 1/10
Therefore, 30 is one-tenth of 300. This fraction represents the proportional relationship between the two numbers. It means that for every 10 parts, 1 part is equivalent to 30, and the whole is 300.
Method 2: Calculating the Percentage
Percentages are another effective way to express the relationship between 30 and 300. A percentage shows the proportion of a number relative to 100. To calculate the percentage, we use the following formula:
(Part / Whole) * 100%
In this case, the part is 30, and the whole is 300. Plugging these values into the formula:
(30 / 300) * 100% = 0.1 * 100% = 10%
Therefore, 30 is 10% of 300. This representation is commonly used in everyday contexts, making it easy to understand the proportional relationship at a glance.
Method 3: Defining it as a Ratio
A ratio expresses the relationship between two numbers, showing how much of one quantity there is for every unit of another. The ratio of 30 to 300 can be written as 30:300 or 30/300. Similar to the fraction, we can simplify this ratio by dividing both numbers by their GCD (30):
30:300 simplifies to 1:10
This ratio indicates that for every 1 unit of the first quantity, there are 10 units of the second quantity. Ratios are frequently used in situations comparing different quantities, such as comparing ingredients in a recipe or analyzing proportions in various fields like chemistry or finance.
Expanding the Concepts: Real-World Applications
Understanding fractions, percentages, and ratios extends far beyond simple calculations. Let's explore some practical applications:
-
Financial Calculations: Calculating interest rates, discounts, profit margins, and tax rates all involve these concepts. For instance, a 10% discount on a $300 item translates to a $30 discount ($300 * 0.10 = $30).
-
Data Analysis: Representing data using percentages and ratios provides a clearer picture of proportions and trends. In market research, percentages might show the market share of different brands, while ratios could compare sales figures across different regions.
-
Recipe Scaling: Adjusting recipes to serve more or fewer people requires understanding proportions and ratios. If a recipe calls for 30 grams of flour for 300 grams of dough, you can scale it down or up using the 1:10 ratio.
-
Probability and Statistics: These fields heavily rely on fractions and percentages to express the likelihood of events occurring. The probability of selecting a specific item from a set of items is often represented as a fraction.
-
Scientific Measurements and Conversions: Converting units, expressing concentrations, and many other scientific calculations rely on understanding ratios and proportions.
Beyond the Basics: Further Exploration
While the solution to "What is 30 of 300?" is relatively straightforward, understanding the underlying concepts allows for more complex problem-solving. Here are some further explorations:
-
Inverse Proportions: Exploring inverse relationships helps understand situations where an increase in one quantity leads to a decrease in another. For example, if it takes 30 workers 300 hours to complete a project, how long would it take 60 workers?
-
Compound Percentages: Understanding how percentages accumulate over time is essential in areas like finance (compound interest) and population growth.
-
Proportional Reasoning: Developing strong proportional reasoning skills enhances problem-solving abilities across various disciplines, enabling you to efficiently tackle more complex challenges involving ratios and proportions.
Frequently Asked Questions (FAQ)
Q1: What is the difference between a fraction, a percentage, and a ratio?
A1: While all three represent proportions, they differ in their expression:
-
Fraction: Represents a part of a whole, expressed as a numerator over a denominator (e.g., 1/10).
-
Percentage: Represents a proportion relative to 100, denoted by the % symbol (e.g., 10%).
-
Ratio: Represents the relative size of two or more values, often expressed using a colon (e.g., 1:10) or a fraction.
Q2: How can I improve my understanding of fractions, percentages, and ratios?
A2: Practice is key! Solve various problems involving these concepts, starting with simple examples and gradually moving towards more complex ones. Utilize online resources, textbooks, and educational videos to strengthen your understanding.
Q3: Are there any online tools or calculators that can help with these calculations?
A3: While this article avoids linking to external sites, many free online calculators are available that can perform fraction, percentage, and ratio calculations. Search online for "fraction calculator," "percentage calculator," or "ratio calculator" to find these resources.
Conclusion: Mastering Fundamental Mathematical Concepts
Determining "what is 30 of 300?" isn't just about getting a numerical answer (1/10, 10%, or 1:10). It's about grasping fundamental concepts – fractions, percentages, and ratios – that are essential tools for navigating various aspects of life. By understanding these concepts and their applications, you equip yourself with valuable skills applicable to numerous fields, enhancing your problem-solving capabilities and overall comprehension of quantitative information. Consistent practice and a deeper exploration of related mathematical principles will further solidify your understanding and unlock the power of these fundamental tools.
Latest Posts
Latest Posts
-
Stem Of Dicot And Monocot
Sep 21, 2025
-
Base Si Unit For Mass
Sep 21, 2025
-
Sentence With The Word Arbitrary
Sep 21, 2025
-
Food Chains And Food Webs
Sep 21, 2025
-
Sugar Maple Tree Scientific Name
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 300 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.